Week 4 Stationary/Standing Waves

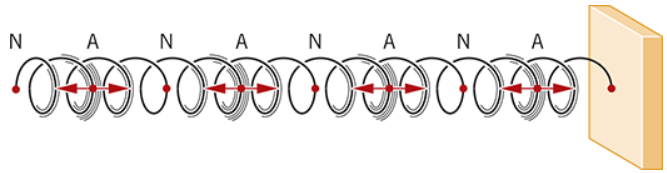
stationary/standing wave

wave patterns formed by the interference of two waves with the same frequency and amplitude traveling in opposite directions, storing energy without transfering it; has nodes and antinodes

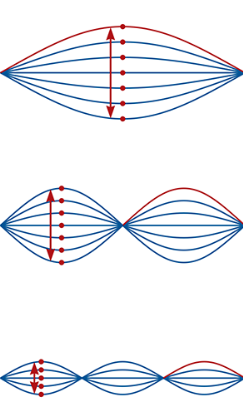
antinode

maximum vibration of the stationary wave

node

zeero vibration of the stationary wave

harmonic wave

a wave with a frequency that’s an integer multiple of the frequency of the original (fundamental) wave; harmonic number corresponds to the # of loops in the standng wave pattern

fundamental frequency

lowest frequency in the series, aka first harmonic

overtone

any resonant frequency above the fundamental frequency (ex. second harmonic is called first overtone)

first overtone is also

second harmonic

equation to find the fundamental frequency of standing wave

f1 = v/wavelength = 1/2L x v = 1/2L x sqrt(T/linear density)

where v = speed, L = length of string, and T = tension force

equation to find wavelength of nth harmonic on a string

wavelengthn = 2L/n

equation to find frequency of nth harmonic on a string

fn = v/wavelength = n x v/2L = n/2L x sqrt(T/linear density) = n x f1(fundamental frequency)

equation to find harmonic frequency for stationary wave on string

harmonic frequency = # of ½ wavelenths x fundamental frequency

resonance

phenomenon where an ocillating system (ex. sound wave) absorbs max energy and vibrates with significantly larger amplitude because the frequency of a periodically applied force is equal or close to the medium’s natural frequency

natural frequency

any frequency an object vibrates when disturbed (determinedby its mass and stiffness), fundamental frequency is the lowest of the natural frequencies

comparing standing and progressive waves

frequency: stationary wave all particles except at the nodes are at the same frequency - progressive wave all particles vibrates at the same frequency

amplitude: stationary wave amplitude varies from 0 @ nodes & max @ antinodes - progressive waves amplitude is the same for all particles

phase difference b/w 2 particles: stationary waves equal to mπ where m = # b/w 2 particles - progressive waves equal to 2πd/wavelength wehre d=distance apart

principle of linear superposition

when two or more waves are present simultaneously at the same place, the resultant disturbance is the sume of the disturbances from the individual waves. can be applied to all types of waves

condensation in waves

also means compression in longitudinal waves

closed pipes and waves

pipes with one side closed and one side open must have node at closed end and an antinode at the open end