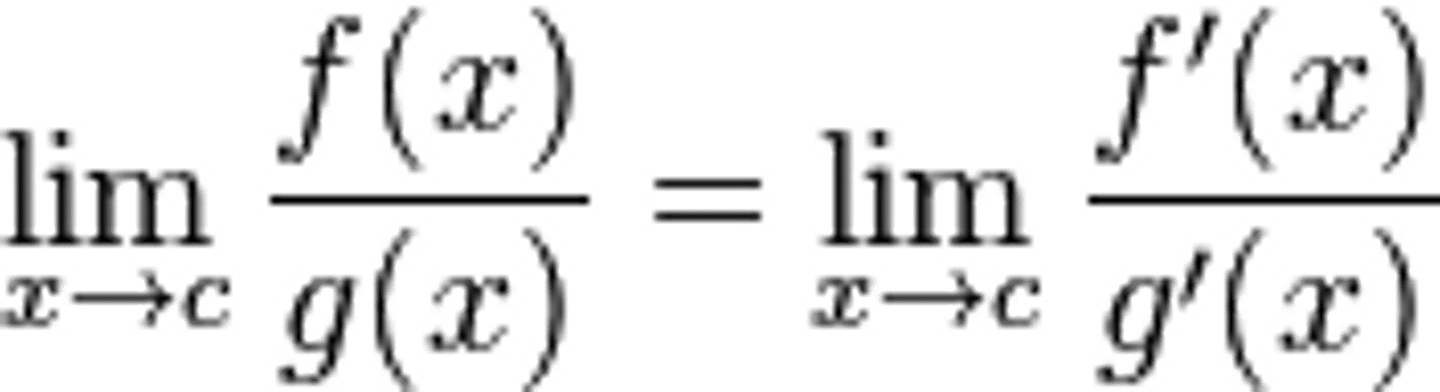AP Calc All Cards

antiderivative of sinx

-cos x + C

antiderivatie of cosx

sin x + c

antiderivative of tanx

-ln|cosx|+c

antiderivative of cotx

ln|sinx| + C

antiderivative of secx

ln|secx + tanx| + C

antiderivative of cscx

-ln|cscx+cotx| + C

antiderivative of a^x

a^x/ln(a) + C

derivative of arcsinx

u'/√(1-u^2)

derivative of arctanx

u'/(1 + u^2)

derivative of arcsecx

u'/(|u|√(u^2-1))

du/√(a^2-u^2)

arcsin u/a + c

du/a^2+u^2

(1/a)arctan(u/a)+C

du/u√u^2-a^2

(1/a)arcsec(|u|/a) + C

derivative of a^x

a^x ln(a)

derivative of log base a time x

1/lna times x

limit as x approaches 0: sinx/x

1

Intermediate Value Theorem

If f is continuous on [a,b] and k is a number between f(a) and f(b), then there exists at least one number c such that f(c)=k

Removable vs Non-removable Discontinuity

Removable: hole

Limit Definition of Derivative At A Point

limit where x approaches c: f(x)-f(c)/x-c

Limit Definition

lim h->0 = f(x+h)-f(x)/h

Power Rule

d/dx x^n = nx^n-1

Product Rule

f'(x)g(x)+f(x)g'(x)

Quotient Rule

g(x)f'(x)-f(x)g'(x)/g(x)^2

f(x)=sinx

f'(x)=cosx

f(x)=cosx

f'(x)=-sinx

f(x)=tanx

f'(x)=sec^2(x)

f(x)=cotx

f'(x)=-csc^2x

f(x)=secx

f'(x)=secxtanx

f(x)=cscx

f'(x)=-cscxcotx

Chain Rule

f'(g(x))g'(x)

Critical Numbers

X-values where f' is zero or undefined

First Derivative Test

Used to determine where a function's graph has a min/max and is increasing or decreasing.

Second Derivative Test

Used to determine on what intervals a function is concave up/concave down and the points of inflections.

Mean Value Theorem

f'(c) = (f(b) - f(a))/ (b - a)

Rolle's Theorem

if f(x) is continuous on [a,b] and differentiable on (a,b), and if f(a)=f(b), then there is at least one point (x=c) on (a,b) [DON'T INCLUDE END POINTS] where f'(c)=0

y=lnu

y'=(1/u)*u'

y=a^x

y'=a^x*lna

y=logax

y'=1/xlna

The sum of i

n(n+1)/2

The sum of i^2

n(n+1)(2n+1)/6

The sum of i^3

n^2(n+1)^2/4

Limit at infinity when the degree of numerator is less than denominator

The limit at infinity is 0.

Limit at infinity when the degree of numerator is equal to denominator

the ratio of the leading coefficients

Limit at infinity when the degree of numerator is more than denominator

The limit at infinity is either positive or negative infinity, depending on the signs of the leading coefficients and whether the limit is at positive or negative infinity.

Derivative of e^x

e^x

Derivative of lnx

1/x

Slope of tangent or secant line

rise over run

Derivative of f'(c) when f(x) is an inverse of g(x)

1/g'(f(c))

L'Hôpital's rule