Physics Midterm (copy)

A. 1 m/s
B. 5 m/s

C. 7 m/s

D. 12 m/s

C

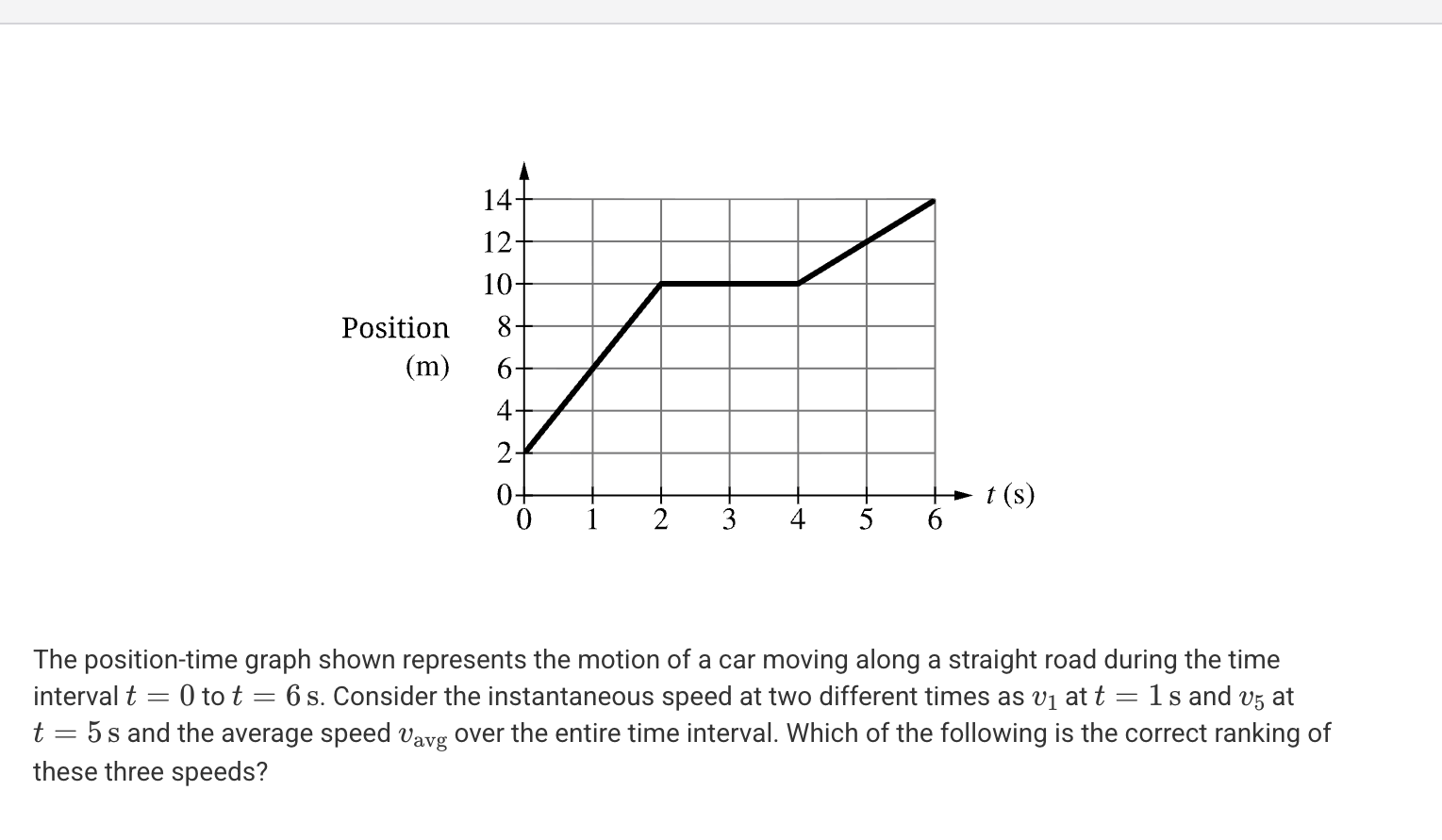
A. v₁ < v_avg < v₅

B. v₅ = v_avg < v₁

C. v_avg < v₅ < v₁

D. v_avg < v₅ = v₁

B

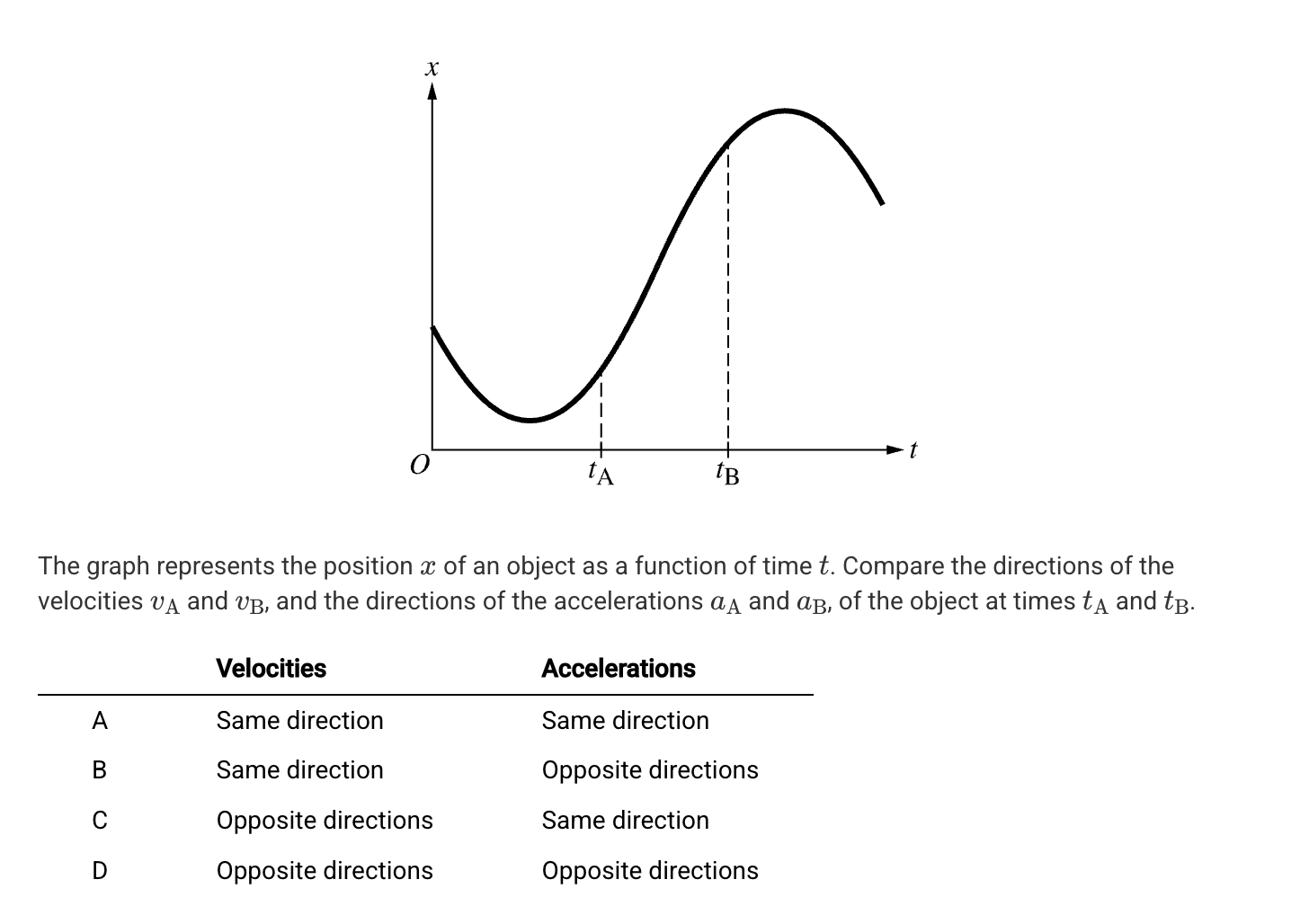
A. No because x ≥ 0 at any given time.

B. No because the acceleration is constant and nonzero.

C. Yes because the object is located at the origin at t = 3s.

D. Yes because the velocity of the object changes sign at t = 3s.

D

B

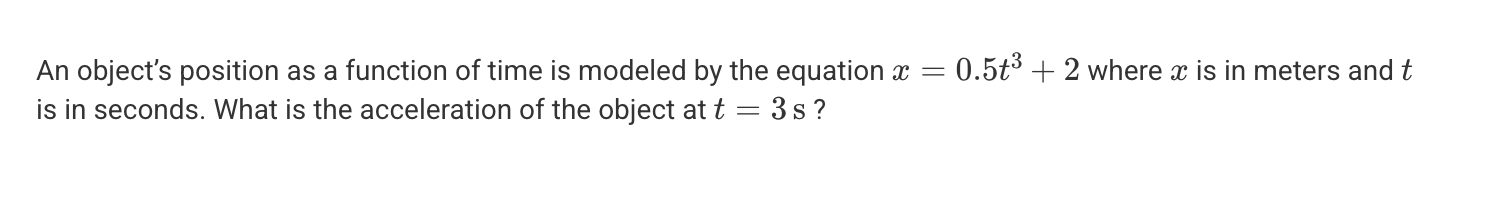
A. 3.0 m/s²

B. 9.0 m/s²

C. 13.5 m/s²

D. 15.0 m/s²

B

A. 21 cm/s

B. 31 cm/s

C. 84 cm/s

D. 136 cm/s

B

A. The student’s equation does not account for the initial position of the object.

B. The student’s equation does not account for the initial velocity of the object.

C. The student’s equation does not substitute a = 3t in the 1/2at² term.

D. The student’s equation should not have a +1 term, as integrating the acceleration function twice yields x=1/2t³.

B

A. a_A/2

B. a_A

C. 2a_A

D. 4a_A

C

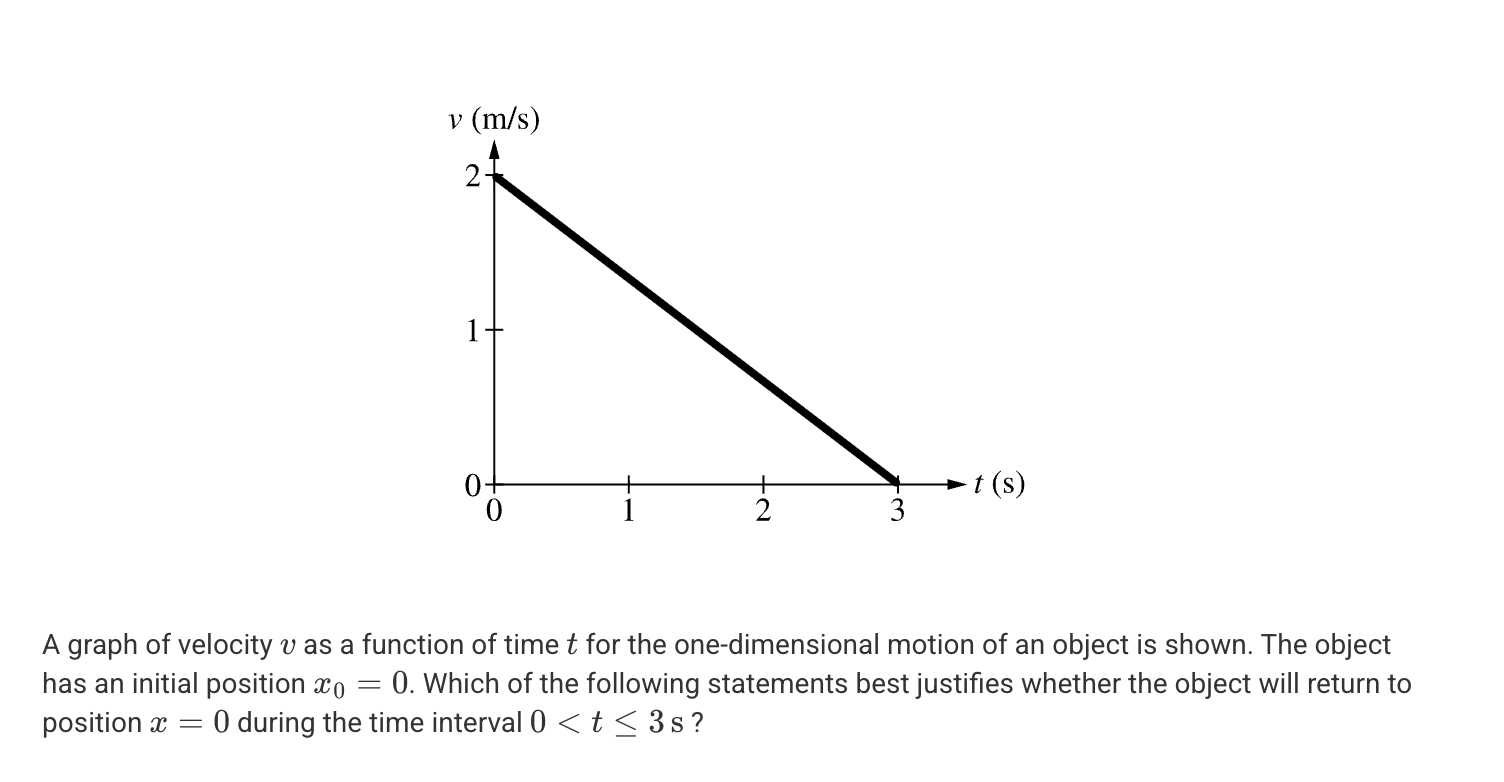
A. No, because the distance between the object and its initial position is increasing during the entire time interval.

B. No, because the object has a constant acceleration during this time interval.

C. Yes, because the velocity of the object is zero at t = 3 s.

D. Yes, because the acceleration of the object is negative during this time interval.

A

A. The car has a positive initial velocity and a negative acceleration because the position values are positive and are decreasing.

B. The car has a positive initial velocity and a negative acceleration because the position is decreasing and the magnitude of displacement in each time interval increases.

C. The car has a negative initial velocity and a negative acceleration because the position values are positive and are decreasing.

D. The car has a negative initial velocity and a negative acceleration because the position is decreasing and the magnitude of displacement in each time interval increases.

D

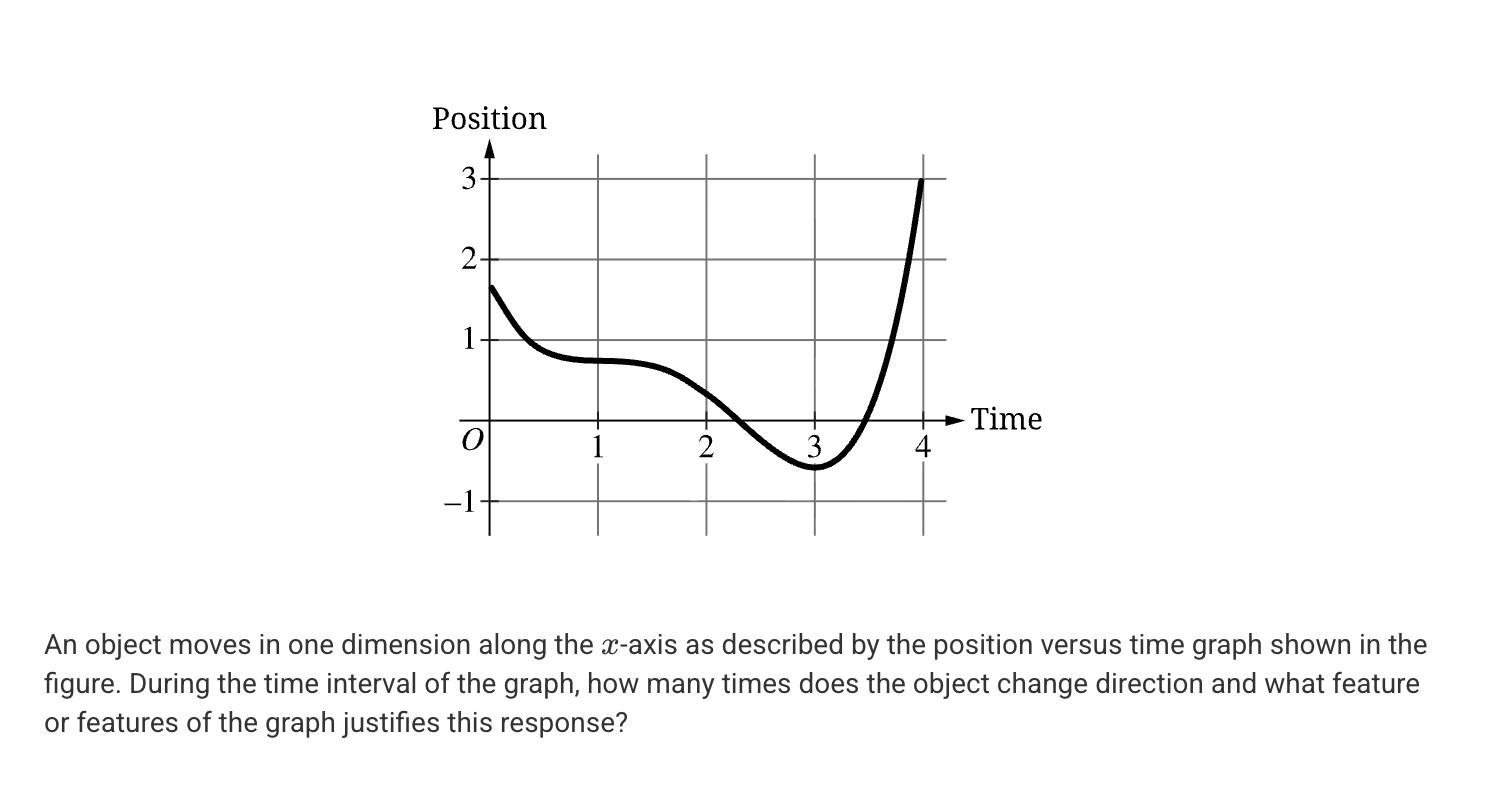
A. One time because the graph indicates that there is a single point where the object’s velocity is zero and its acceleration is zero.

B. One time because the graph indicates that there is a single point where the object’s velocity is zero and its acceleration is nonzero.

C. Two times because the graph indicates that the velocity of the object is zero at two different points.

D. Two times because the graph indicates that the position of the object is zero at two different points.

B

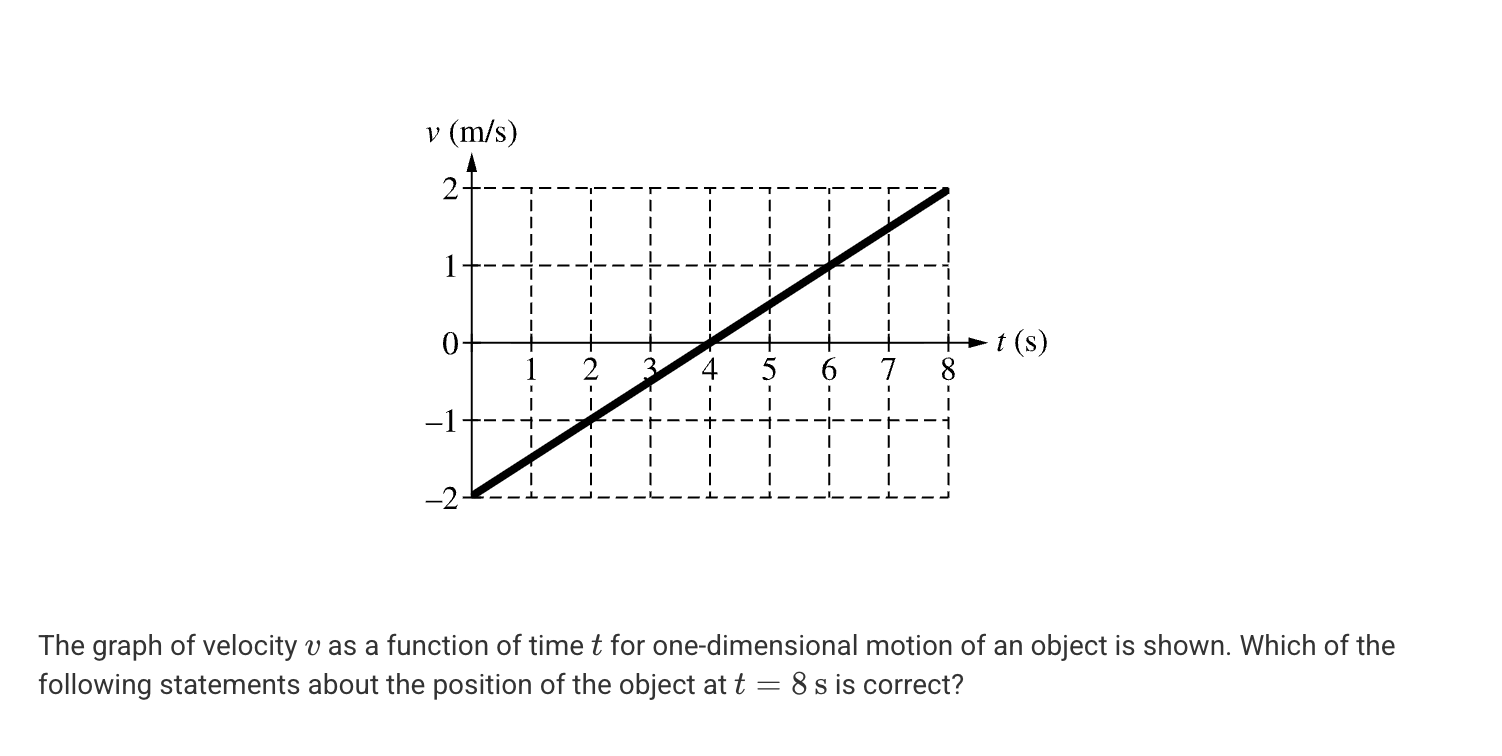
A. The position of the object is 4 m, because the object moves from -2 m to +2 m during the entire time interval.

B. The position of the object is 4 m, because the area under the velocity graph is 4 m during the time interval when v is positive.

C. The position of the object is the same as its position at t = 0, because the velocity is zero exactly halfway through the time interval.

D. The position of the object is the same as its position at t = 0, because the area under the velocity graph is zero for the entire time interval.

D

A. t_p/16

B. t_p/4

C. 4t_p

D. 16t_p

C

A. 1/6 gt_f

B. ¼gt_f

C. 2/3 gt_f

D. 7/6 gt_f

A

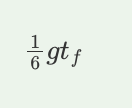
A. 2 Δx/t

B. Δx/t

C. 2/3 Δx/t

D. ½ Δx/t

A

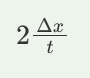
A. 9d

B. 3d

C. d/3

D. d/9

C

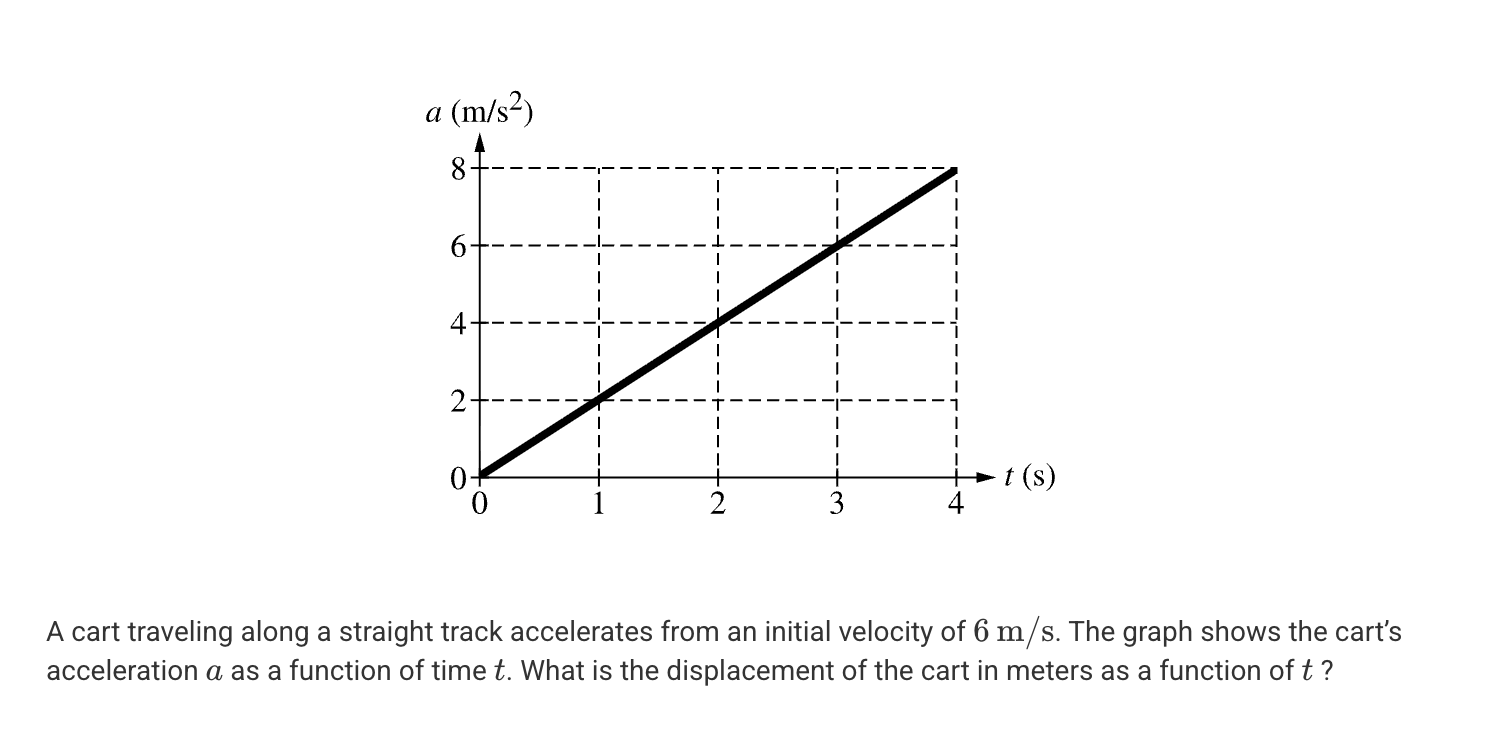
A. 0

B. 1/3 t³

C. 4t² + 6t

D. 1/3 t³ + 6t

D

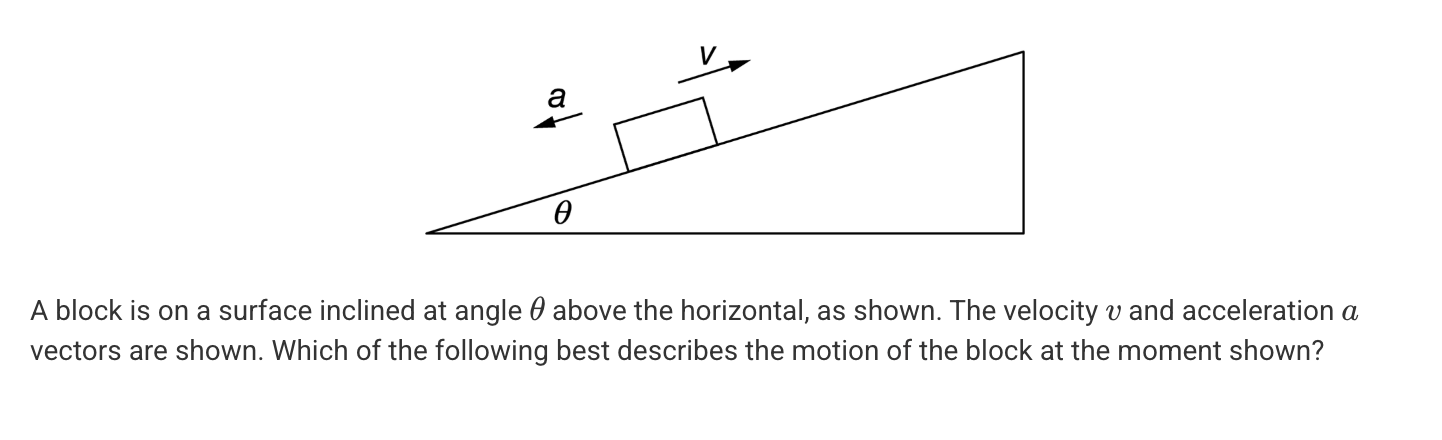
A. The block is moving up the incline and speeding up.

B. The block is moving up the incline and slowing down.

C. The block is moving down the incline and speeding up.

D. The block is moving down the incline at a constant speed.

E. The block is moving down the incline and slowing down.

B

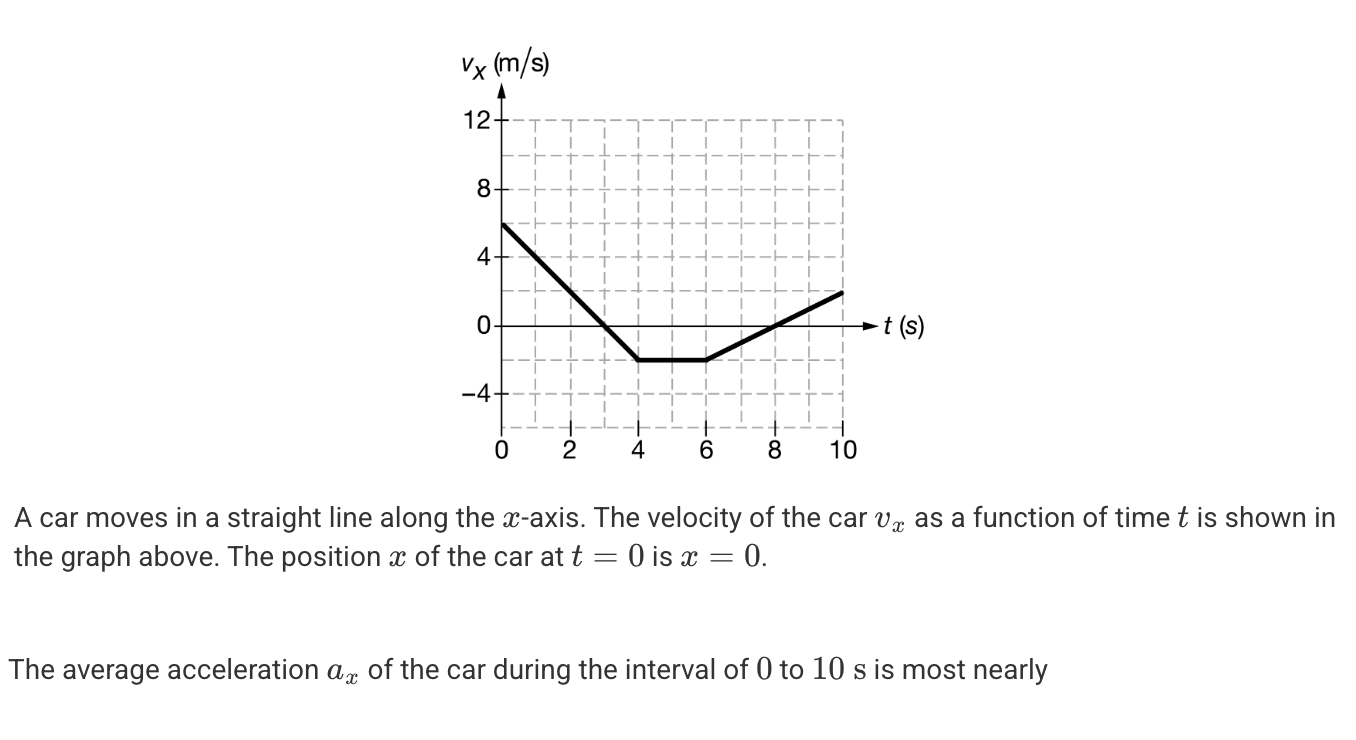
A. -2.0 m/s²

B. -0.40 m/s²

C. +0.40 m/s²

D. +1.0 m/s²

E. +2.0 m/s²

B

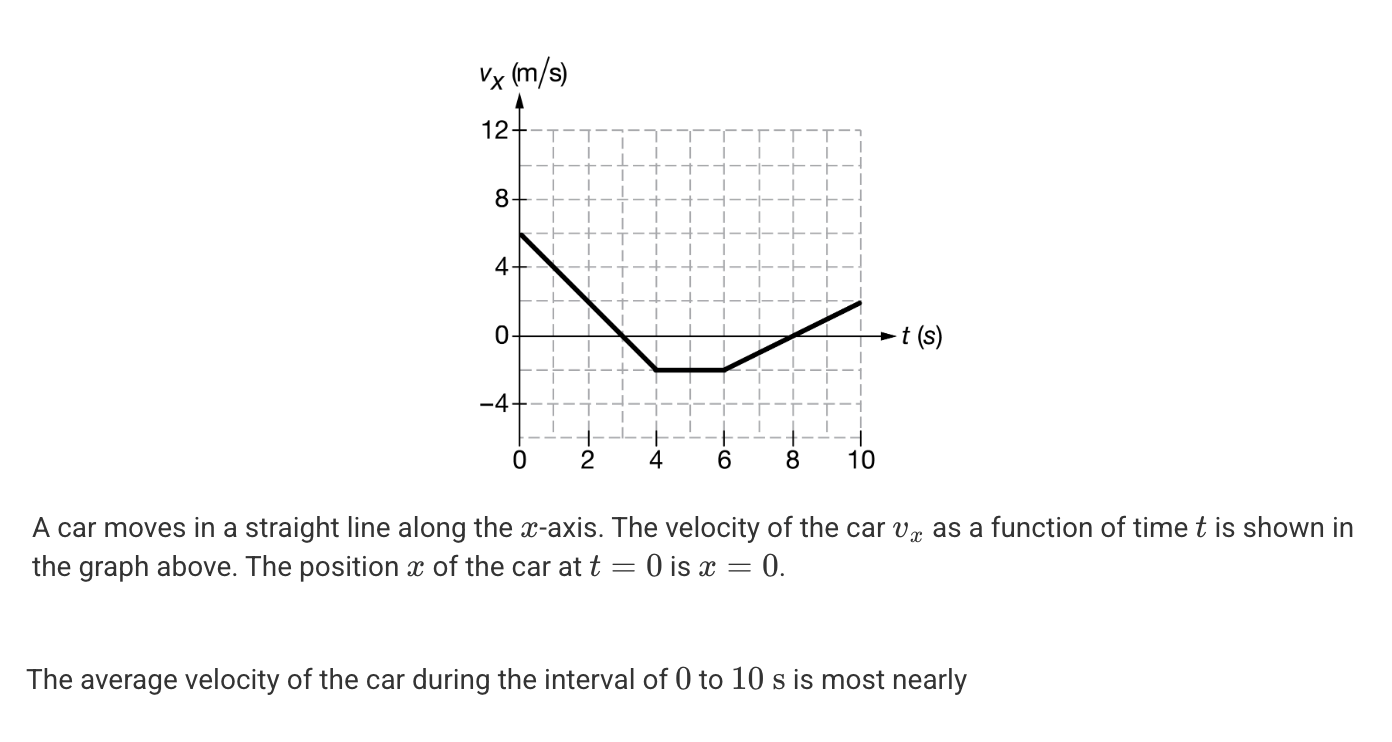
A. -1.4 m/s

B. +0.40 m/s

C. +1.4 m/s

D. +1.8 m/s

E. +4.0 m/s

B

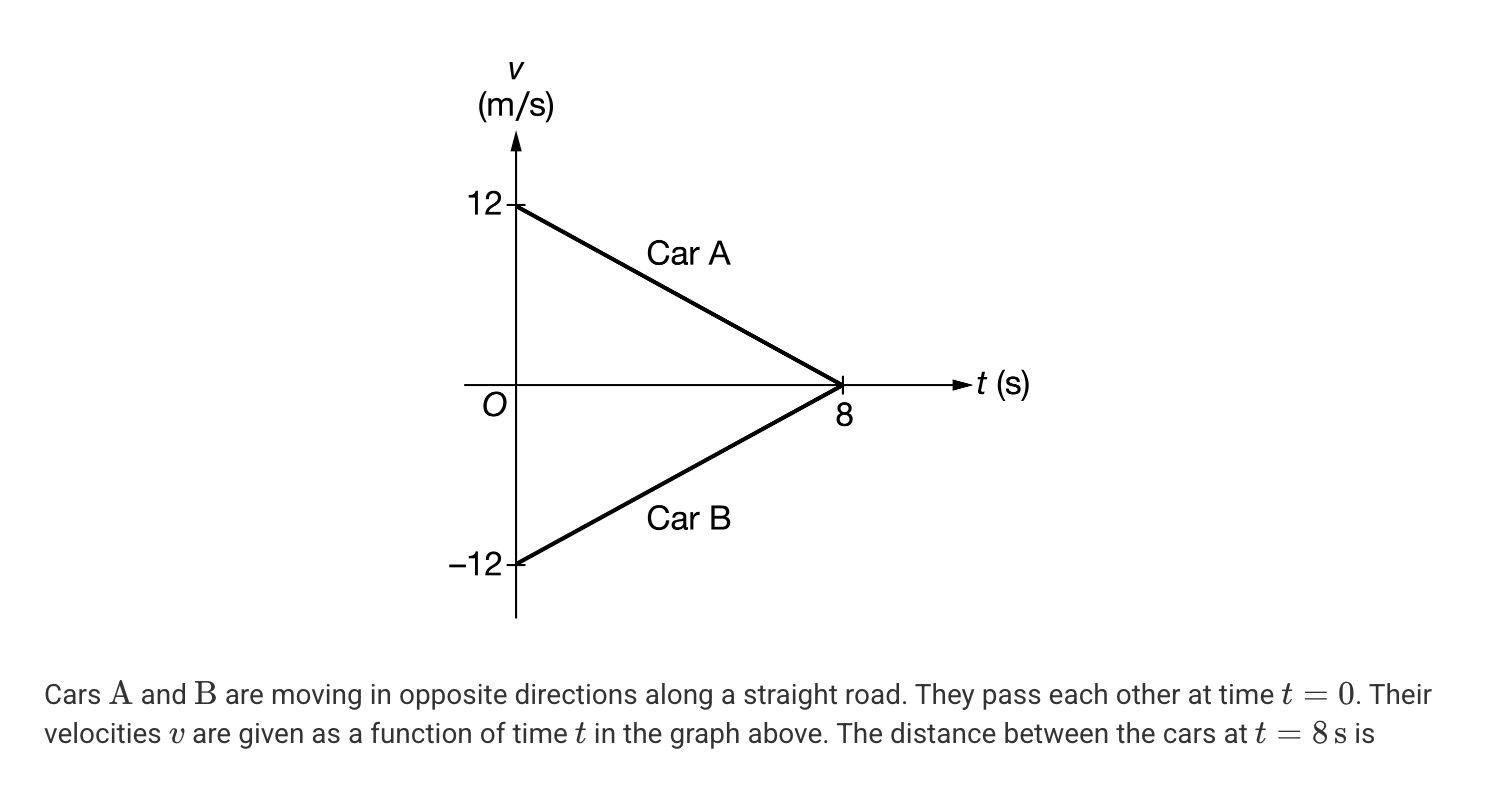
A. Zero

B. 24 m

C. 48 m

D. 96 m

E. 192 m

D

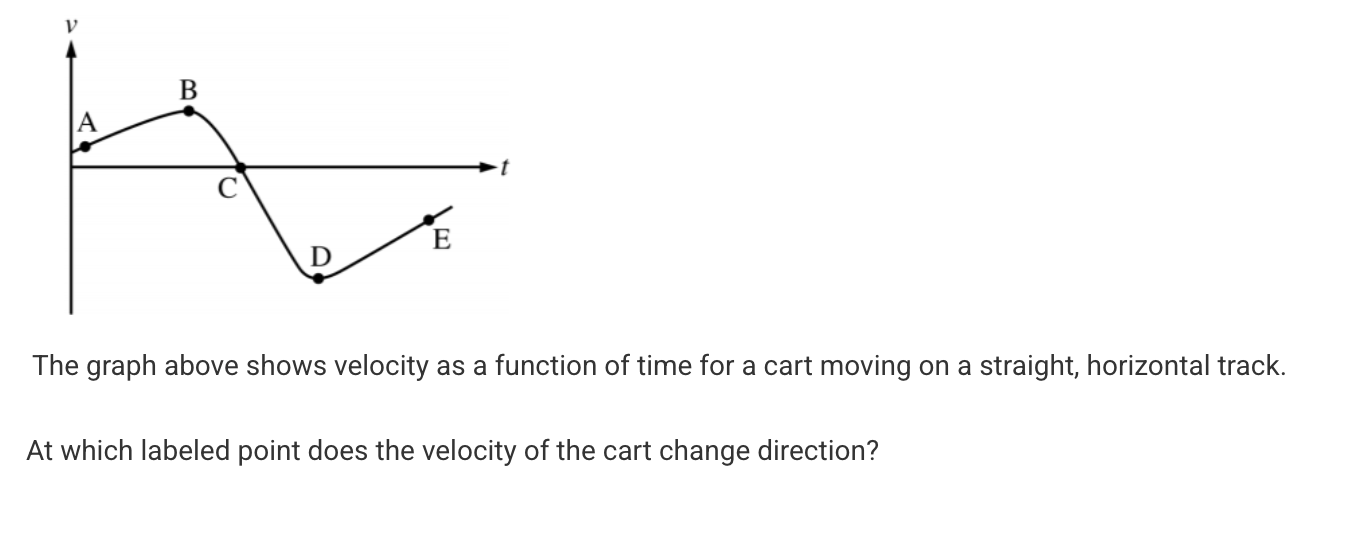
A

B

C

D

E

C

A. d/4

B. d/2

C. d

D. 2d

E. 4d

E

A. Speed: Decreasing, Direction of Motion: Positive

B. Speed: Increasing, Direction of Motion: Positive

C. Speed: Constant, Direction of Motion: Positive

D. Speed: Decreasing, Direction of Motion: Negative

E. Speed: Increasing, Direction of Motion: Negative

A

A. v(t) = d/dt (2t³ - 3t² - 8t - 3) = 0

B. v(t) = d/dt (2t³ - 3t² - 8t - 3)

C. v(t) = ∫ (2t³ - 3t² - 8t - 3) dx

D. v(t) = ∫ (2t³ - 3t² - 8t - 3) dt

E. v(t) = (2t³ - 3t² - 8t - 3)/t

B

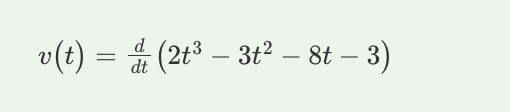
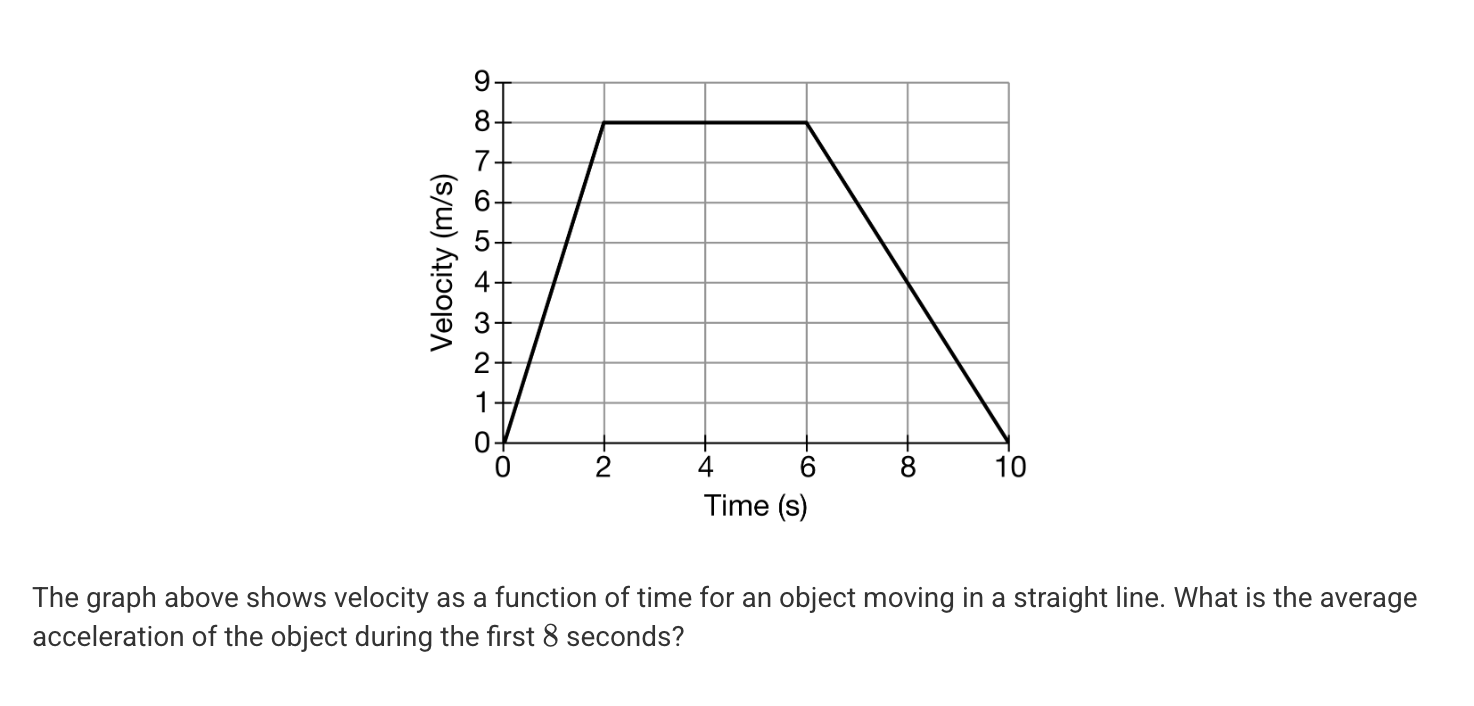
A. -2.0 m/s²

B. -0.5 m/s²

C. 0 m/s²

D. +0.5 m/s²

E. +2.0 m/s²

D

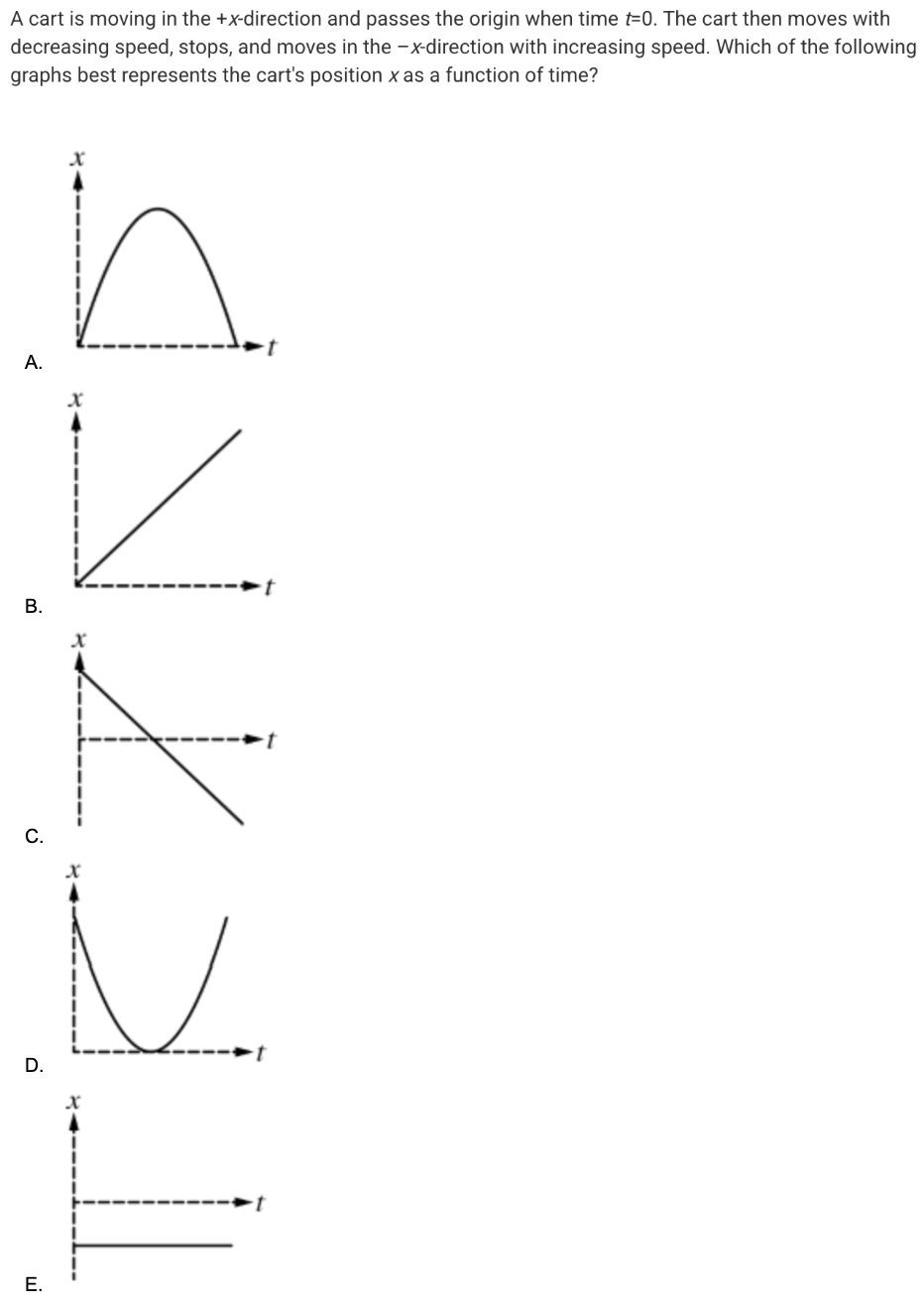
A.

B.

C.

D.

E.

A

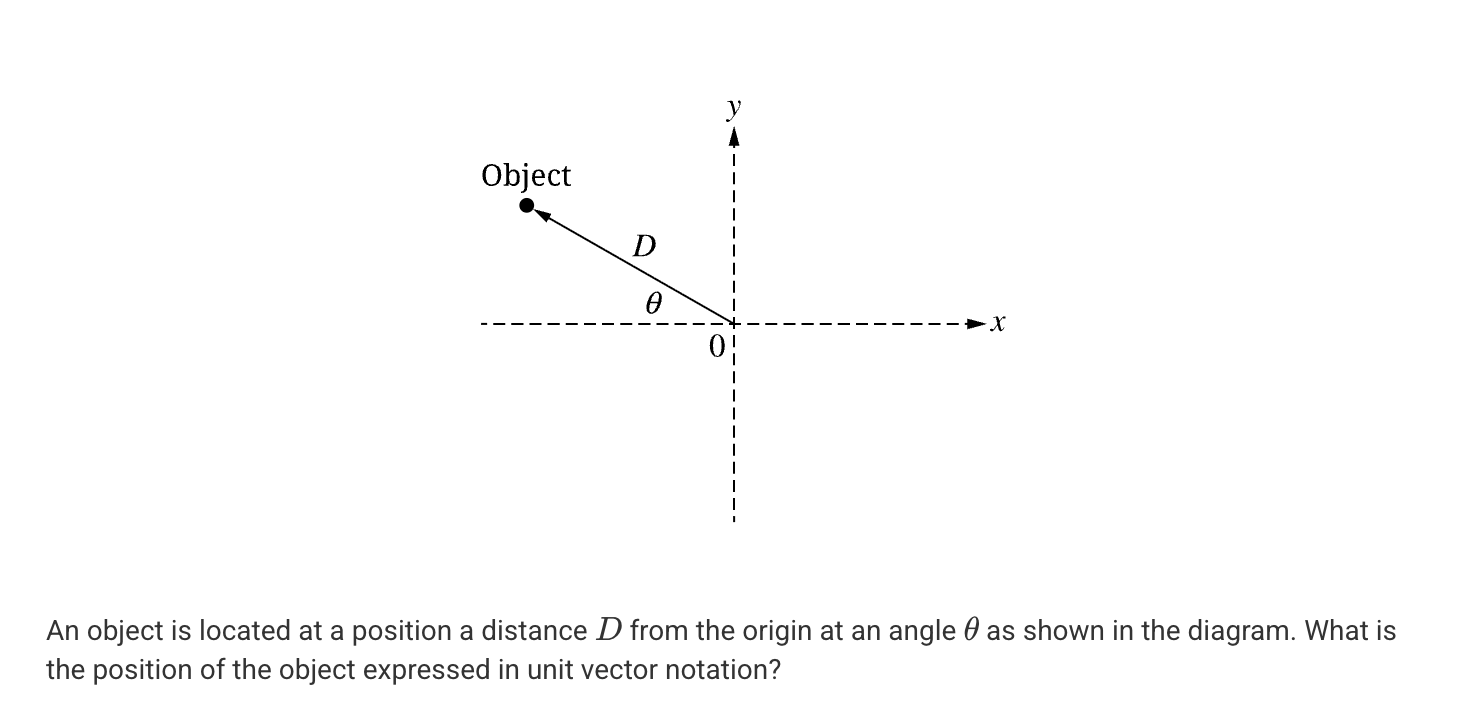
A. -Dcosθî + Dsinθĵ

B.Dcosθî - Dsinθĵ

C. -Dsinθî + Dcosθĵ

D. Dsinθî - Dcosθĵ

A

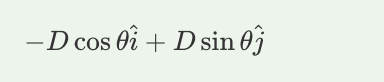
A. 5 m/s² at 53° above the +x-direction

B. 5 m/s² at 53° above the -x-direction

C. 1 m/s² in the +x-direction

D. 1 m/s² in the -x-direction

B

A. y = -4

B. y = -1/6 t⁴ + 25 t²

C. y = -1/6t⁴ + 25t² + 6t + 10

D. y = 1/2(50 - 2t²)t² + 6t + 10

C

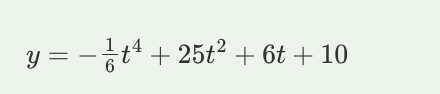
A

B

C

D

D

D

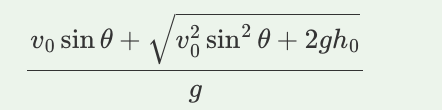
A.

B.

C.

D.

A

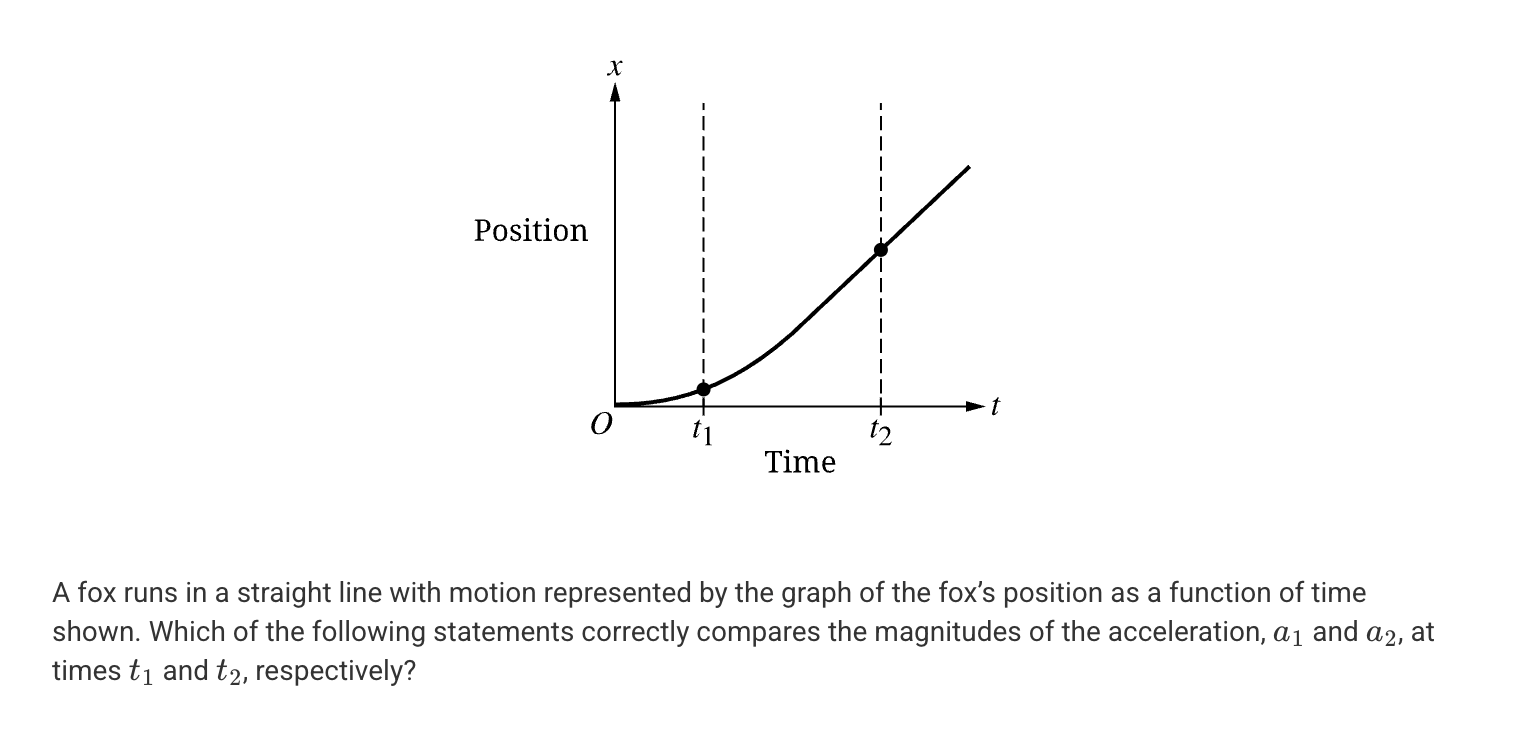
A. a₁ < a₂

B. 0 < a₁ = a₂

C. a₁ > a₂ = 0

D. a₁ > a₂ > 0

C

A. D/2

B. D

C. 2D

D. 4D

C

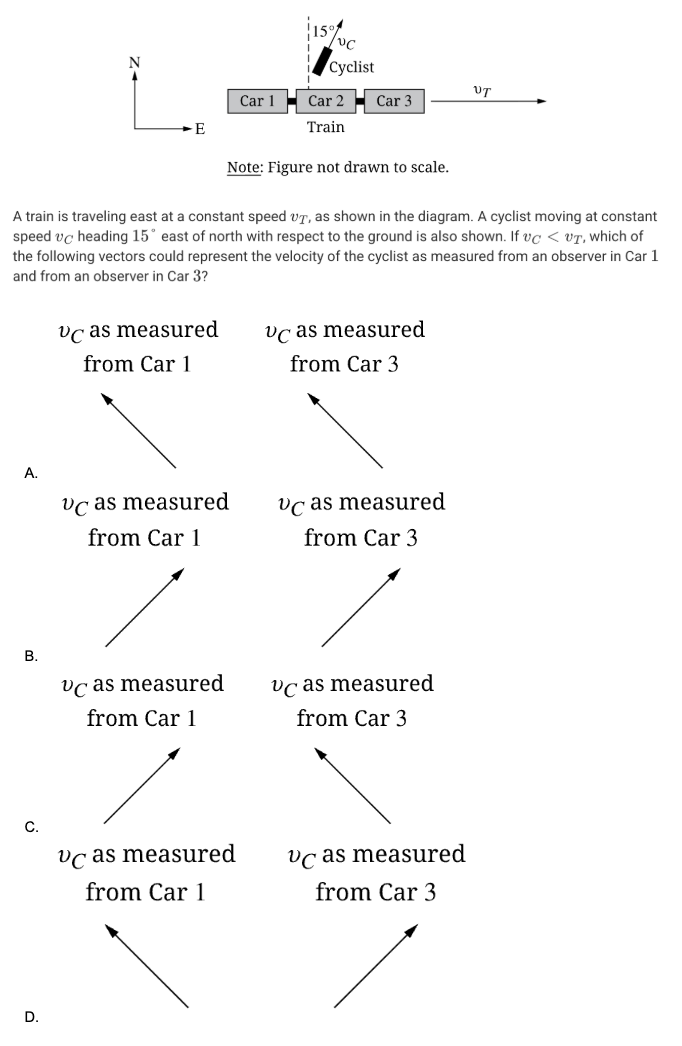
A.

B.

C.

D.

A

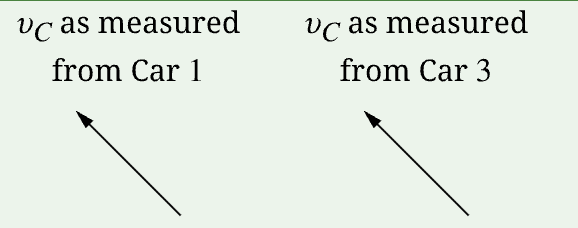
A. a₀ = a₁

B. a₀ > a₁ = 0

C. 0 = a₀ < a₁

D. 0 < a₀ < a₁

D

A. A vector with magnitude zero.

B. A vector with a magnitude greater than zero and less than s.

C. A vector with a magnitude equal to s.

D. A vector with a magnitude greater than s.

D

A.

B.

C.

D.

A

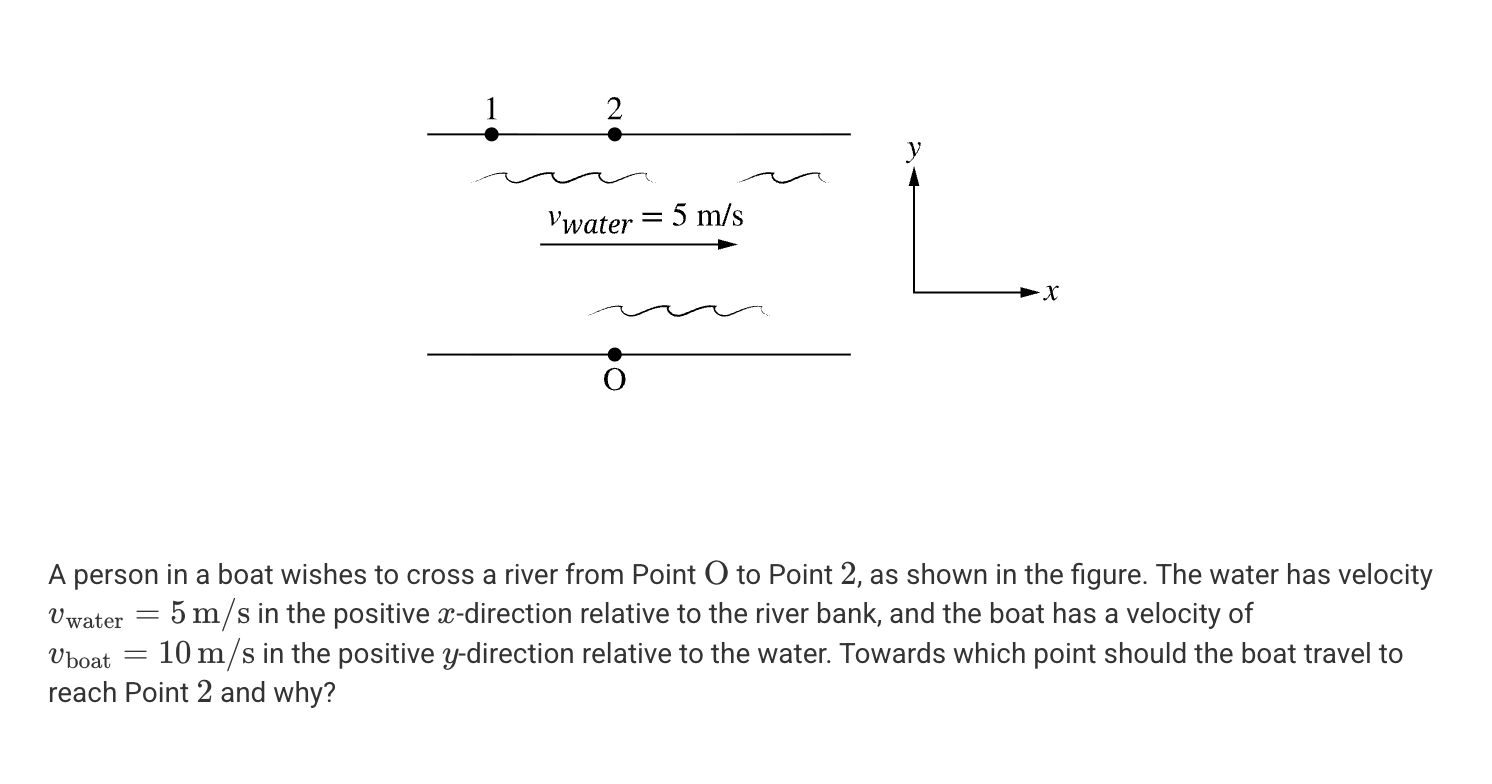
A. Toward Point 1 because the y-component of the boat’s velocity with respect to the water needs to be equal in magnitude to the velocity of the water.

B. Toward Point 1 because the x-component of the boat’s velocity with respect to the water needs to be equal in magnitude to the velocity of the water but in the opposite direction.

C. Toward Point 2 because the magnitude of the boat’s velocity with respect to the water is greater than the magnitude of the velocity of the water.

D. Toward Point y because the y-component of the boat’s velocity with respect to the water is not affected by the motion of the water.

B

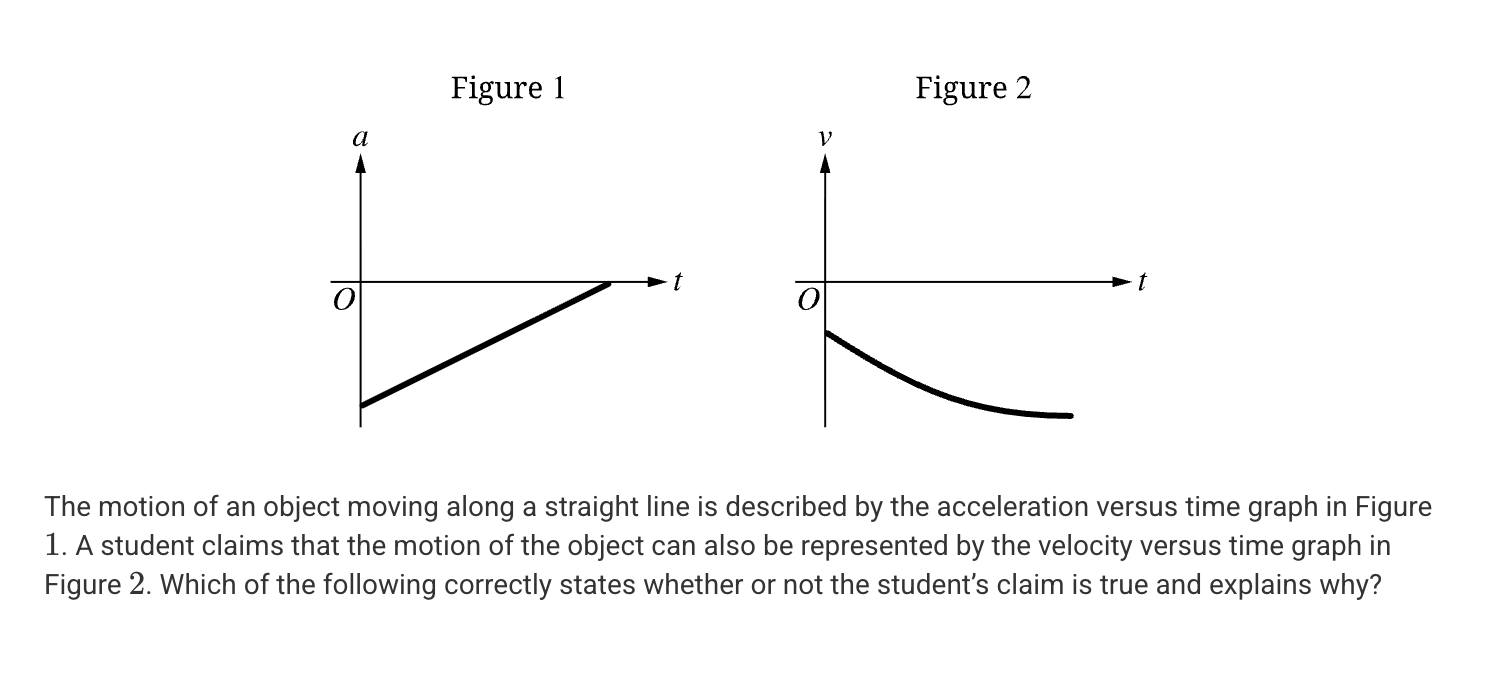
A. No, because the object’s speed is increasing, the acceleration should be positive.

B. No, because the object’s speed is increasing, the acceleration should be increasing in magnitude.

C. Yes, because the area under the curve of the acceleration versus time graph could represent a negative velocity that would be increasing in magnitude.

D. Yes, because the slope of the graph of acceleration versus time is constant, so the velocity of the object approaches a constant value.

C

A. North

B. South

C. East

D. West

A

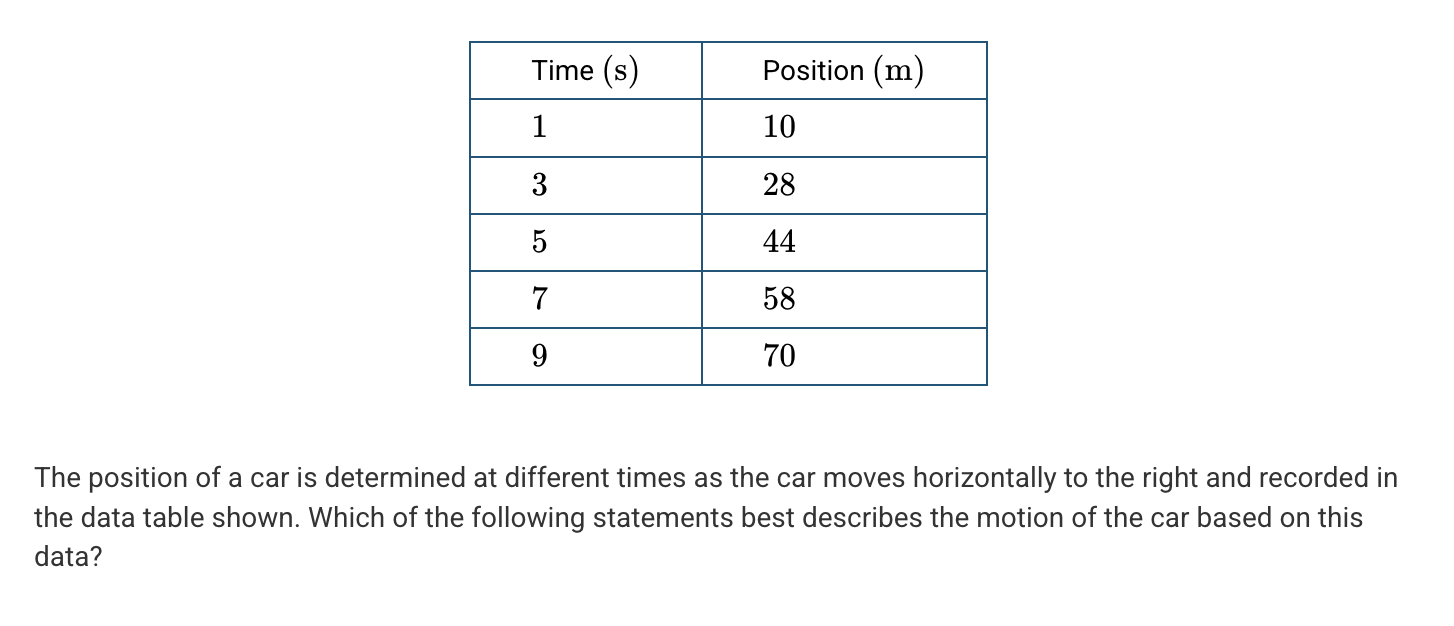
A. The average acceleration of the car is to the left because the ratio of the position to time decreases during the motion of the car.

B. The average acceleration is to the left because the average velocity during successive two second time intervals is decreasing.

C. The average acceleration is to the right because the average velocity of each second time interval is positive.

D. The average acceleration is to the right because the position of the car is increasing.

B

A. h

B. h/2

C. h/4

D. 3h/4

C

A. 20 m/s North

B. 100 m/s at 36.9° North of East

C. 100 m/s at 36.9° North of West

D. 140 m/s East

C

A. v₀ > 10 m/s and θ₀ = 60 degrees

B. v₀ > 10 m/s and θ₀ < 60 degrees

C. v₀ < 10 m/s and θ₀ = 60 degrees

D. v₀ < 10 m/s and θ₀ < 60 degrees

B

A. 53° north of west

B. 53° north of east

C. 53° south of east

D. West

A

A. t_AB > t₀ > t_BA

B. t_BA > t₀ > t_AB

C. (t_AB = t_BA) > t₀

D. t₀ > (t_AB = t_BA)

A

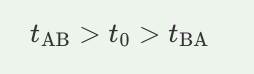
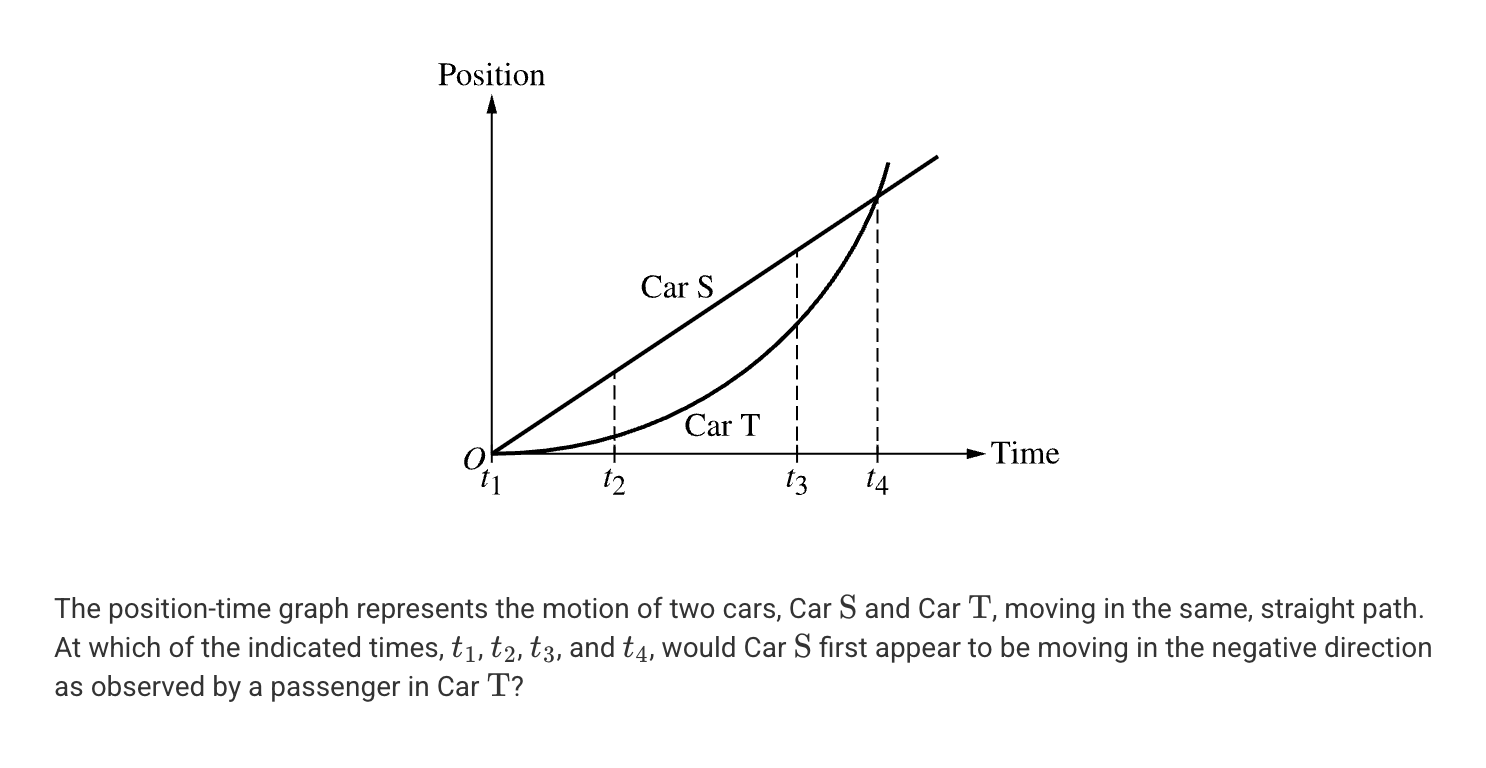
A. t₁

B. t₂

C. t₃

D. t₄

C

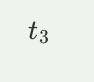
A. 6 m/s²

B. 10 m/s²

C. 11 m/s²

D. 14 m/s²

B

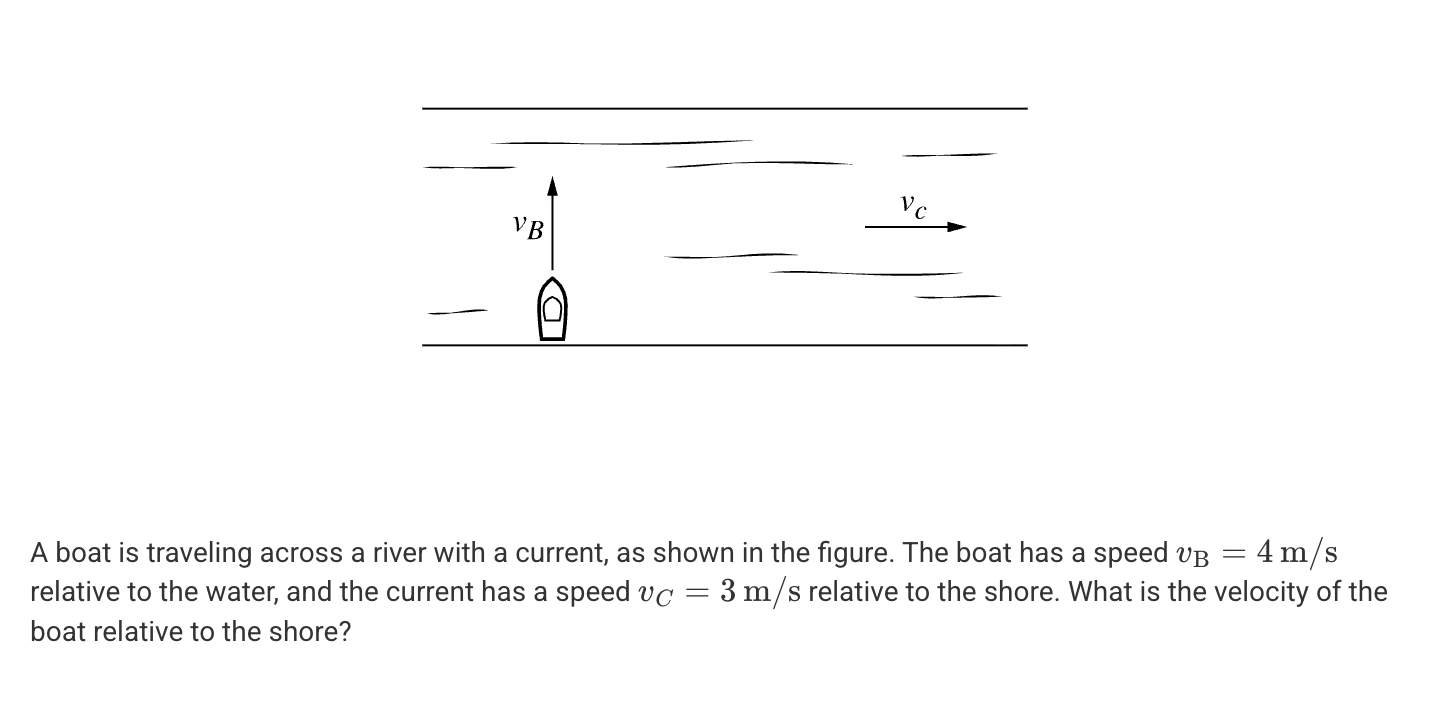
A. 3 m/s

B. 4 m/s

C. 5 m/s

D. 7 m/s

C

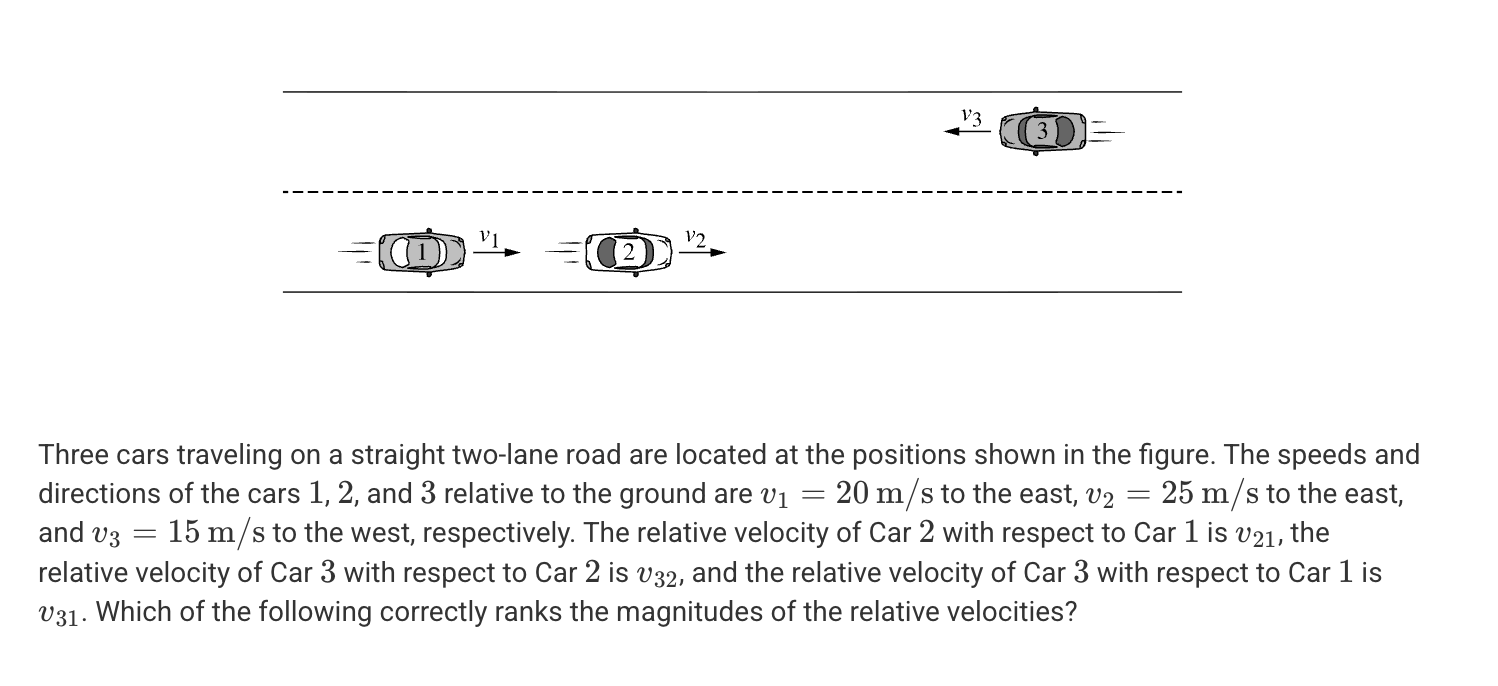
A. |v₃₁| = |v₃₂| = |v₂₁|

B. |v₂₁| > |v₃₂| > |v₃₁|

C. |v₃₂| > |v₃₁| = |v₂₁|

D. |v₃₂| > |v₃₁| > |v₂₁|

D

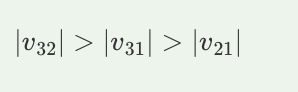
A. 10 m/s

B. 13 m/s

C. 26 m/s

D. 28 m/s

C

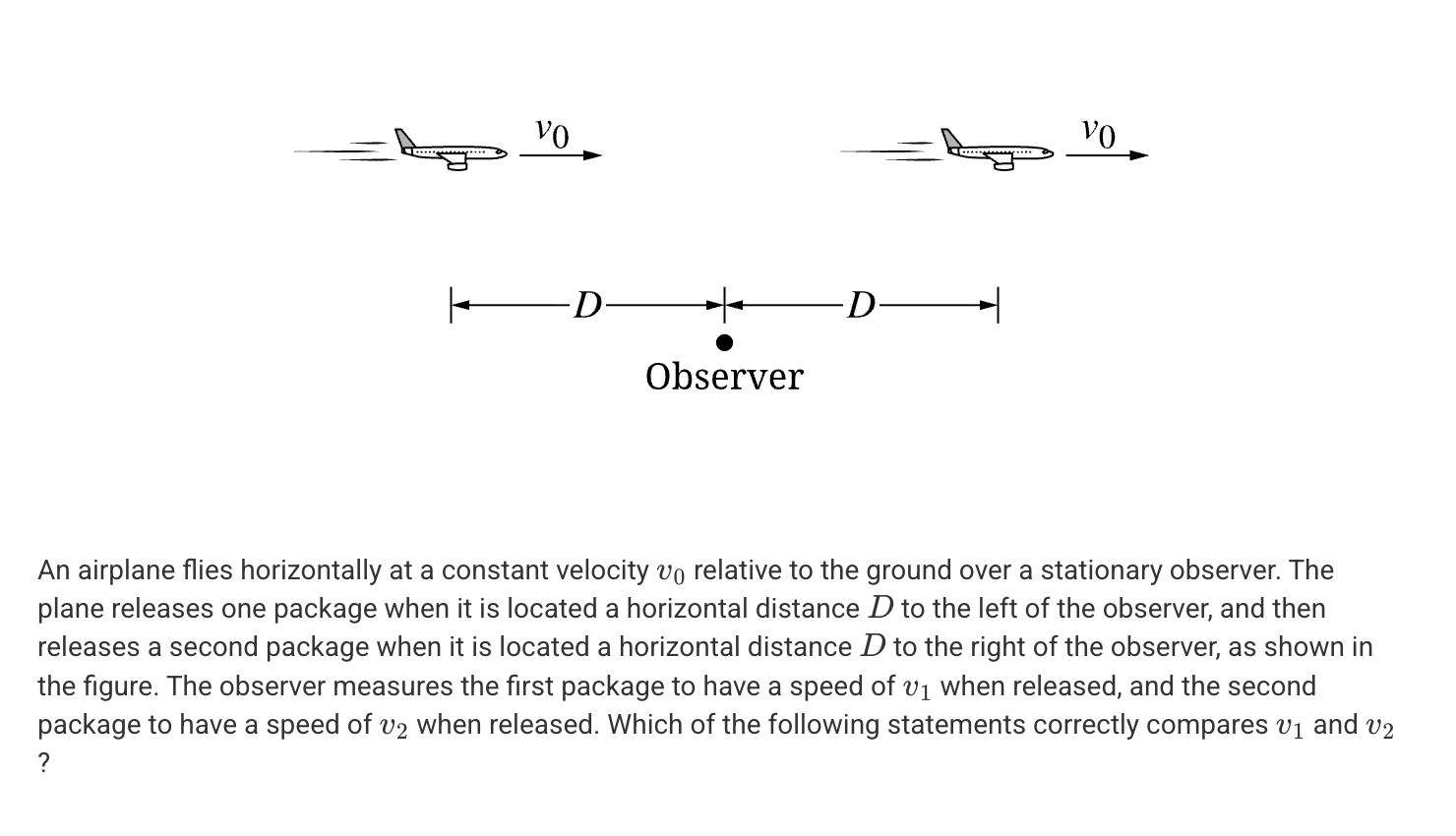
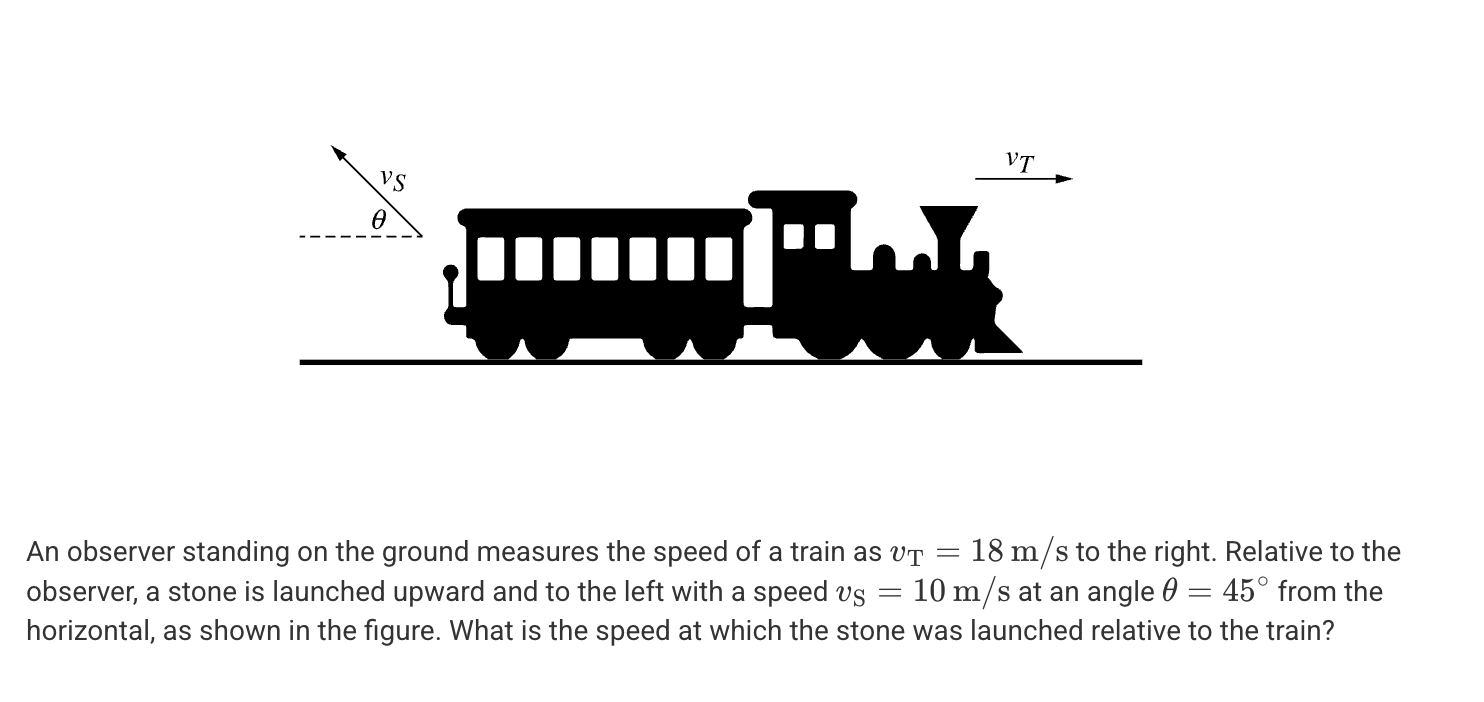
A. v₁ = v₂ = 0

B. v₁ = v₂ > 0

C. v₁ < v₂

D. v₁ > v₂

B

A. 1 m/s²

B. 4 m/s²

C. 5 m/s²

D. 7 m/s²

C

A.

B.

C.

D.

D

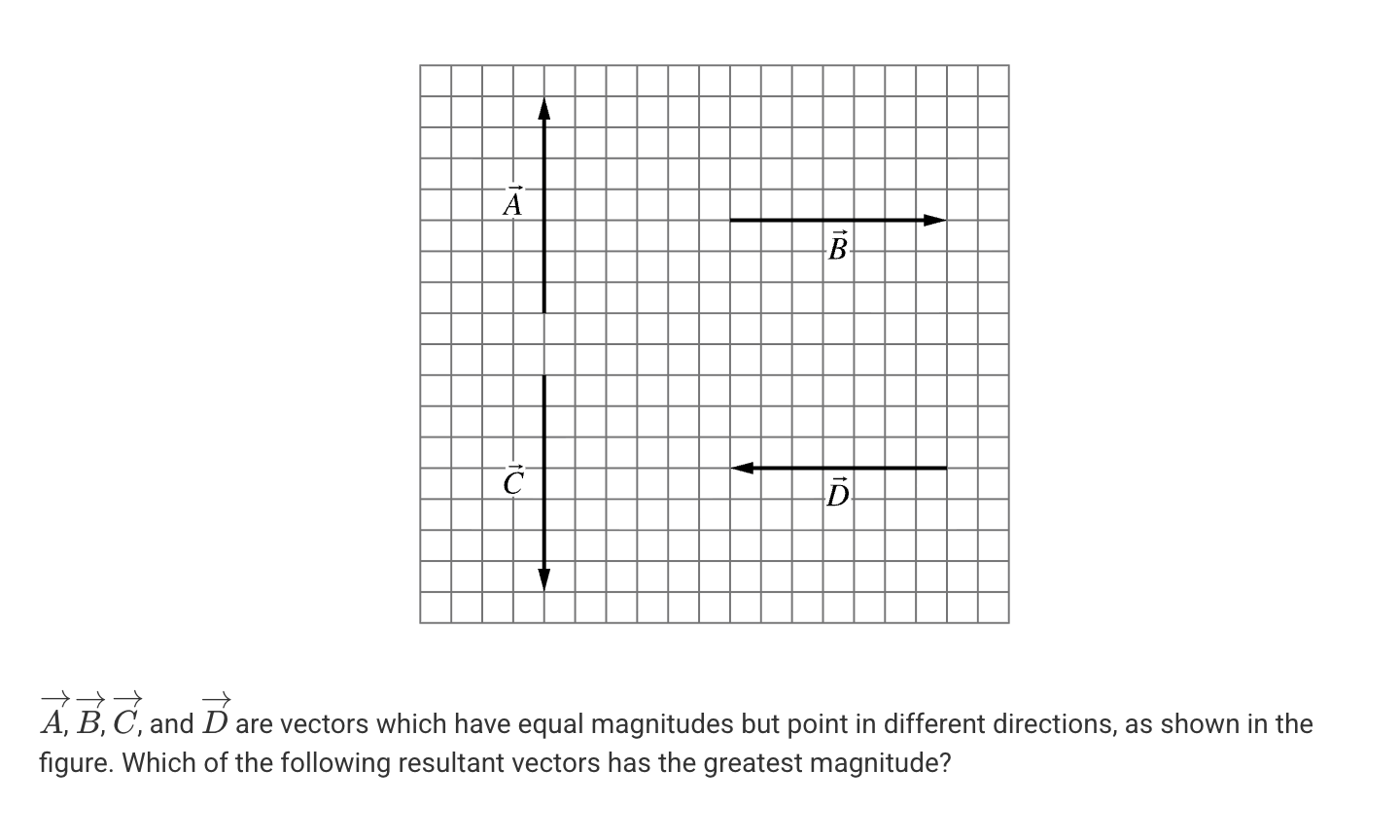
A. A + B

B. C - D

C. B + D

D. C - A

D

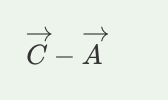
A. It is a vector that has a smaller magnitude than both A and B, but nonzero.

B. It is a vector that has a greater magnitude than both A and B.

C. It is a vector of length zero.

D. It is a vector that has the same magnitude as both A and B.

A

A.

B.

C.

D.

A

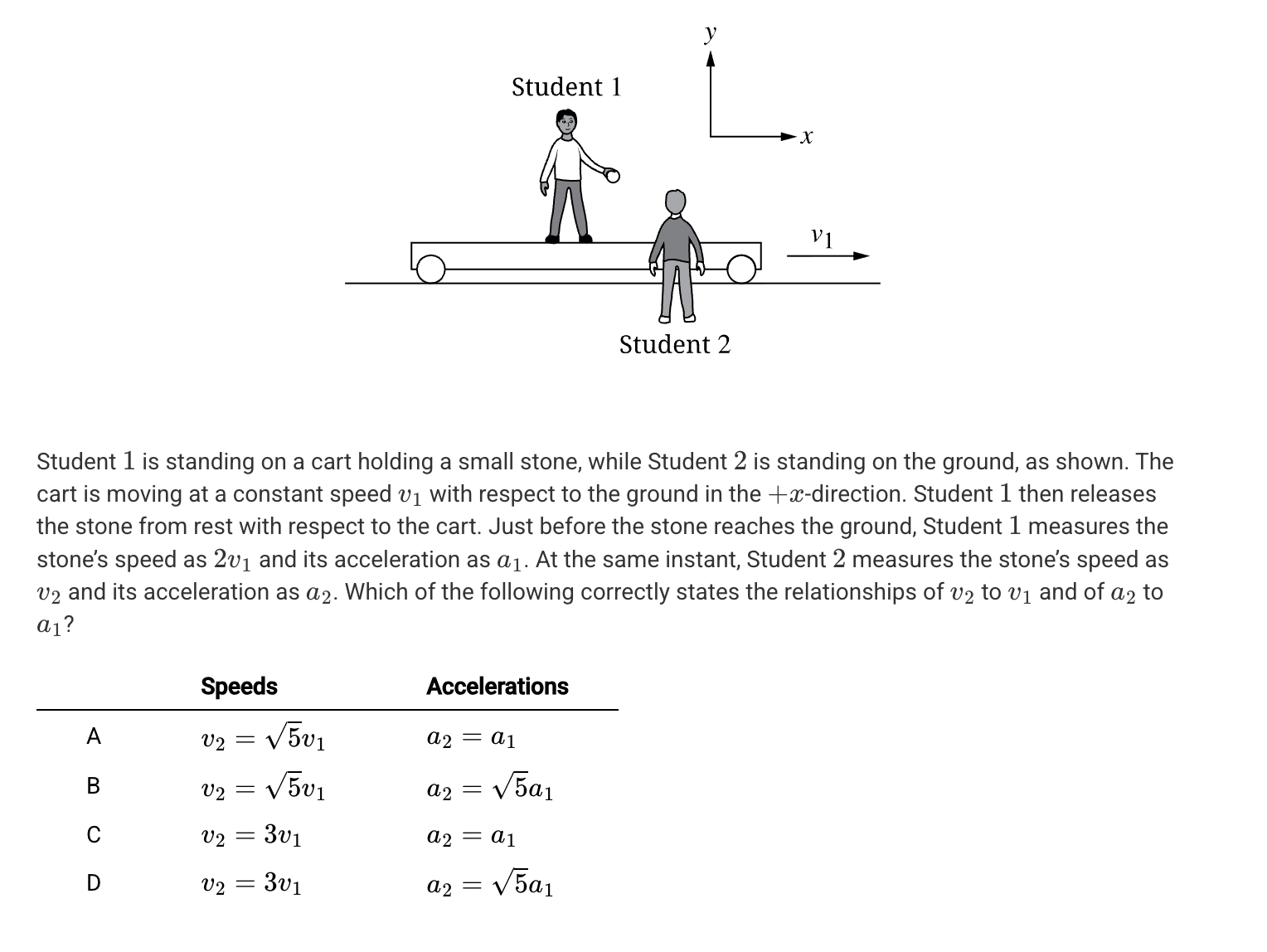
A. 11.0 m/s

B. 12.0 m/s

C. 15.6 m/s

D. 19.6 m/s

C

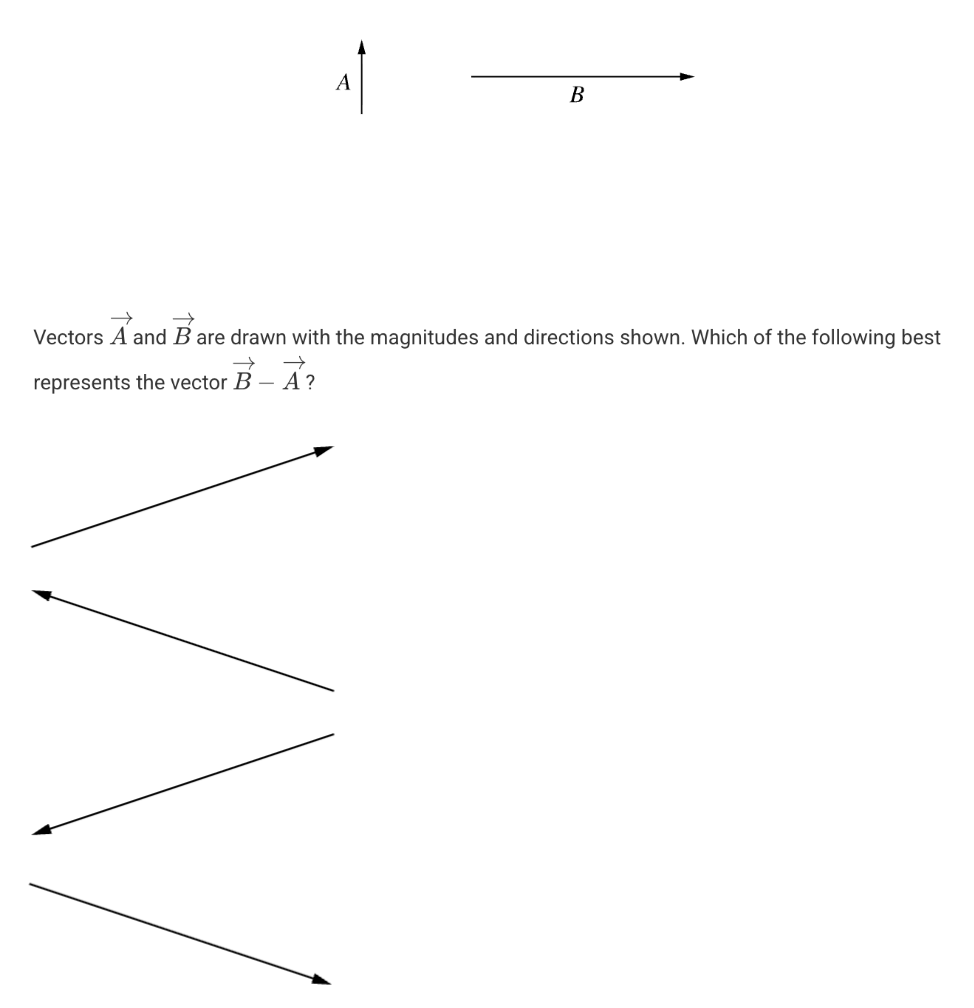
A.

B.

C.

D.

D

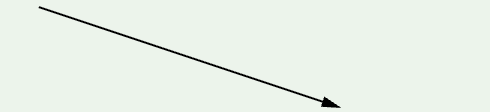
A. A(sinθ-cosθ)

B. A(cosθ-sinθ)

C. A(cosθ+sinθ)

D. A/tanθ

A

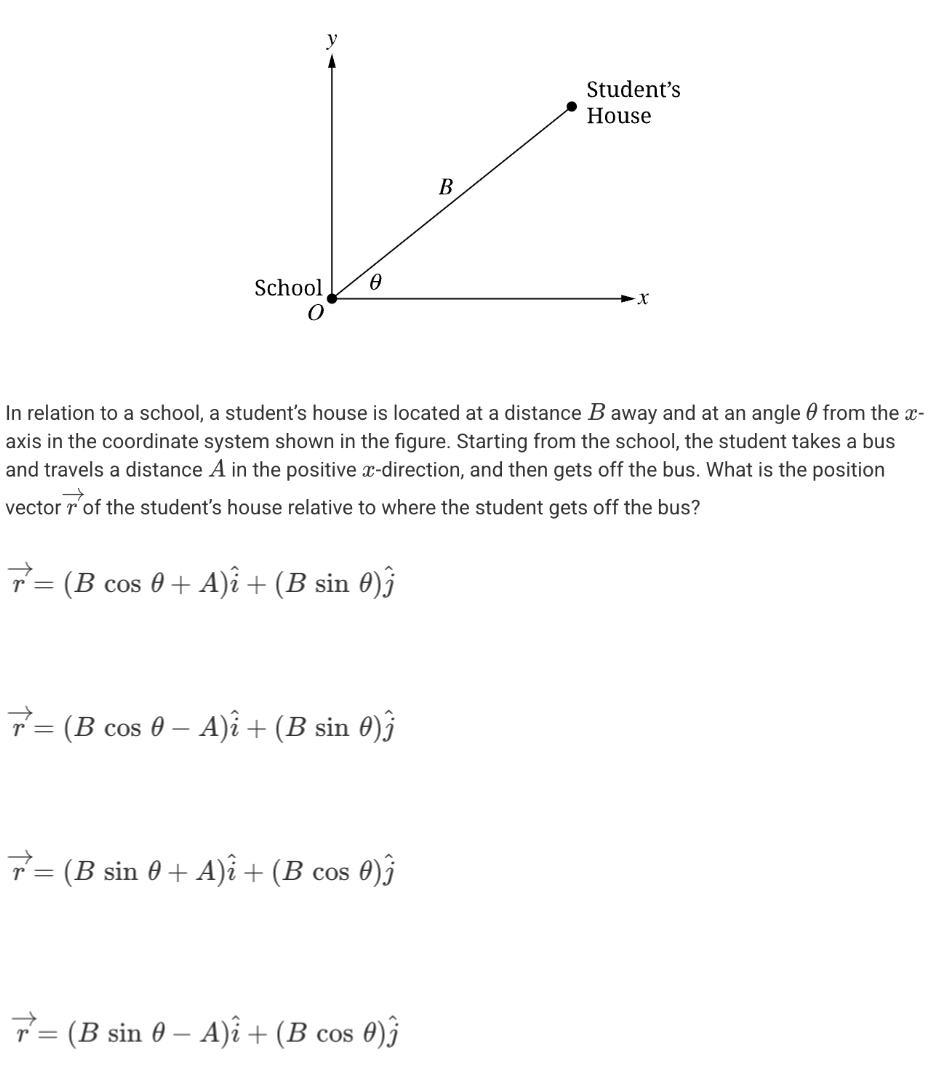
A.

B.

C.

D.

B

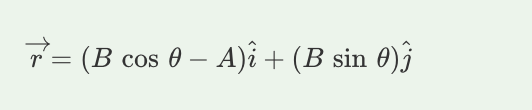
A.

B.

C.

D.

B

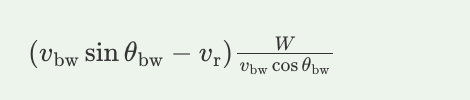
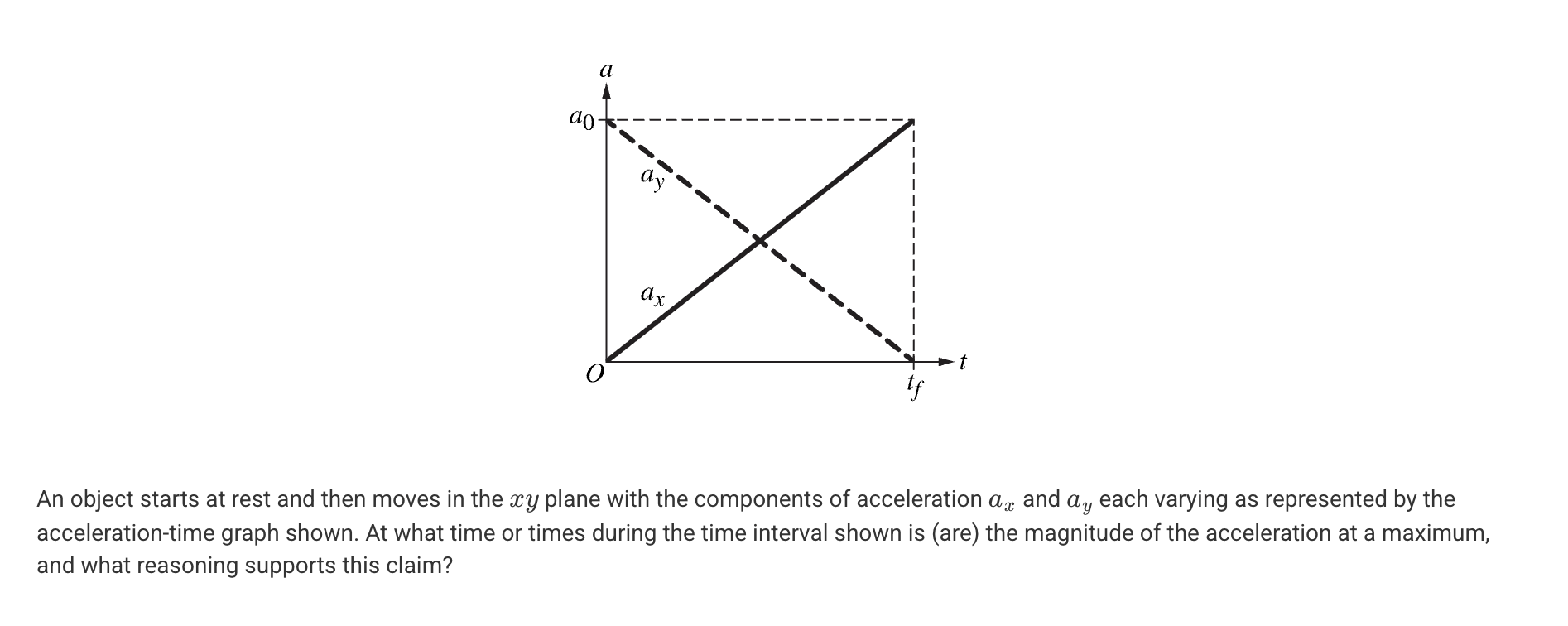
A. At t = t_f/2. The product a_xa_y is at its greatest value

B. At t = t_f/2. a_x and a_y are equal in magnitude.

C. At t = 0 and t = t_f • |a_x - a_y| is at its greatest value.

D. At t = 0 and t = t_f • a_x² + a_y² is at its greatest value.

D

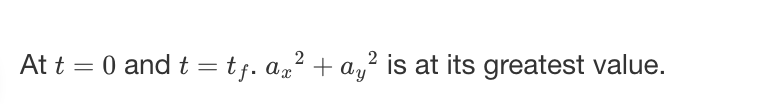
A. y₂ = y₁

B. y₂ = sqrt2 y₁

C. y₂ = 2y₁

D. y₂ = 4y₁

D

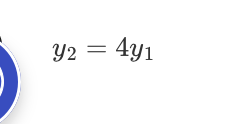
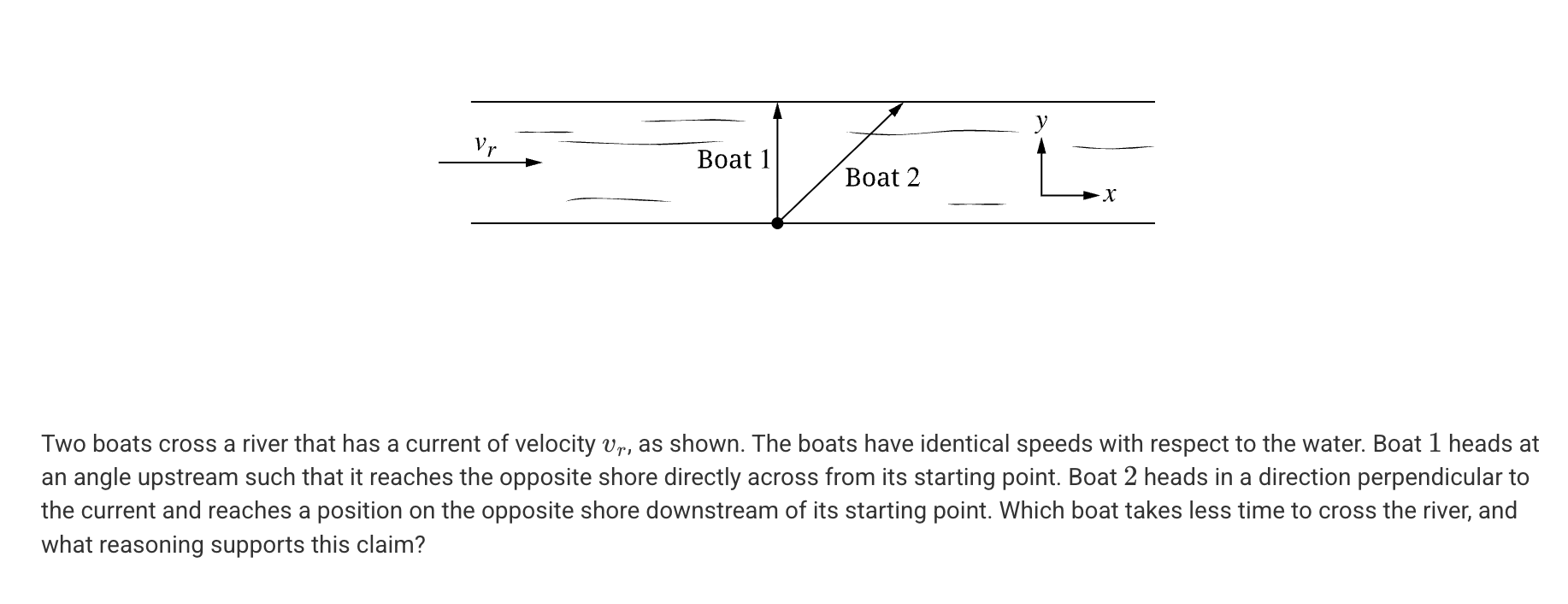
A. Boat 1 takes less time because it travels a shorter distance than Boat 2.

B. Boat 1 takes less time because its velocity with respect to the water and the current velocity add together, giving Boat 1 a greater resultant velocity.

C. Boat 2 takes less time because its velocity has a greater y-component with respect to the ground than Boat 1.

D. Boat 2 takes less time because the current increases the boat’s speed relative to the ground.

C

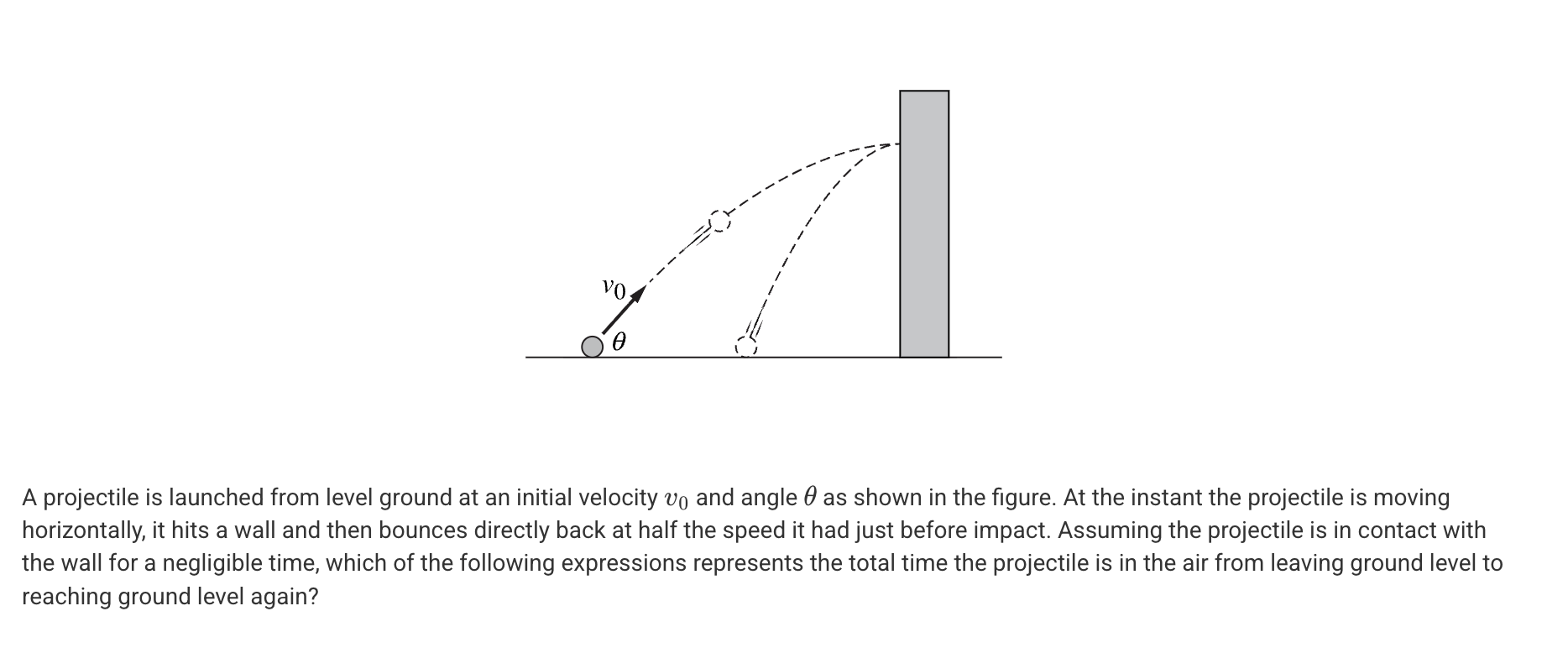
A. v₀sinθ/g

B. 3/2 v₀sinθ/g

C. 2 v₀sinθ/g

D. 4 v₀sinθ/g

C

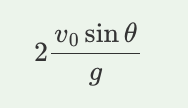
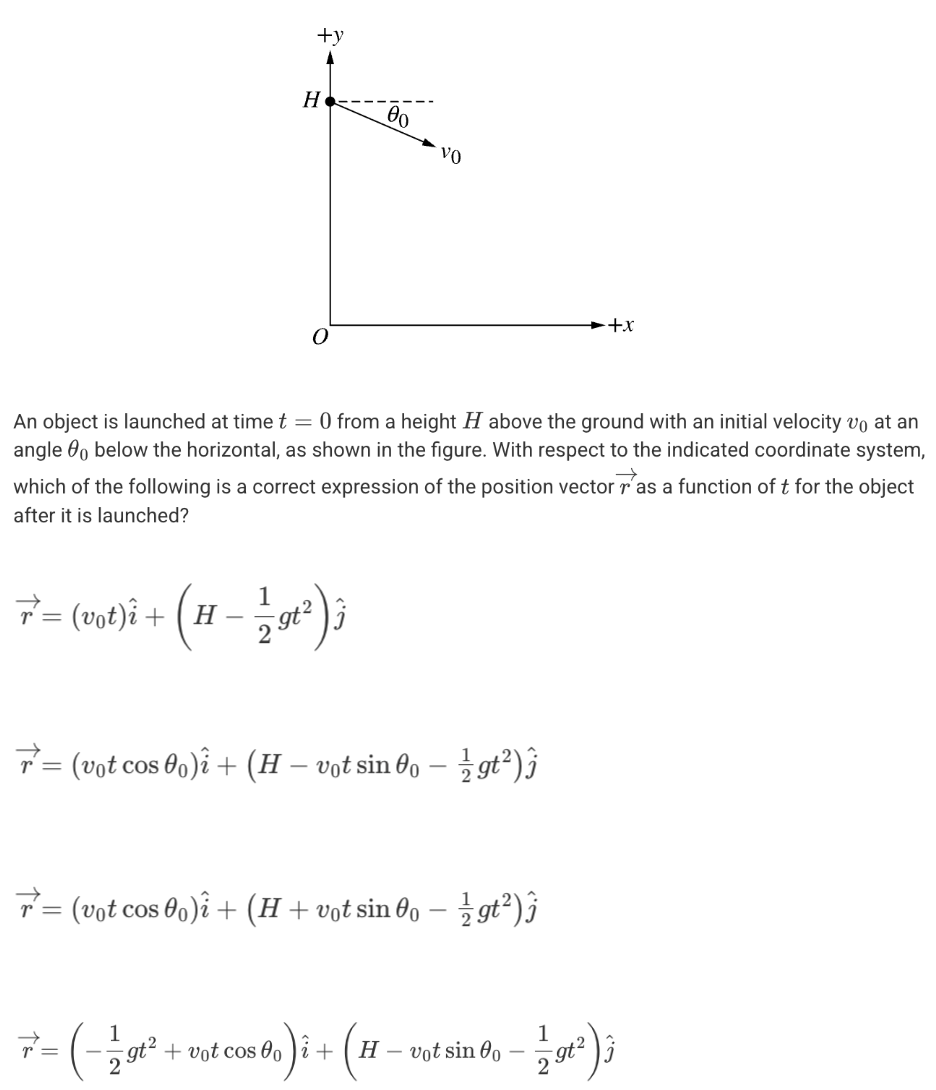
A.

B.

C.

D.

B

A. v

B. 2v

C. 4vsinθ

D. 4v

B

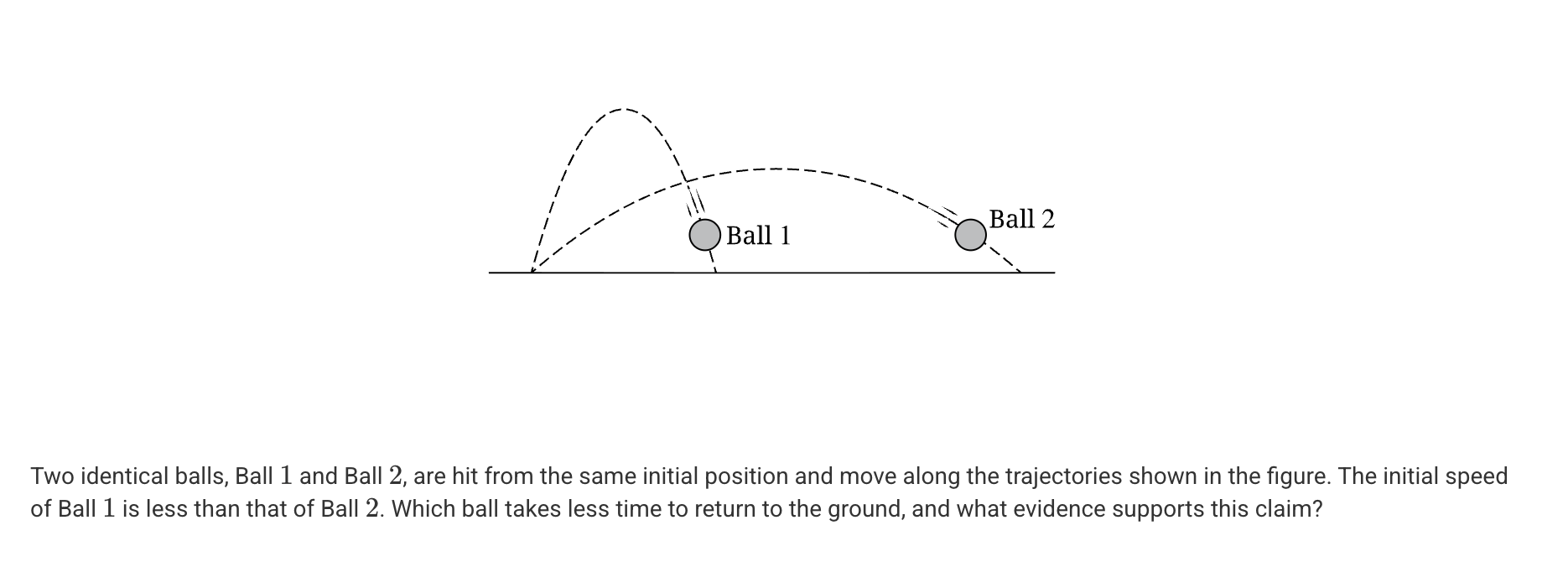
A. Ball 1 takes less time. Its initial speed is less than that of Ball 2.

B. Ball 1 takes less time. The horizontal distance it travels is less than that of Ball 2.

C. Ball 2 takes less time. Its initial speed is greater than that of Ball 1.

D. Ball 2 takes less time. The maximum height it reaches is less than that of Ball 1.

D

A.

B.

C.

D.

A

A. 4H

B. 2H

C. H

D. H/2

E. H/4

E

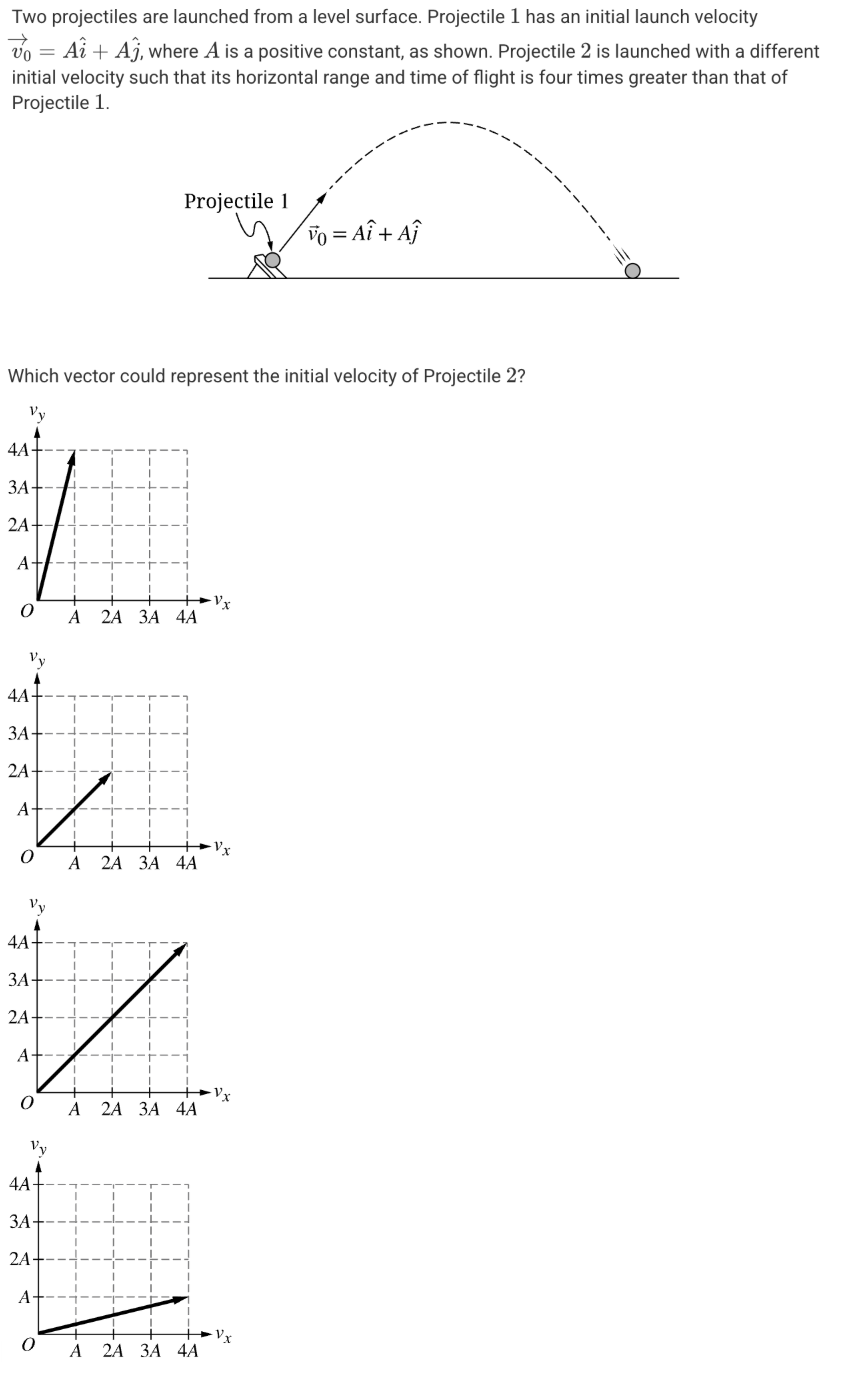
A.

B.

C.

D.

A

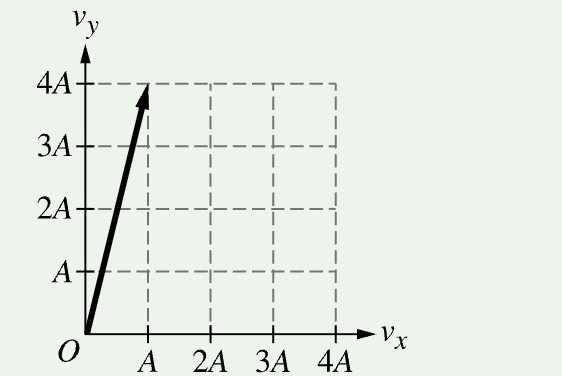
A.

B.

C.

D.

E.

C

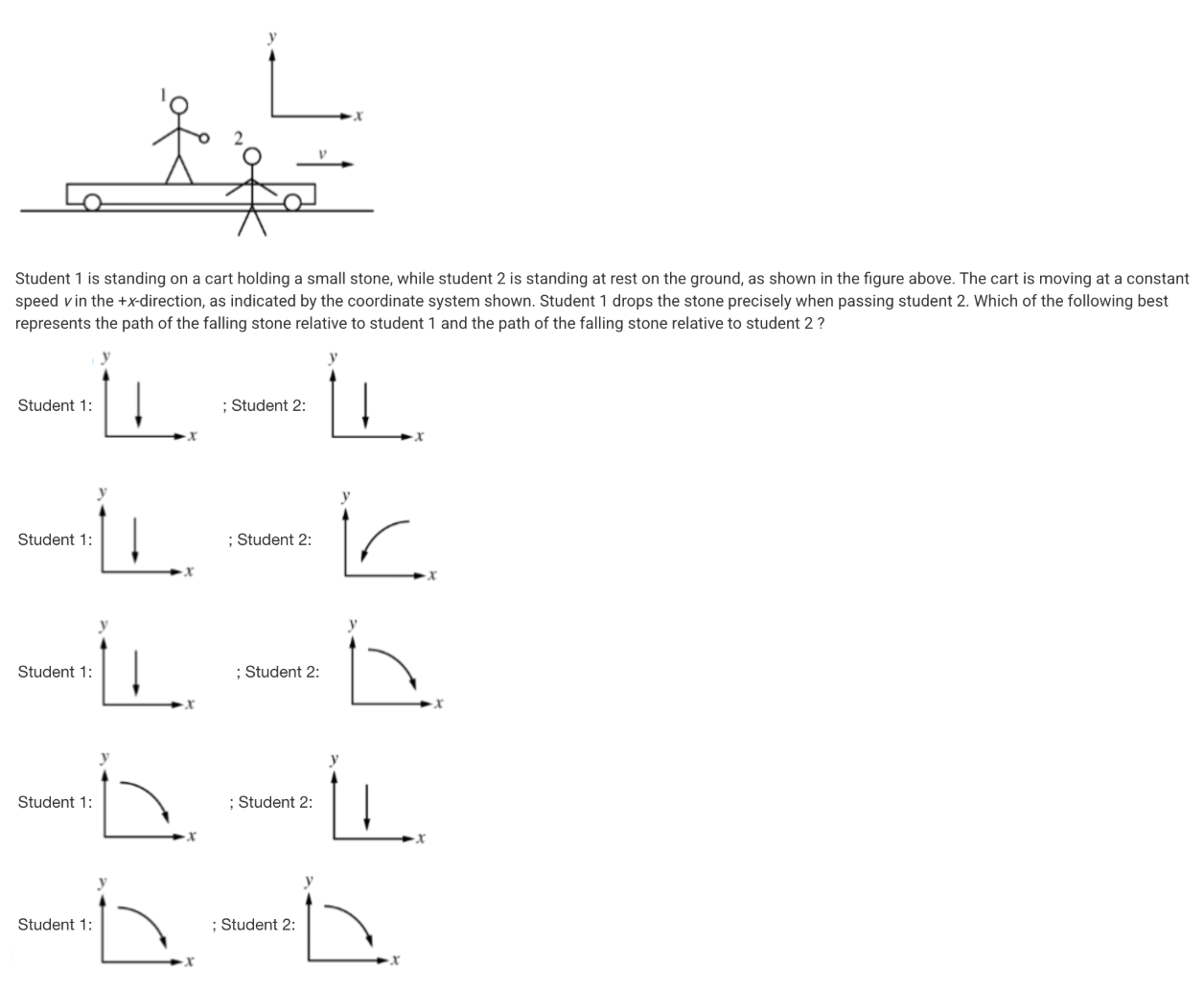
A. 15m

B. 30m

C. 45m

D. 60m

E. 75m

A

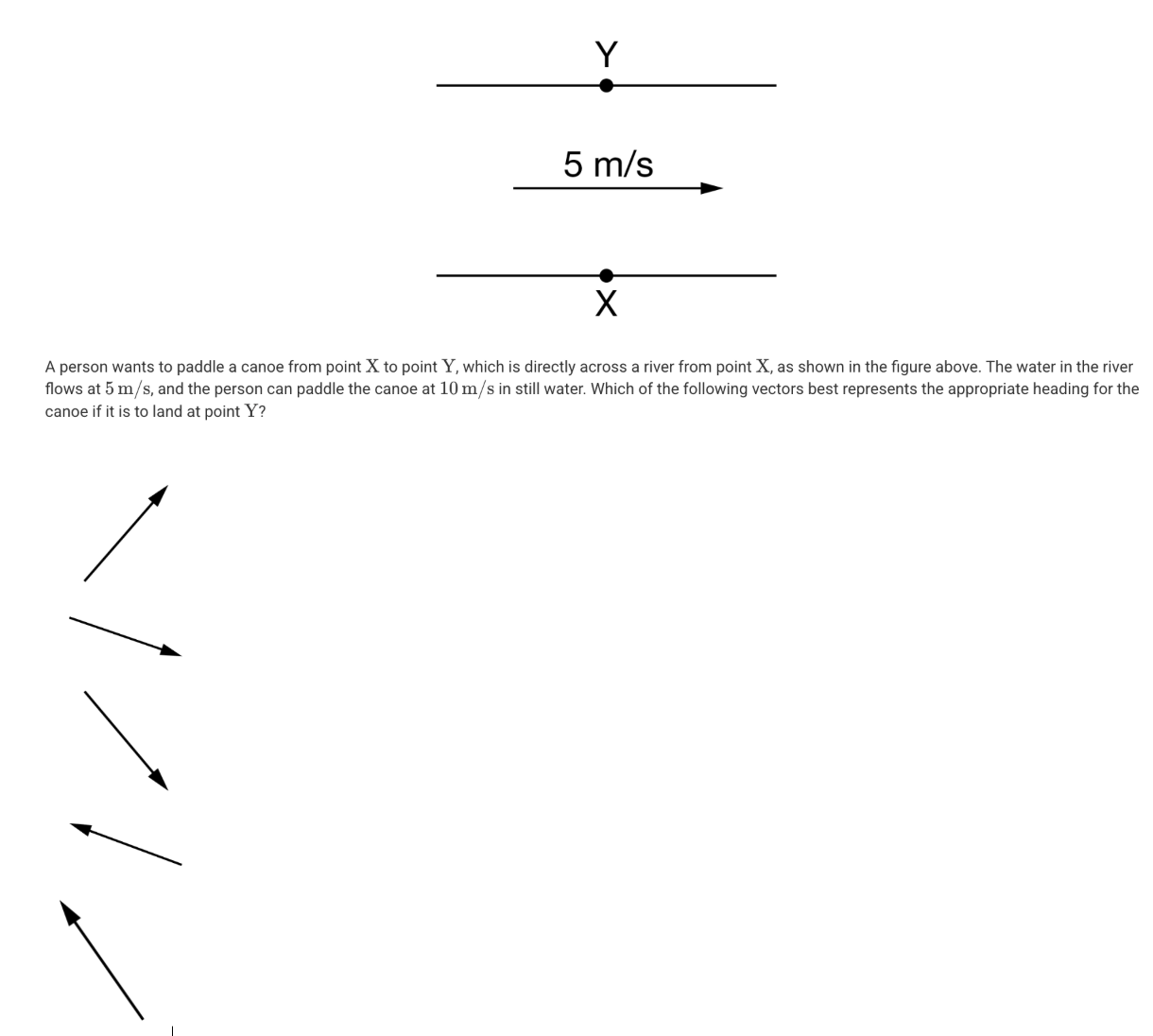
A.

B.

C.

D.

E.

E

A. 0

B. 16 m/s

C. 19 m/s

D. 25 m/s

C

A.

B.

C.

D.

E.

A

A.

B.

C.

D.

C

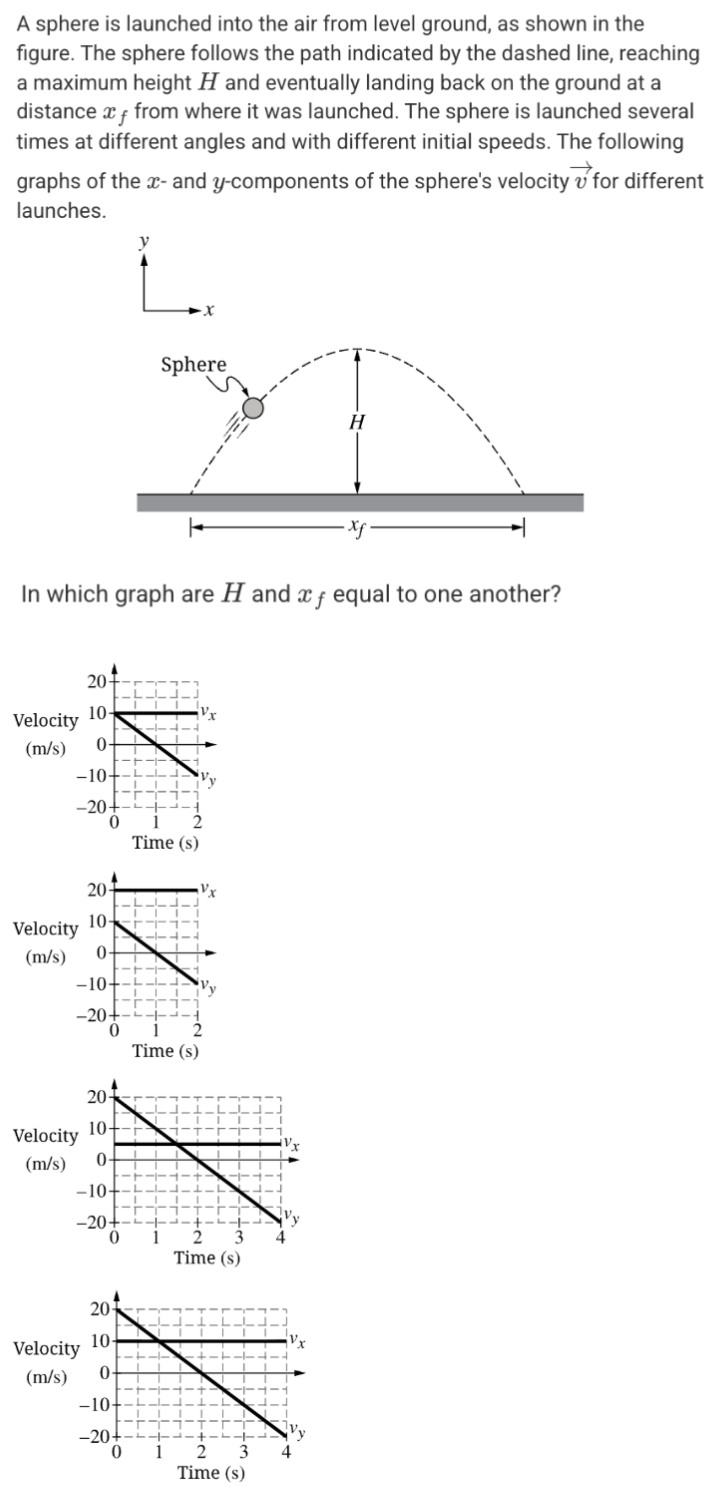
A.

B.

C.

D.

E.

B

A.

B.

C.

D.

E.

D

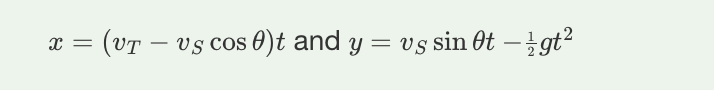
A block is at rest on a desk’s horizontal surface. A student correctly identifies the forces exerted on the block as the force of Earth on the block and the force of the desk on the block. A book then is placed between the block and the desk. Which objects exert forces of equal magnitude on the block after the book has been introduced?

A. Earth and the book

B. Earth and the desk

C. The book and the desk

D. Earth, the book, and the desk

A

A student pushes a box across a rough horizontal surface. Which of the following includes all the forces exerted on the box that are a result of interatomic electric forces?

A. The force of friction only

B. The force of friction and the normal force

C. The force of friction, the normal force, and the force exerted by the student

D. The force of friction, the normal force, the force exerted by the student, and the weight of the box.

C

A.

B.

C.

D.

C

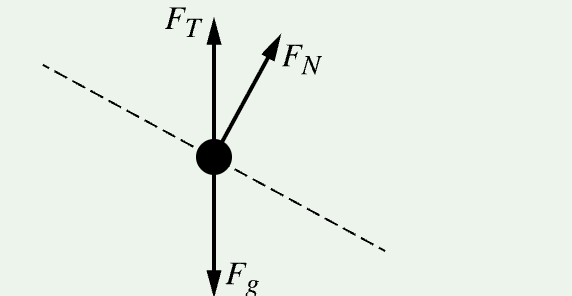
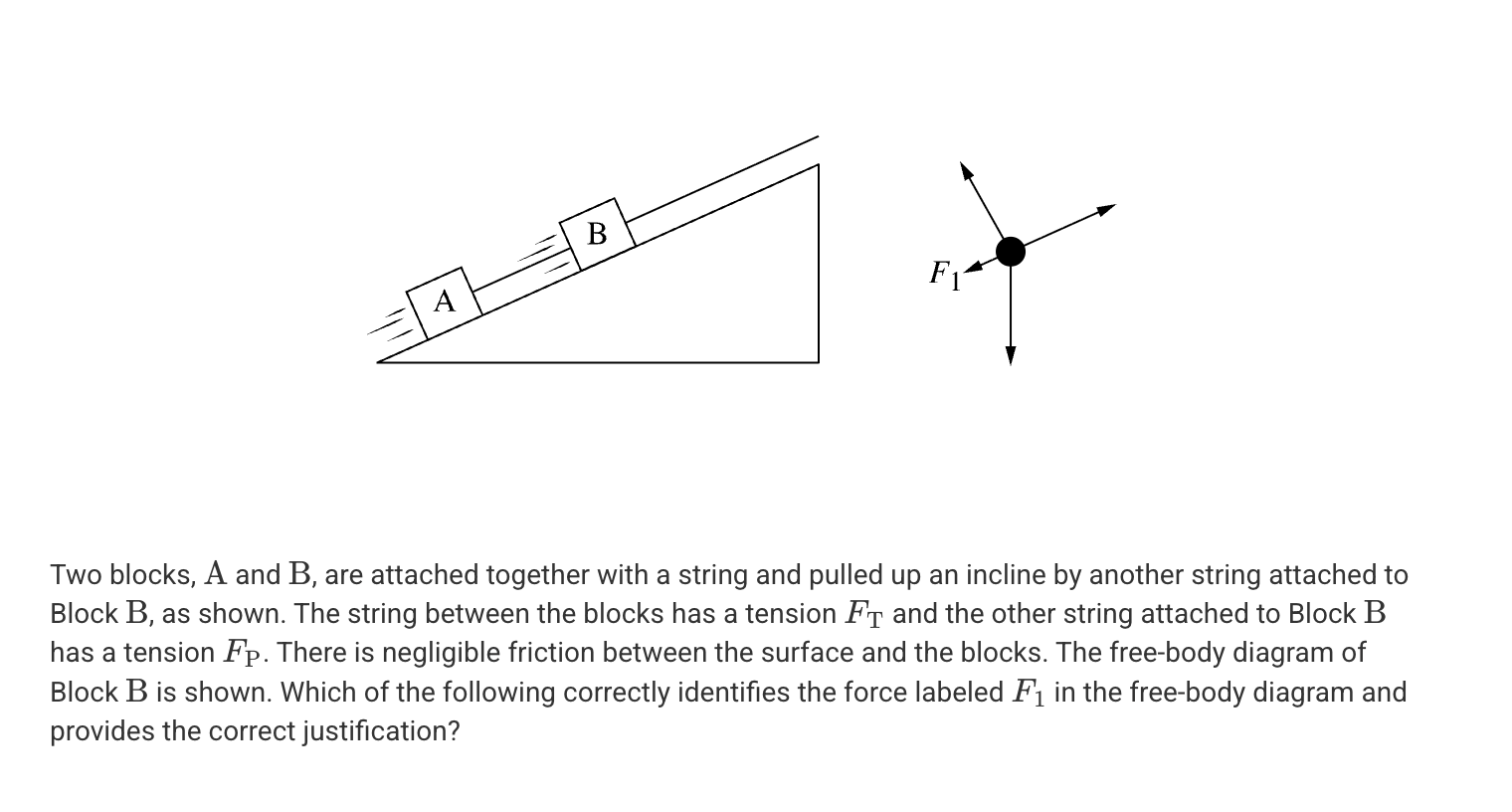
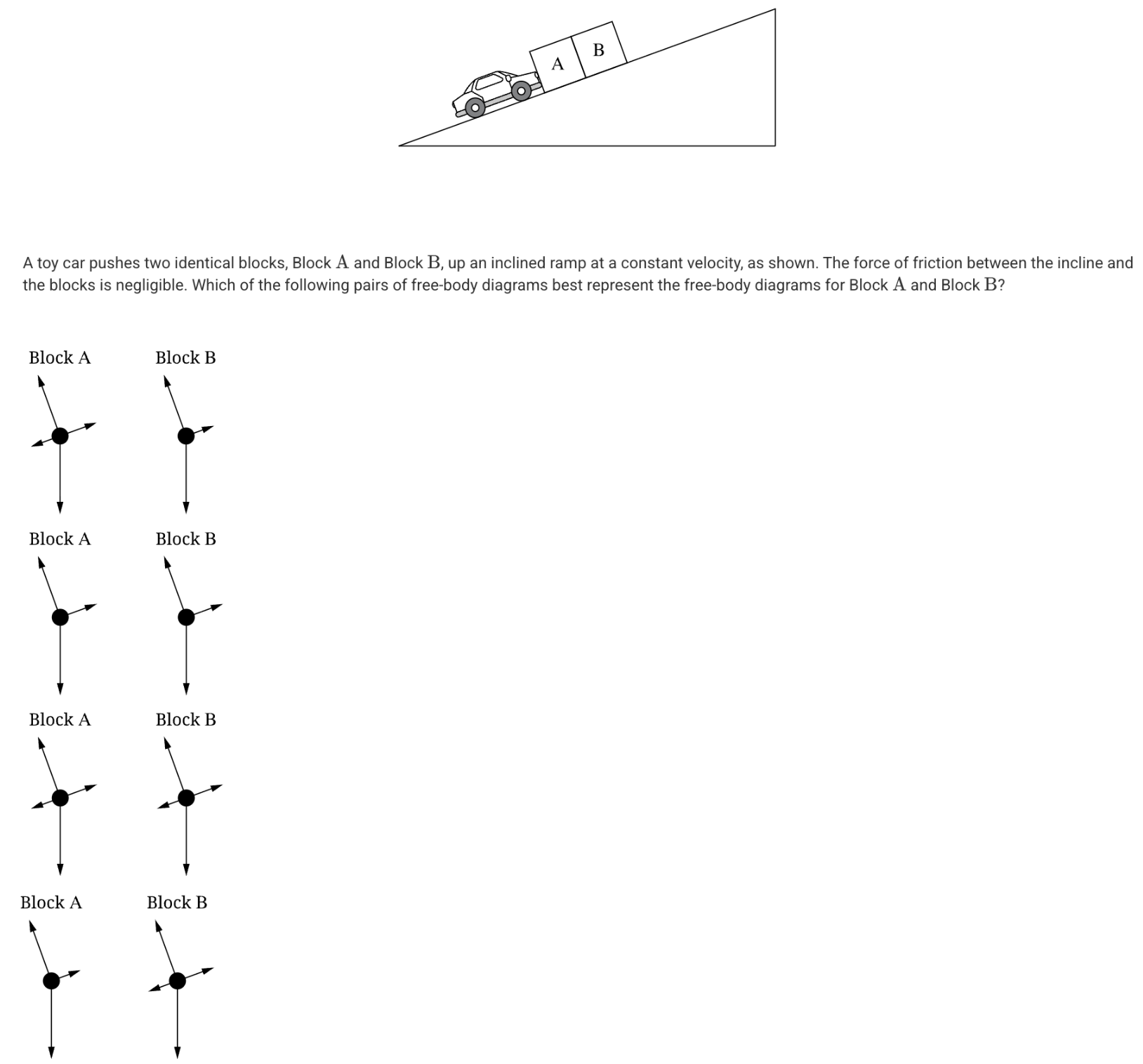
A. F₁ = F_P because Block B is pulling the string down the incline.

B. F₁ = F_P because the string attached only to Block B is also pulling Block A up the incline

C. F₁ = F_T because Block A is being pulled up the incline by the string which is attached to it

D. F₁ = F_T because the string between the blocks is pulling Block B down the incline.

D

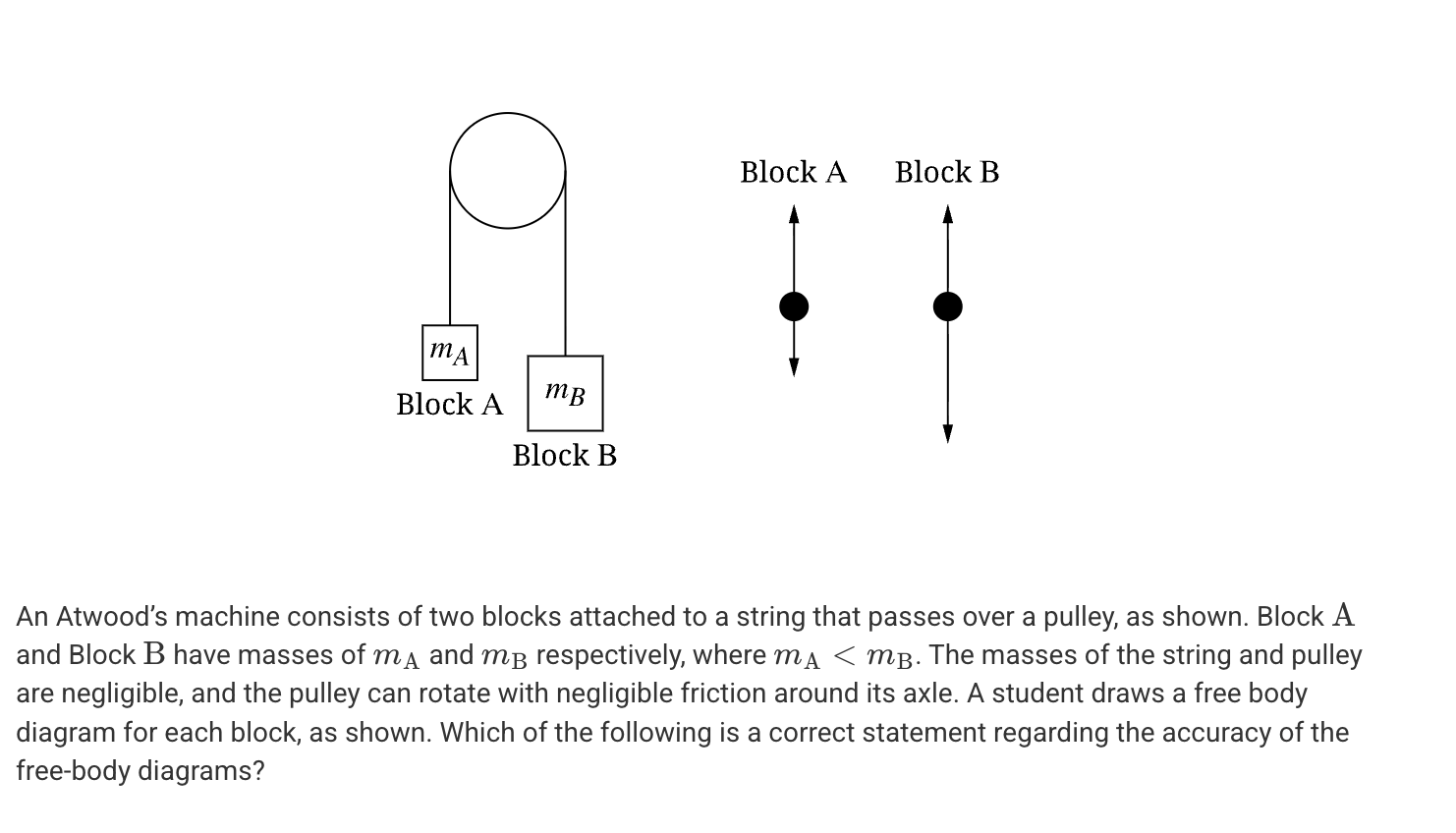
A. The diagrams are accurate because the force of the string is less than the force of gravity on both blocks.

B. The diagrams are accurate because the string is pulling up with the same force on both blocks and the gravitational force is greater for Block .

C. The diagrams are not accurate because the string will pull up with more force on Block than Block since Block has a smaller mass.

D. The diagrams are not accurate because the gravitational force is independent of mass and will be the same on both blocks.

B

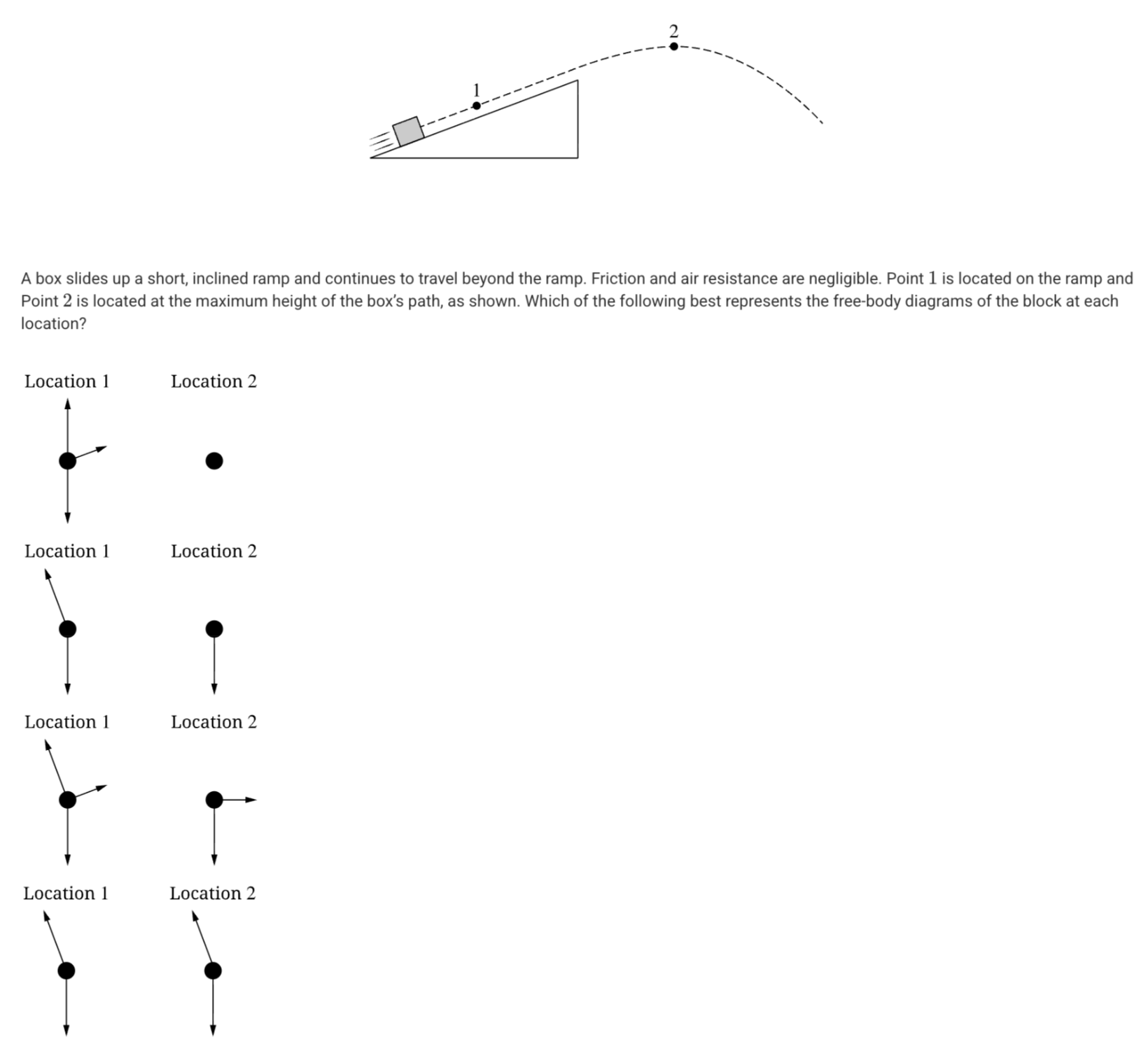
A.

B.

C.

D.

B

A.

B.

C.

D.

A

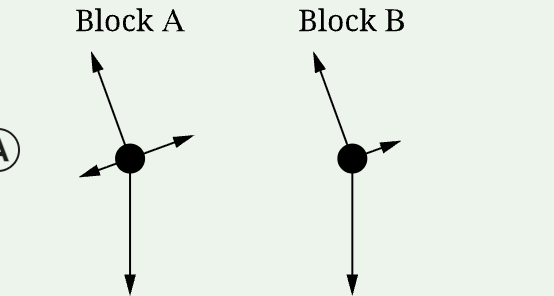
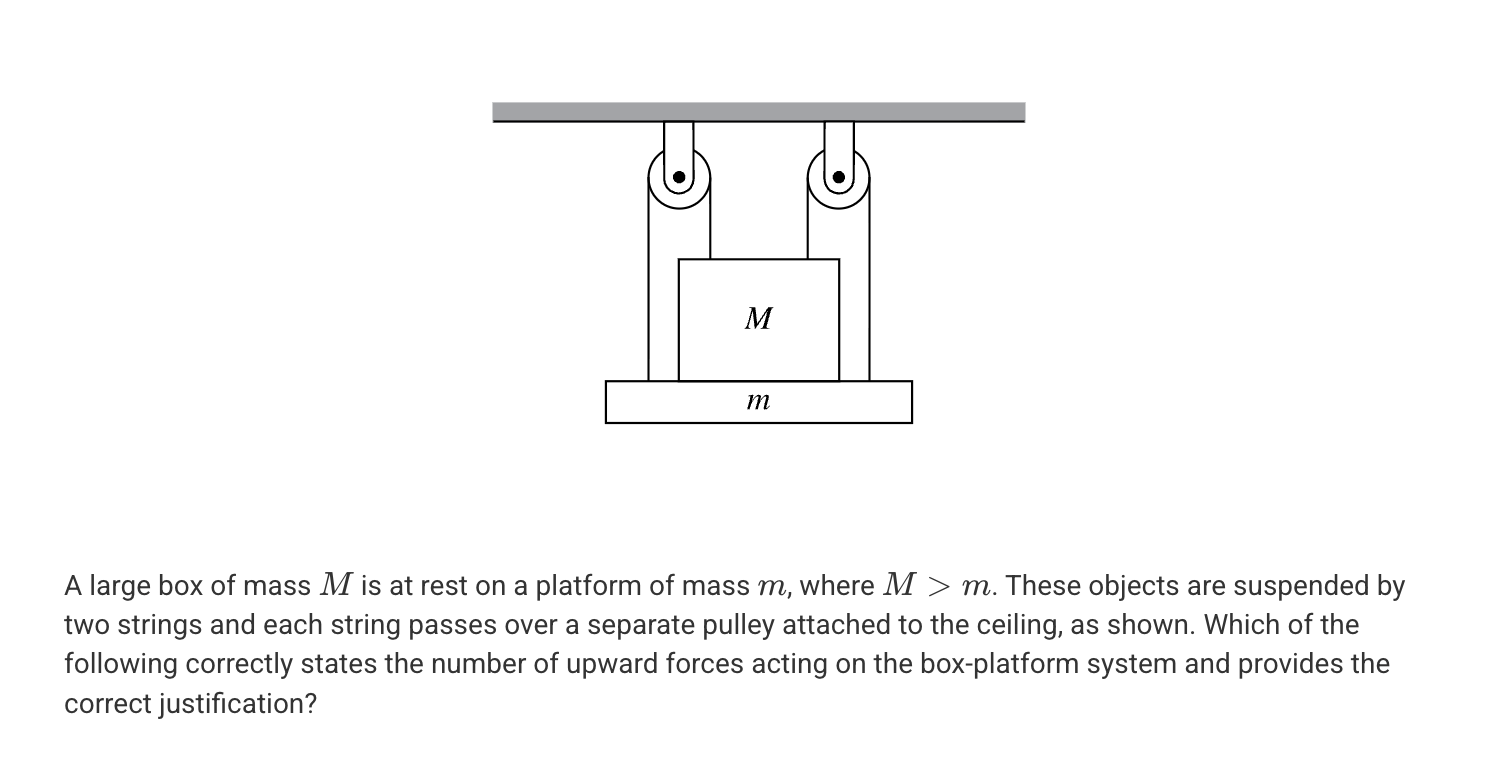
A. Two upward forces are exerted on the system because there are two strings which exert upward forces on the system.

B. Two upward forces are exerted on the system because there are two pulleys which exert upward forces on the system.

C. Four upward forces are exerted on the system because there are two strings and two pulleys which exert upward forces on the system.

D. Four upward forces are exerted on the system because there are four tensions which exert upward forces on the system.

D

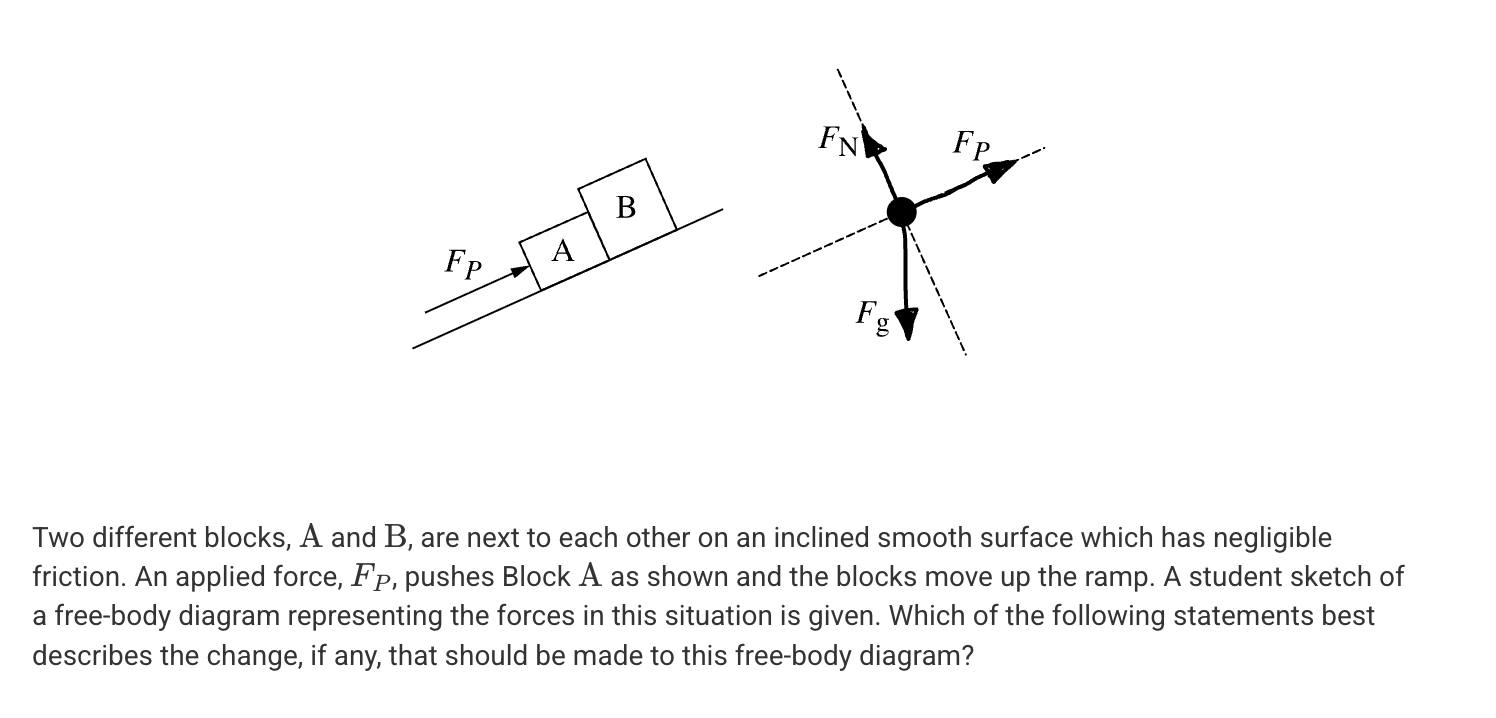
A. No change is needed.

B. The F_P arrow should be labeled as F_AB for the force that Block A exerts on Block B.

C. There should be an additional force F_BA pointing down the incline.

D. Each of the above statements is possible depending on which object or system the free-body diagram represents.

D

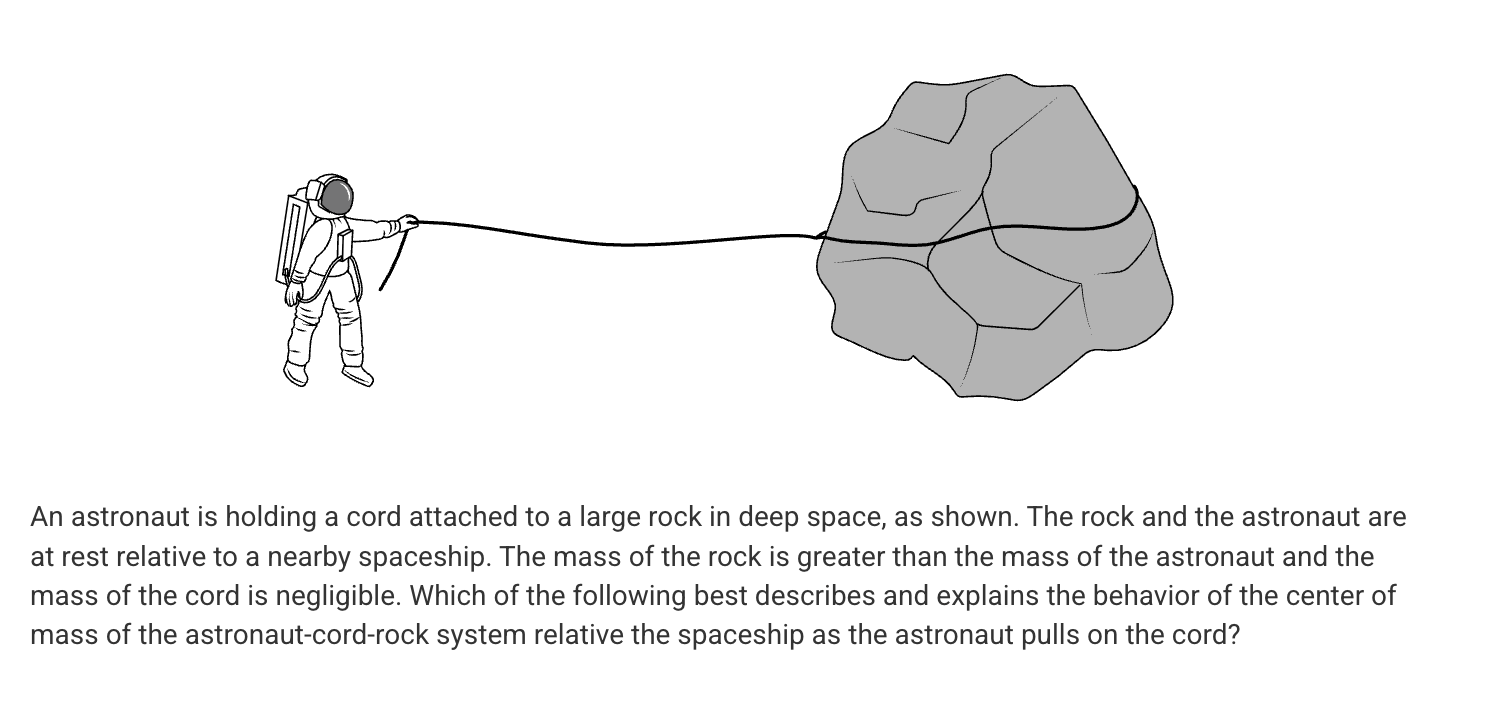
A. The center of mass shifts to the right because the astronaut moves to the right and the rock remains stationary.

B. The center of mass shifts to the right because the force on the astronaut is greater than the force on the rock due to their different masses.

C. The center of mass does not move because the astronaut and the rock each move the same distance towards the original location of the center of mass.

D. The center of mass does not move because the astronaut will move a larger distance to the right than the rock moves to the left.

D

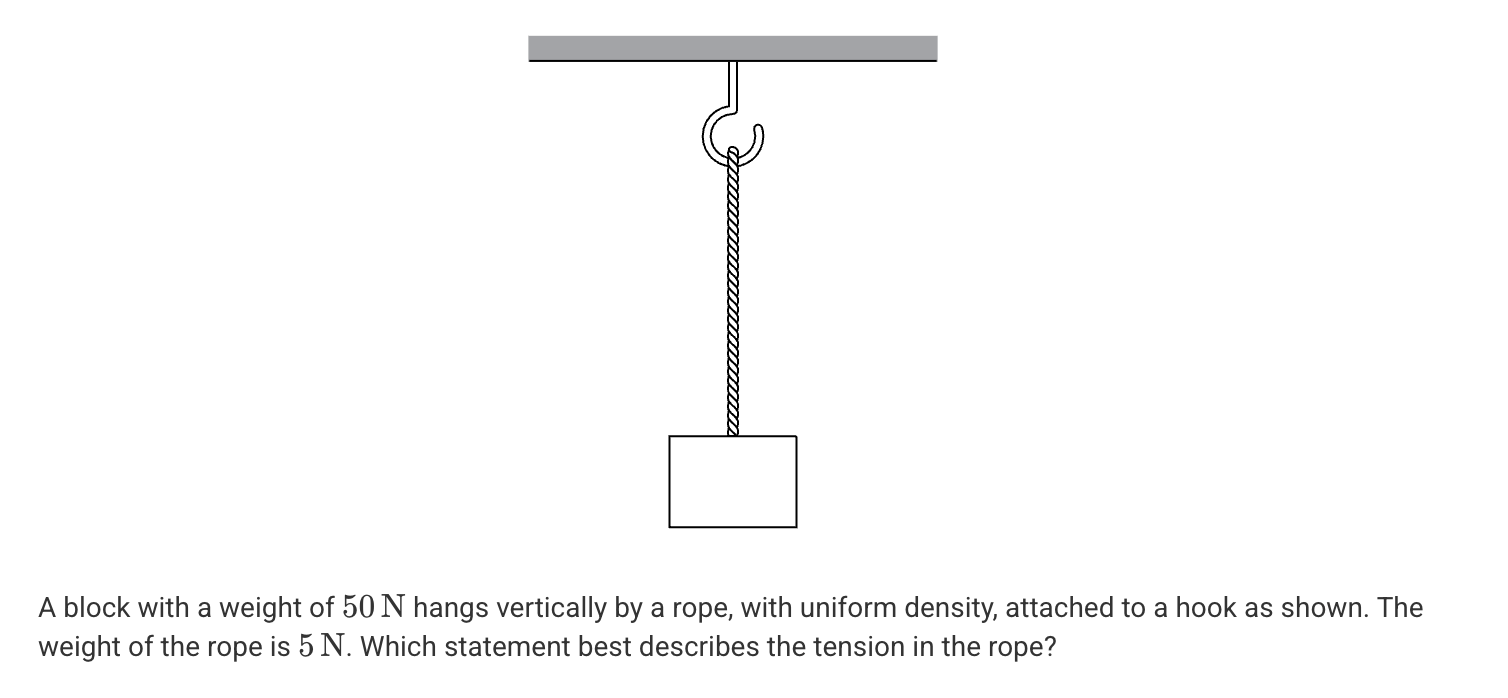
A. The tension in the rope is 50N at every location along the rope.

B. The tension in the rope is 55N at every location the rope.

C. The tension in the rope changes uniformly from 50N at the top of the rope to 55N at the bottom of the rope.

D. The tension in the rope changes uniformly from 50N at the bottom of the rope to 55N at the top of the rope.

D

A. |F₁| = |F₂|

B. |F₂| = |F₃|

C. |F₁| = |F₃|

D. |F₁| = |F₂| = |F₃|

C

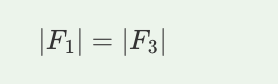
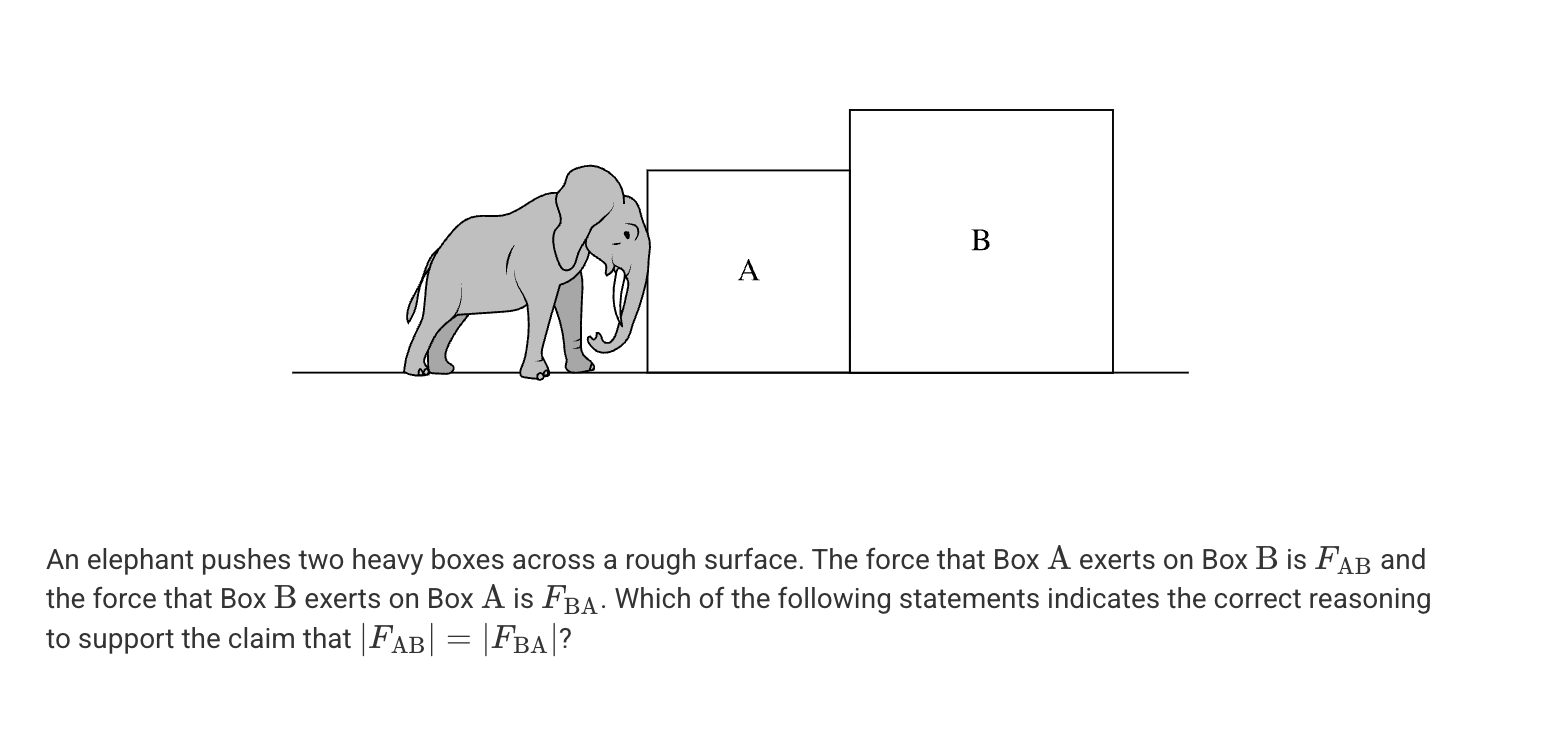
A. This claim is true only if the boxes are moving with a constant velocity.

B. This claim is true only if the masses are equal.

C. This claim is true only if the boxes have equal mass and are moving with a constant velocity.

D. This claim is true regardless of the type of motion or the relative mass of the object.

D

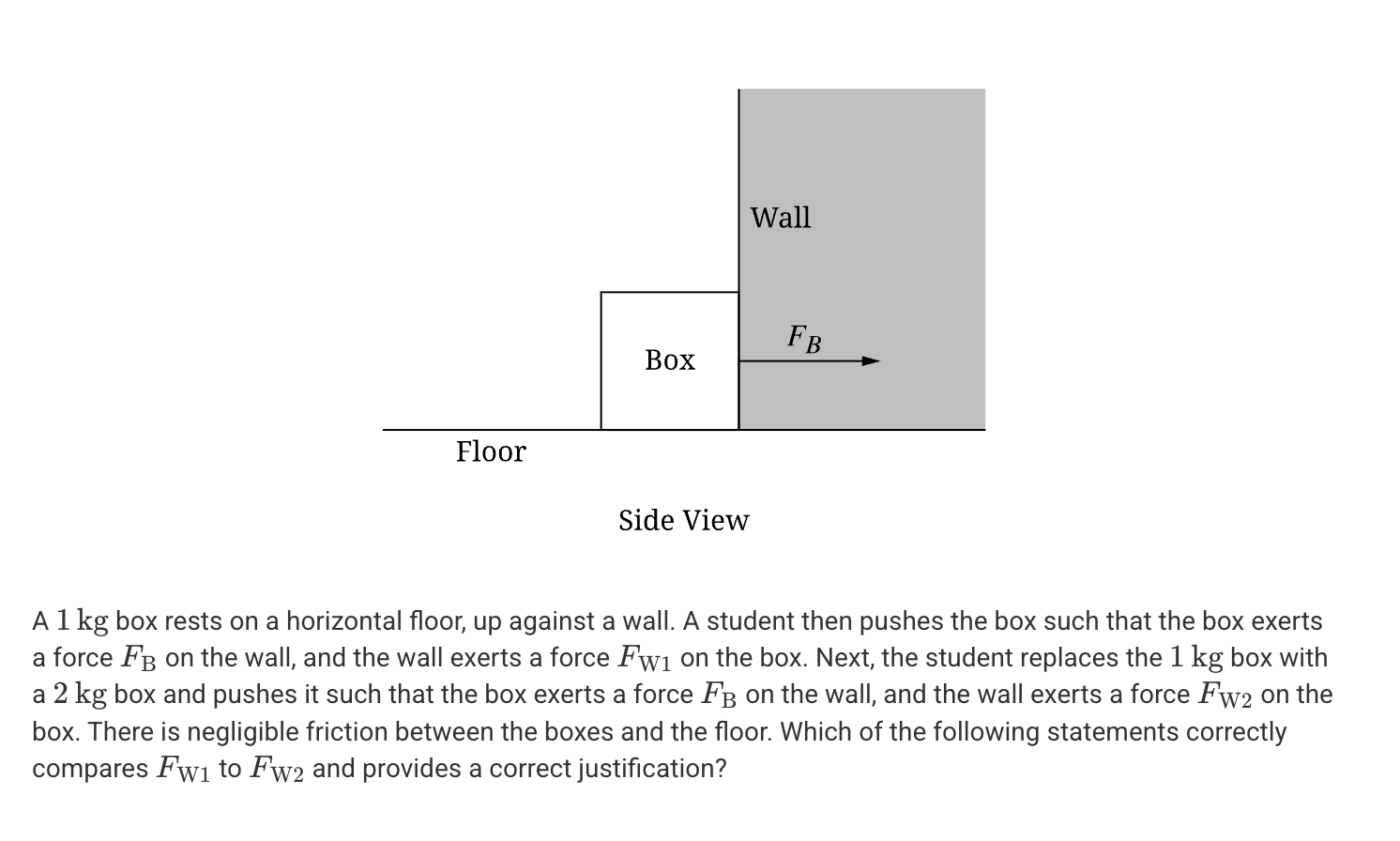
A. F_W2 > F_W1 because the weight of the 2kg box is greater than that of the 1kg box.

B. F_W2 > F_W1 because the normal force exerted on the 2kg box must be greater than the normal force exerted on the 1kg box.

C. F_W2 = F_W1 because the force that the wall exerts on the box has a magnitude of F_B in each case.

D. F_W2 = F_W1 because the force of friction is negligible in each case.

C

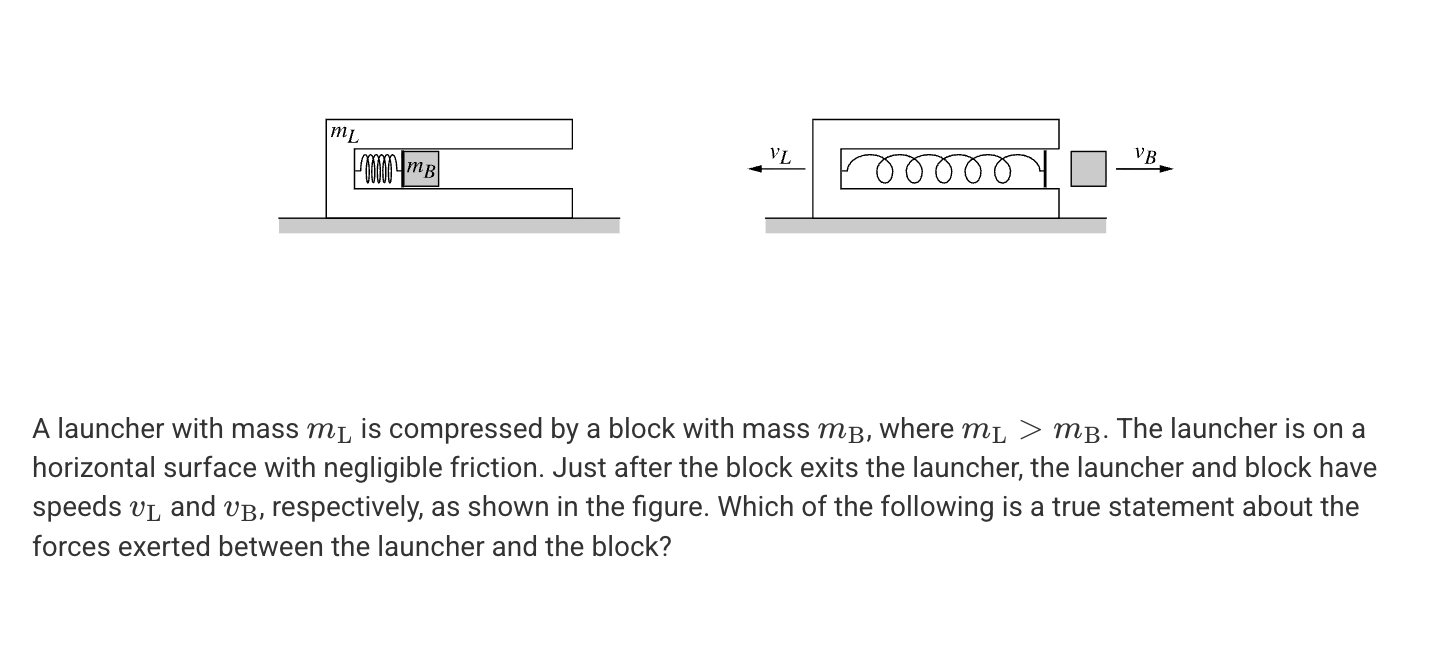
A. The launcher exerts a greater force on the block than the block exerts on the launcher.

B. The block exerts a greater force on the launcher than the launcher exerts on the block.

C. The block and the launcher exert forces of equal magnitude on each other.

D. The relative magnitude of the force exerted on the spring by the block and launcher cannot be determined without knowing and v_B and v_L.

C

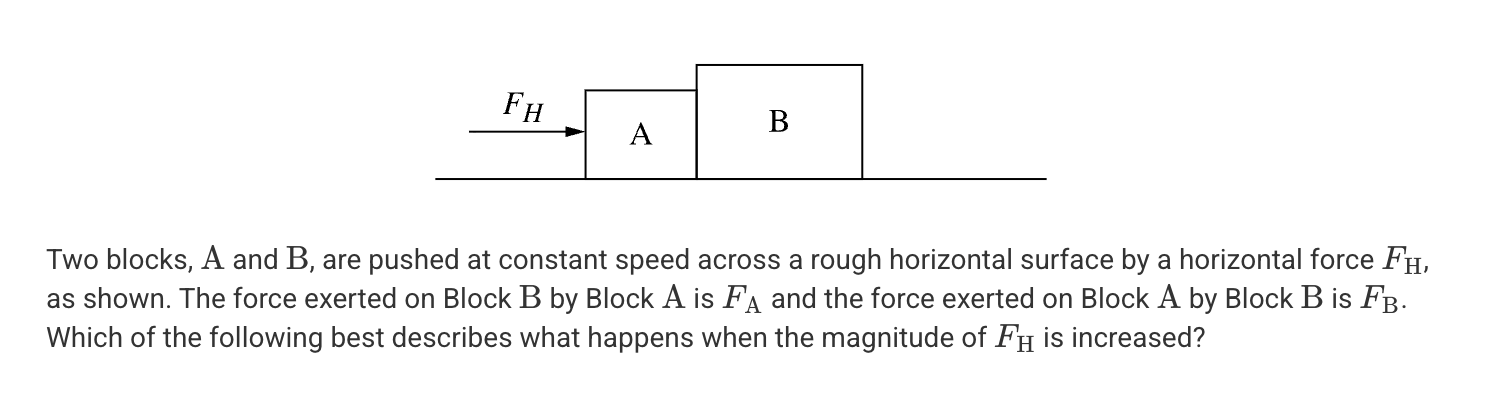
A. |F_A| would decrease and |F_B| would increase.

B. |F_A| would increase and |F_B| would decrease.

C. |F_A| is greater than |F_B|, but both increase as F_H increases.

D. |F_A| and |F_B| would both increase and would remain equal to each other

D

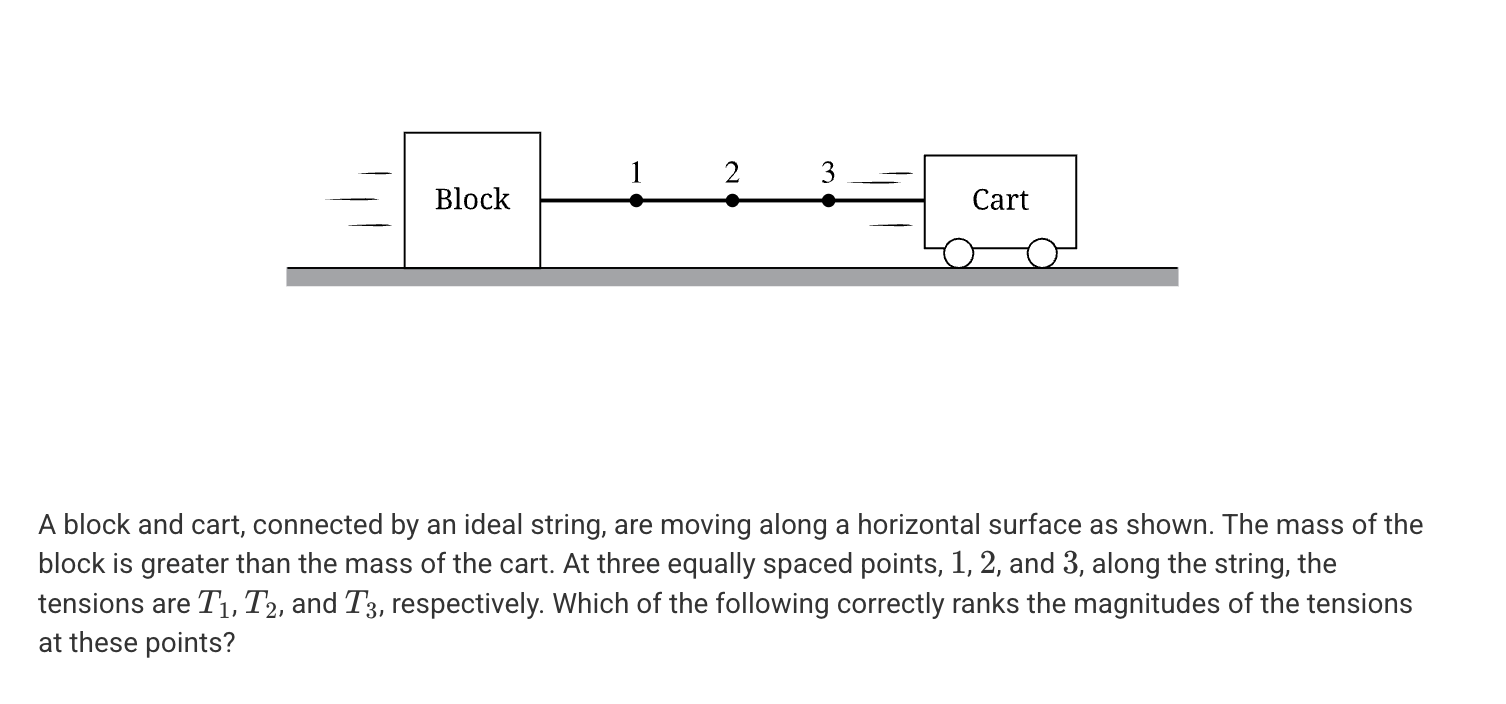
A. T₁ = T₂ = T₃

B. T₁ > T₂ > T₃

C. T₁ = T₃ > T₂

D. T₃ > T₂ > T₁

A

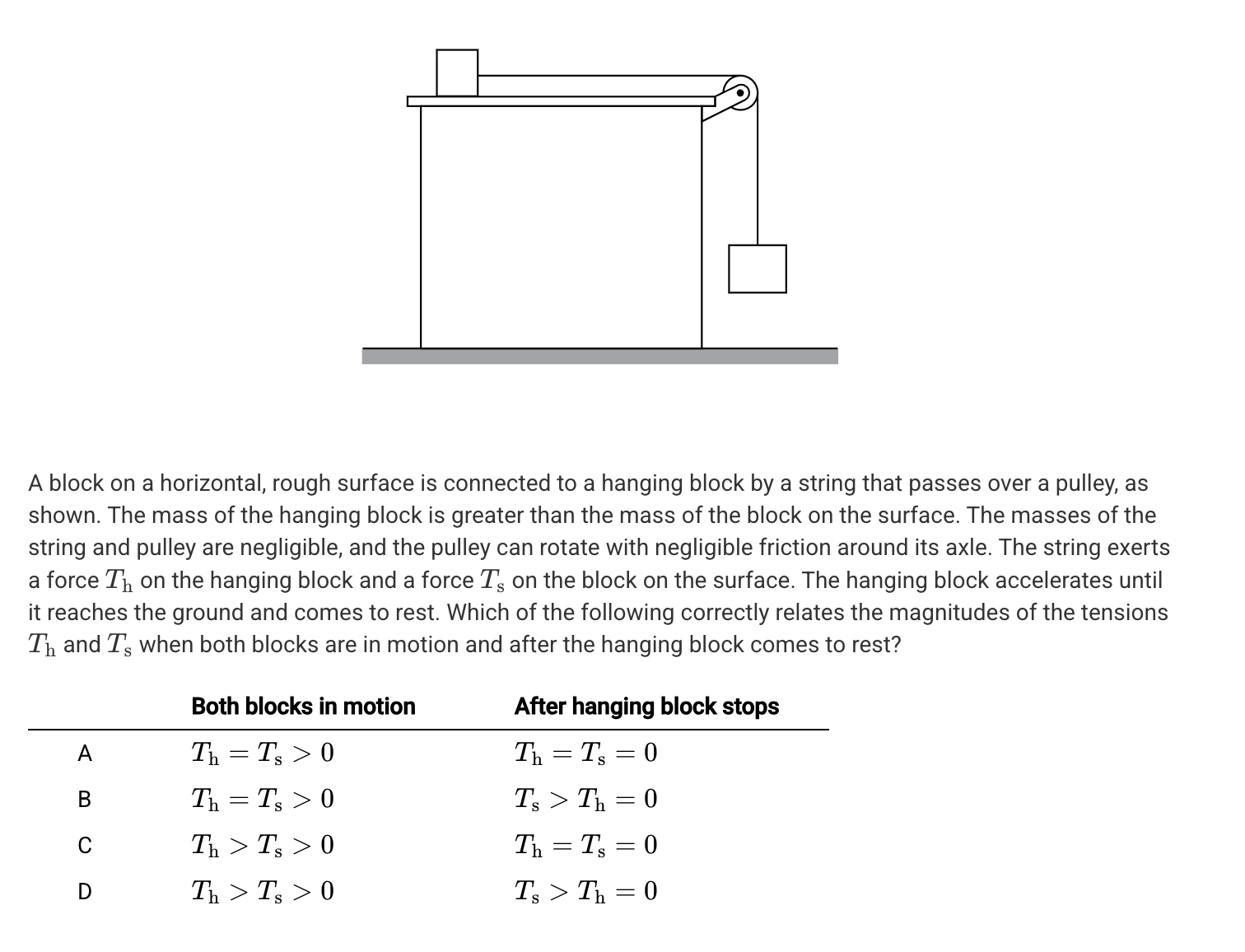
A.

B.

C.

D.

A