ap calc weak terms

The derivative of sinx

cosx

The derivative of cosx

-sinx

Integral of sinx

-cosx

Integral of cosx

sinx

1 + tan²x =

sec²x

1 + cot²x =

csc²x

cos(2x)=

cos²(a)-sin²(a)

sin(2x)

2cos²(a)sin²(a)

arctan(sqrt3)

pi/3

arctan(sqrt3/3)

pi/6

ln(0)

undefined

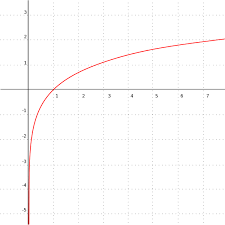
graph of ln(x)

Definitions of a limit

A function f has a limit at x = a if and only if the limit as x approaches a from the left = the limit as x approaches a from the right, so there are no discontinuities/jumps/breaks in the graph of f(x).

Critical point

the number x = a is a critical point of f if and only if f’(x) = 0 or undefined

lim x→0 sinx/x

1

lim x→0 cosx-1/x

0

The Intermediate Value Theorem

If f is continuous on [a,b], for any value L between f(a) and f(b), there exists some c` where f(c) = L.

The Mean Value Theorem

For any function continuous on [a,b] and differentiable on (a,b), there exists some point c on (a,b) such that f’(c) = the average rate of change of f. AKA, f’(c) = [f(b)-f(a)]/b-a

L'Hopital's rule

If f and g are differentiable and the limit as x→a of f/g = 0/0, infinity/infinity, or some similar combination, then the lim x→a f/g = limx→a f'/g’

d/dx [f^-1x]=

1/f’(f^-1x))

d/dx a^x

a^x lna

d/dx ln|x|

|1/x|

d/dx [log_bx]

1/ln(b) * 1/x

f has a local maximum at x=a if

f’ goes from positive to negative at x = a, or if f’=0 and f”<0.

Definition of a definite integral

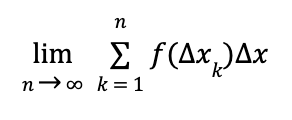
The Fundamental Theorem of Calculus

If f is continuous on [a,b], then:

FTC1 with Chain Rule

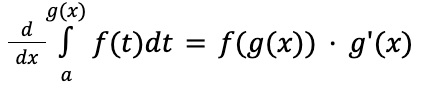
The Mean Value Theorem (for Integrals)

If f is continuous on [a,b] and differentiable on (a,b), there exists some c where f(c) = the integral from a to b of f'x dx * 1/b-a, or the instantaneous change of f = to the average rate of change of f.

speed

|v(t)|

displacement

integral from a to b of v(t)/ x(a)-x(b)

total distance traveled

integral from a to b of |v(t)|

x(t_f)

Initial position + the integral of velocity (initial position + displacement)

average velocity

integral from a to b of v(t) / b-a