Trig unit 2

Special Angles

2 types of triangles that have the angles, 30°(x1), 60°(x1), 45°(x2)

'First' Type of Special Angles(there isn't really types but this is a way to remember)

45° + 45° + 90°

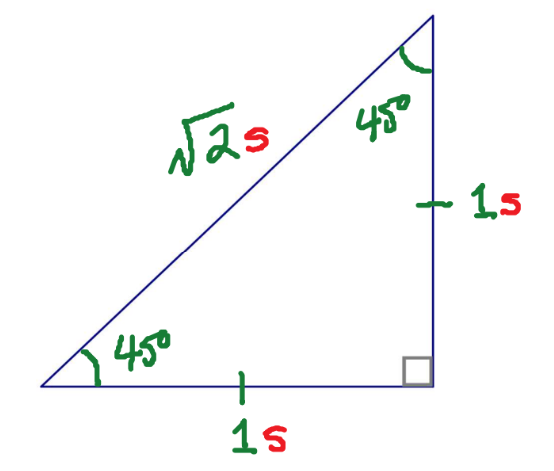
Special Numbers for ‘First’ Triangle

1, 1, √2

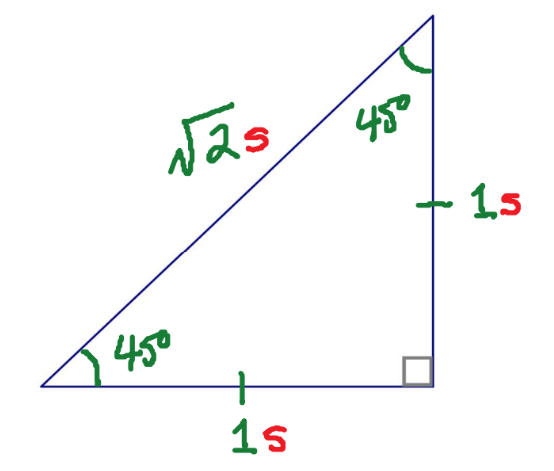
Trigonometric Ratios for the ‘First’ Triangle

Sin 45° = 1/√2 or √2/2

Cos 45° = 1/√2 or √2/2

Tan 45° = 1/1 or 1

‘Second’ Type of Special Angle

30° + 60° + 90°

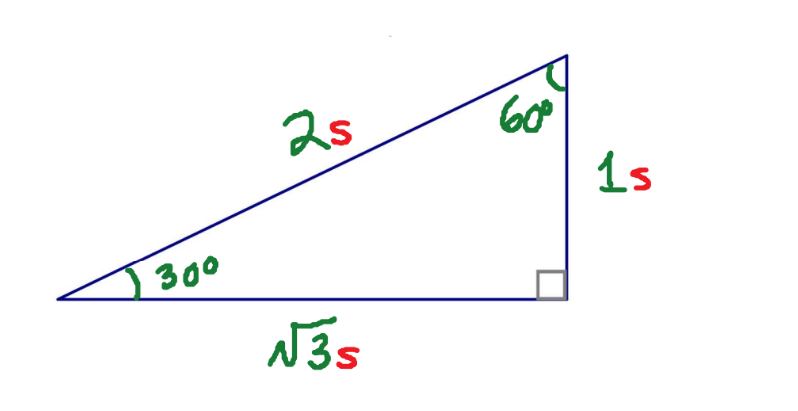
Special Numbers for ‘Second’ Triangle

2, 1, √3

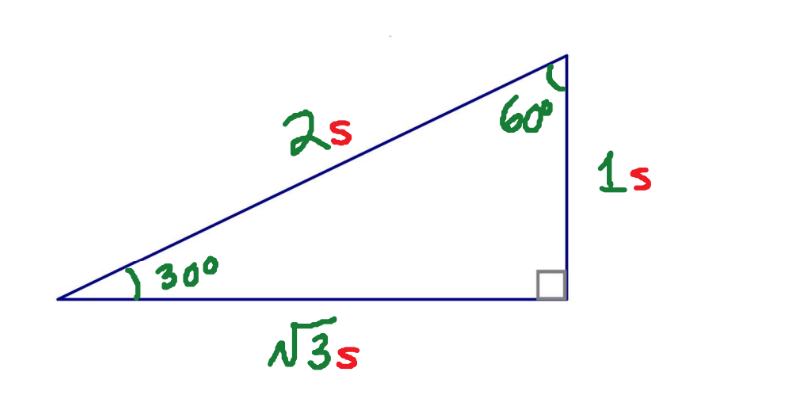
Trigonometric Ratios for the ‘Second’ Triangle, angle 30°

Sin 30° = 1/2

Cos 30° = √3/2

Tan 30° = 1/√3 or √3/3

Trigonometric Ratios for the ‘Second’ Triangle, angle 60°

Sin 60° = √3/2

Cos 60° = 1/2

Tan 60° = √3/1 or √3

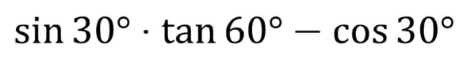
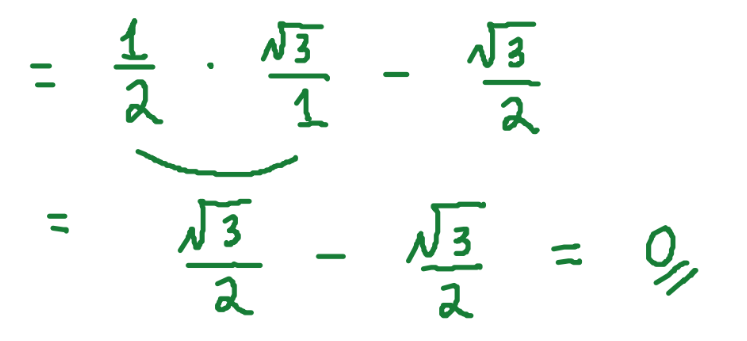
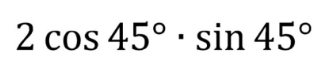
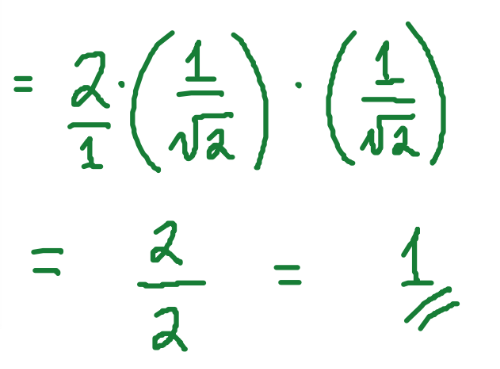
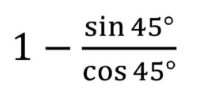
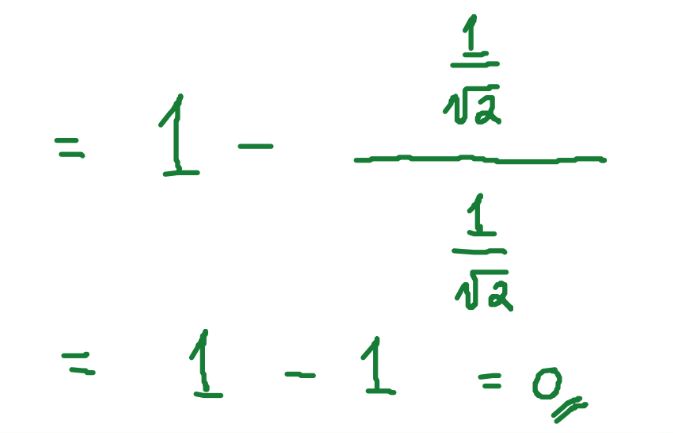
Lesson One Done!

On to Lesson Two!

Standard Space

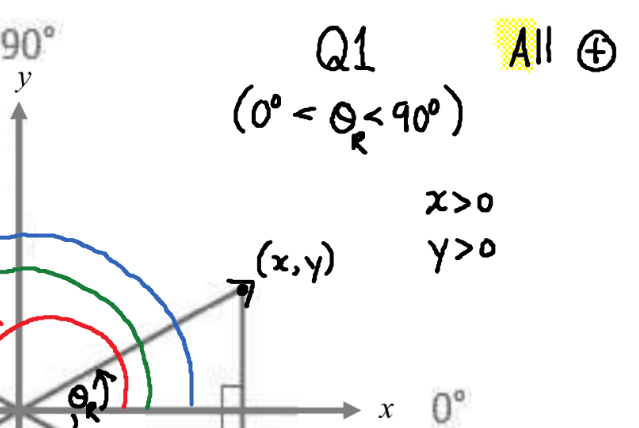
When it’s Initial Arm is on the Positive x-Axis, and the origin is (0,0), Otherwise known as Q1!

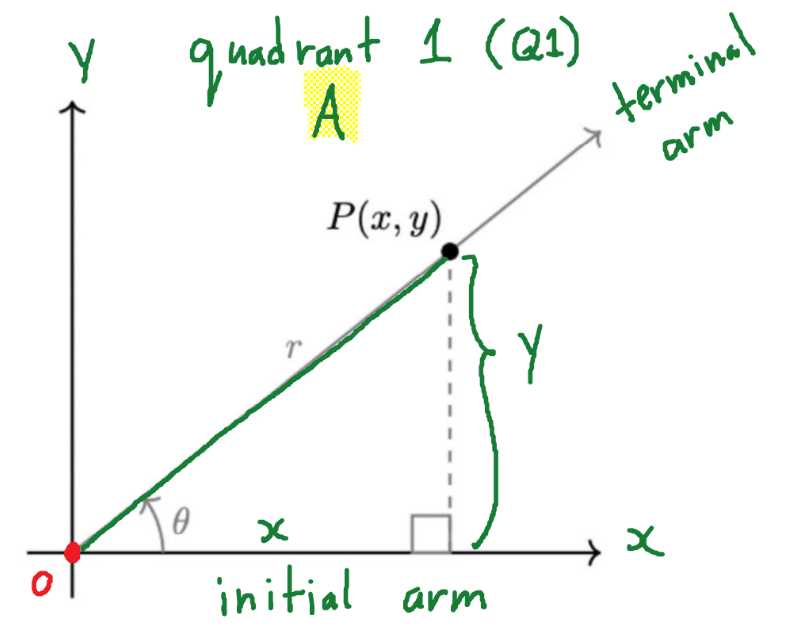
Terminal Arm

It Contains Coordinates(x,y) that Define the Angle and the Triangle.

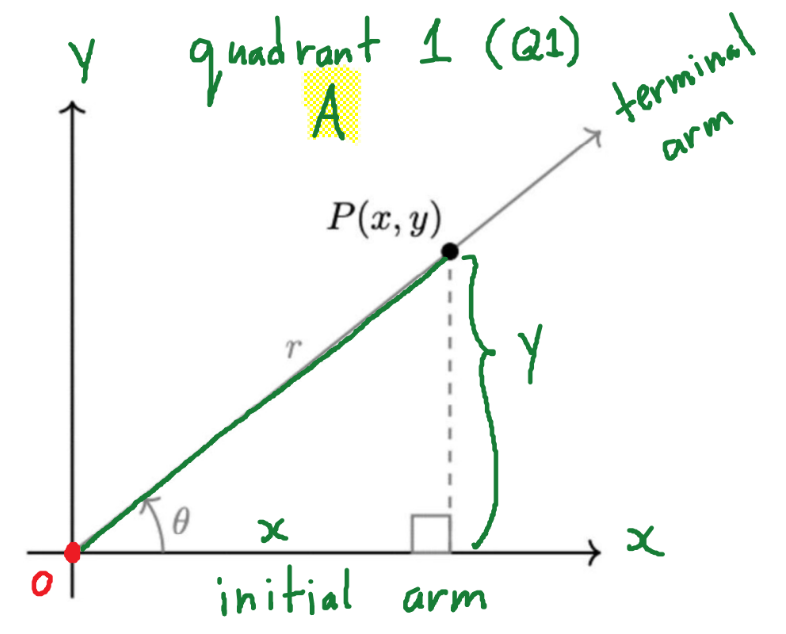
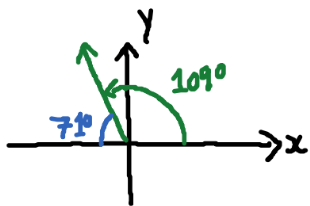
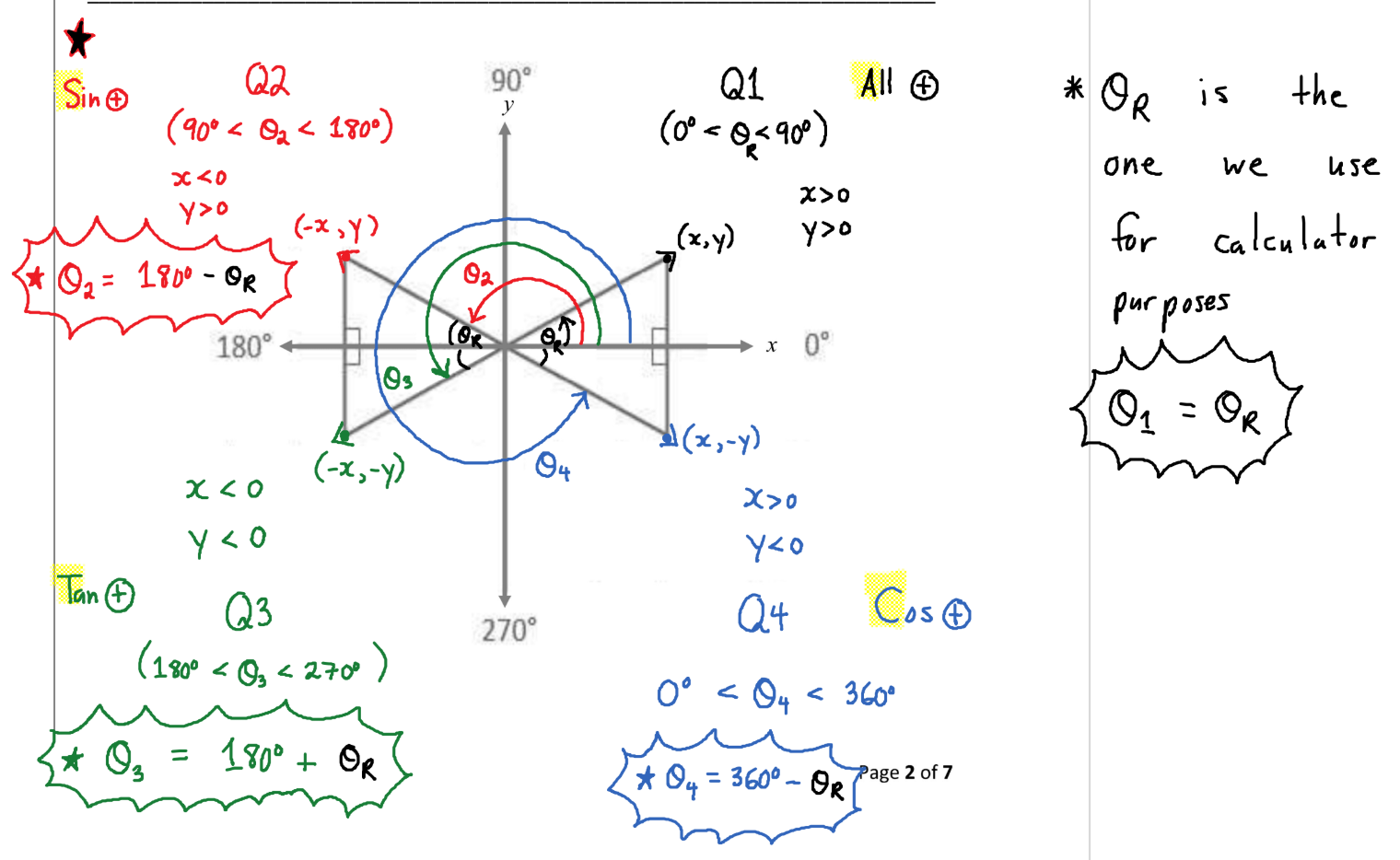
Related Angle

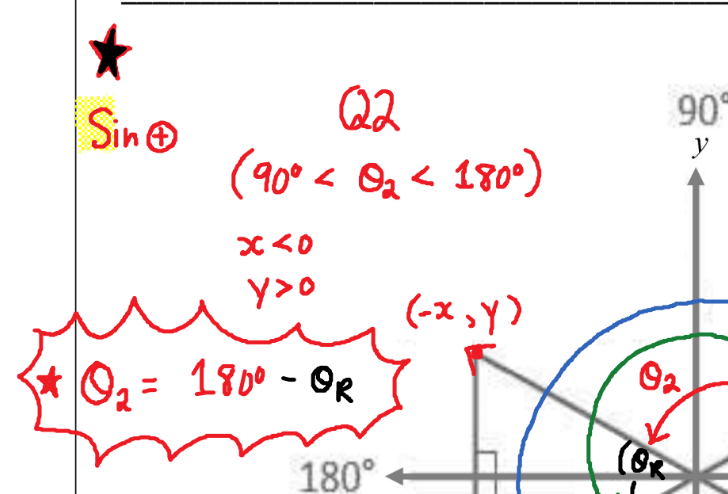
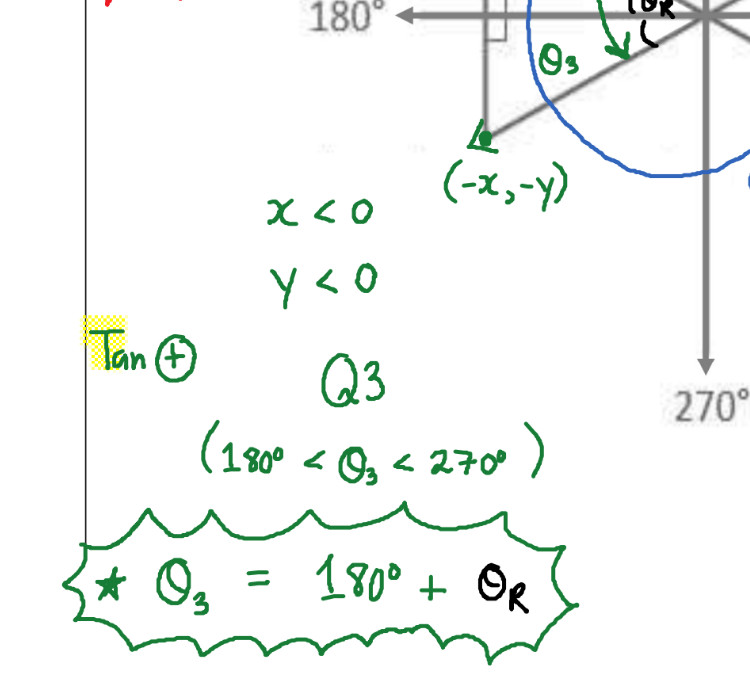
The Acute Angle(Less than 90°) Formed by the Terminal Arm of an Angle(In Standard Position) and the Nearest X-axis. The Related Angle to θ(Theta) can be Denoted as θ_R. In This Case Blue Would be θ_R.

Lesson Two Done!

On to Lesson Three!

r (Radius, a side length)

√x² + y²

(This is the Pythagorean Formula)

Sine θ

y/r

Cos θ

x/r

Tan θ

y/x

Q1, A

Q2, S

Q3, T

Q4, C

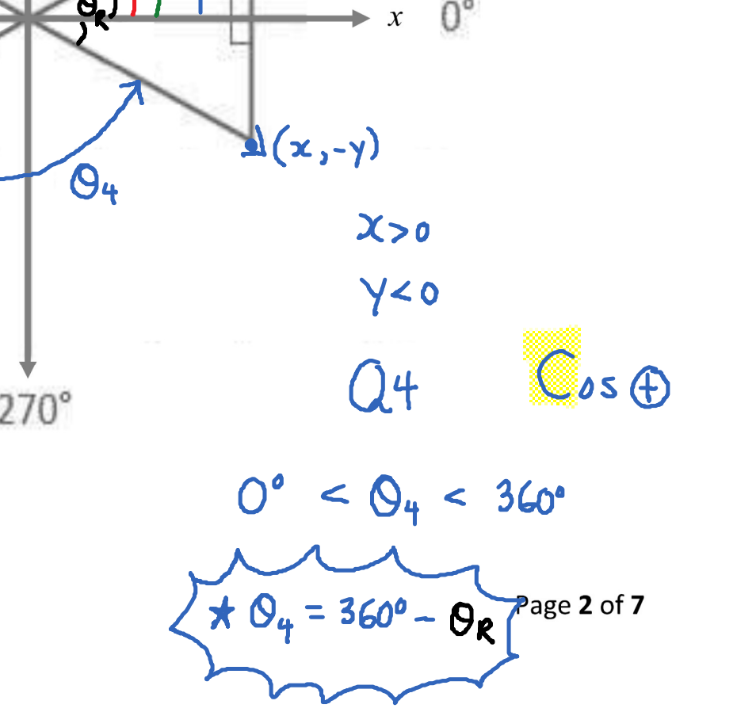
CAST

Co-Terminal Arm

Angles that share the same arm, ie. 200°, if you add 360° it is in a new Quadrant but still the same?

Co-Terminal Arm, Formula

Lesson 3 Done!

On to Lesson 4!

Inverses

When you remove the Function from the Angle, they help find angles ex. y = Tan^-1(x)

Reciprocals

When you flip the Ratio to another Ratio

Cosecant

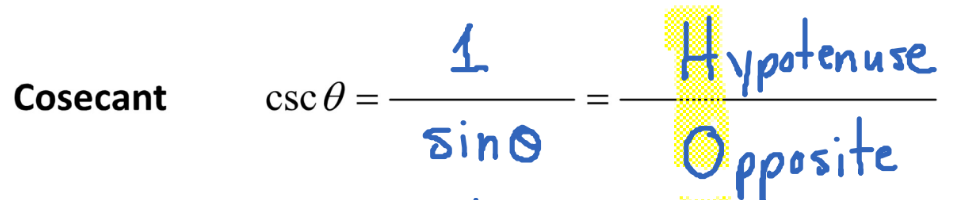
Secant

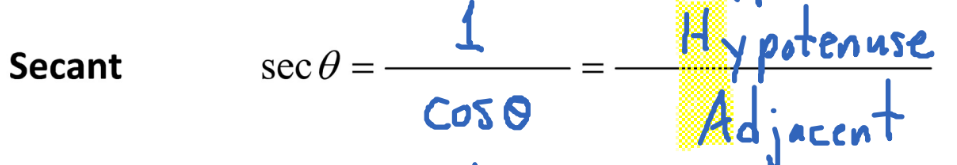
Cotangent

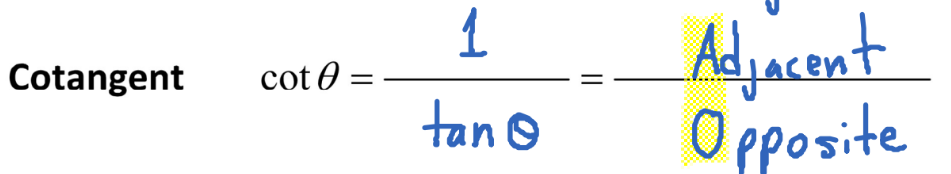
Reciprocal SOH CAH TOA

SHO CHA TAO

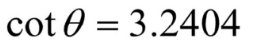
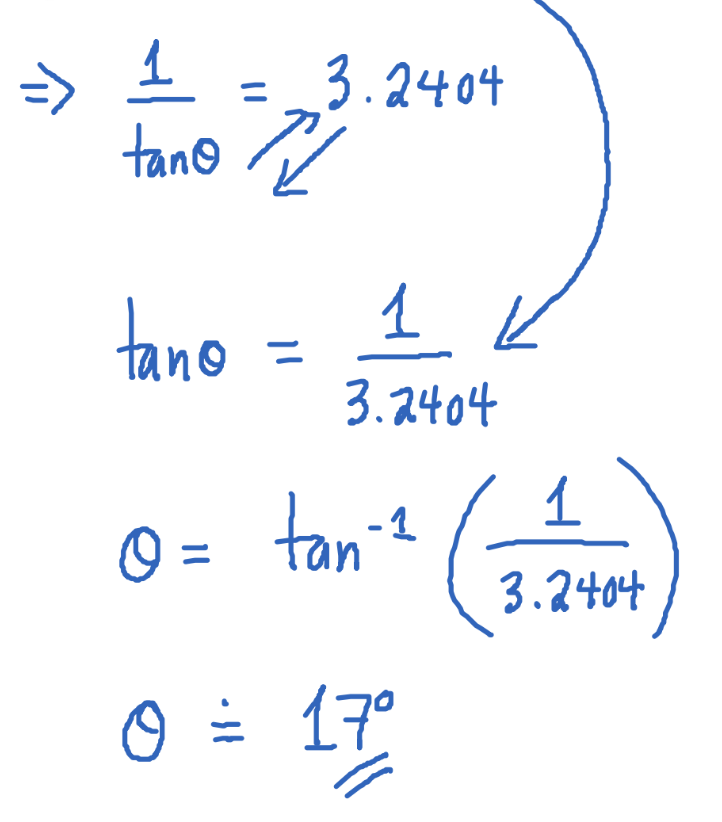
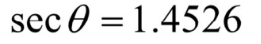
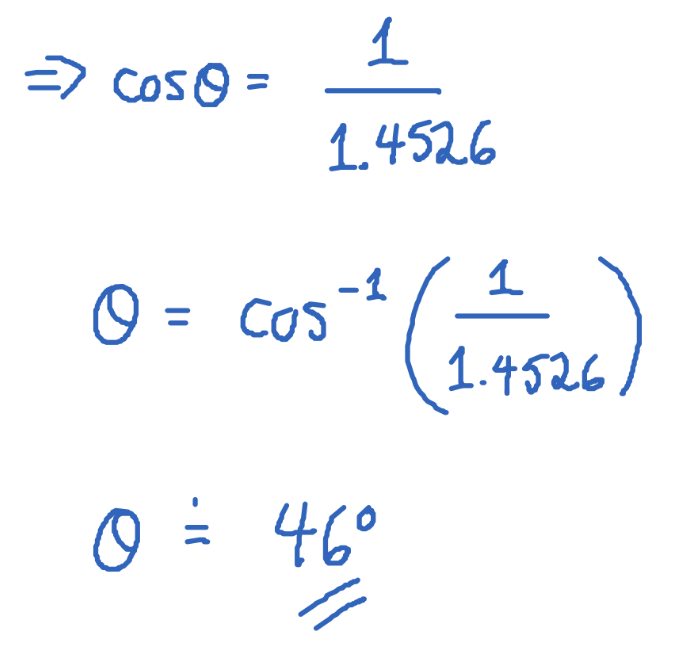
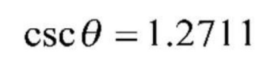
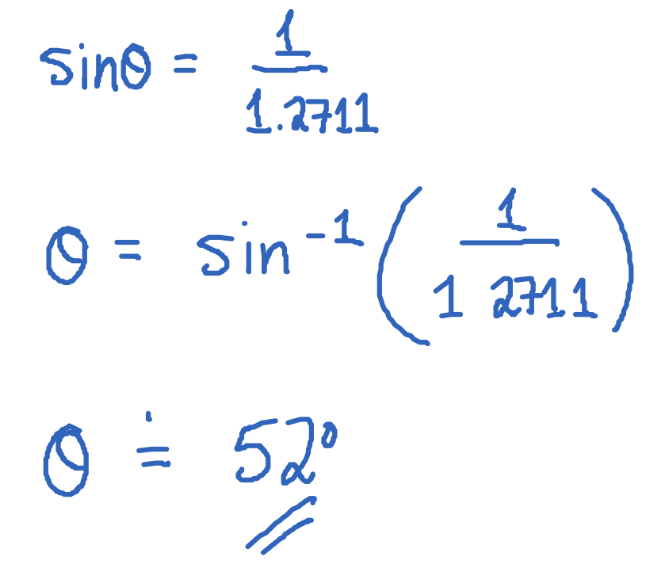
Lesson 4 Done!

On to Lesson 5!