Inorganic Lecture 15 - Lattices/Crystal Structure

test review

"z axis between two atoms"
clay triangle. have a perp C2 but not a sigma h

1

2 types of solids:
1. Amorphous
-lacking a regular arrangement of atoms
--may be pockets that are very ordered then right next door very ordered
-Lack large structural order
-Properties vary. wide range of melting because of differences. some parts of it melt and lower, some at higher.
2. Crystalline
-Atoms/ions/molecules in regular, repeating pattern
--minimizes free energy
---in a crystal everybody is as happy as they can get
-Unit cell is smallest repeating unit and has the same symmetry as the overall crystal

Amorphous ex. Glass
Crystalline ex. quartz

2

Crystalline solids:
Ionic
Covalent network aka "covalent crystals" or "network crystals"
-atoms bonded throughout
Molecular
-sugar crystals; discreet molecules
Metallic
-just metals; alloys
(frozen noble gases, we won't really talk ab just cool)

3

7 sets of crystal systems:
1. Cubic
2. Tetragonal
-only one side is different
3. Orthorhombic
-all sides different
we'll ignore monoclinic, triclinic (angles and side lengths different), and rhombohedral
7. Hexagonal

Cubic and Tetragonal are Orthorhombic. But Orthorhombic is not cubic or tetragonal.

Three of them fit into just two of those systems [?]
Primitive=simple cubic
Body-centered cubic
Face-centered aka Cubic Close Packing (CCP)
Hexagonal Close Packing (HCC)

Only polonium forms simple cubic.

4

Lengths of unit cell edges are called lattice constants
For cubic, a=b=c, so only have 1 really
3 Cubic's:
1. Simple cubic: one in every corner
2. Body-Centered Cubic
3. Face Centered Cubic

5

Simple cubic. 1/8 in every corner. 1/8 occupancy*8 atoms = 1 total atom
Body center: 1 in middle, 1 from corners = 2
Face: 1/2 * 6 faces + 1 atom from corners = 3+1 = 4 atoms

Corner = 1/8
Face center = 1/2
body center = 1
Edge center = 1/4

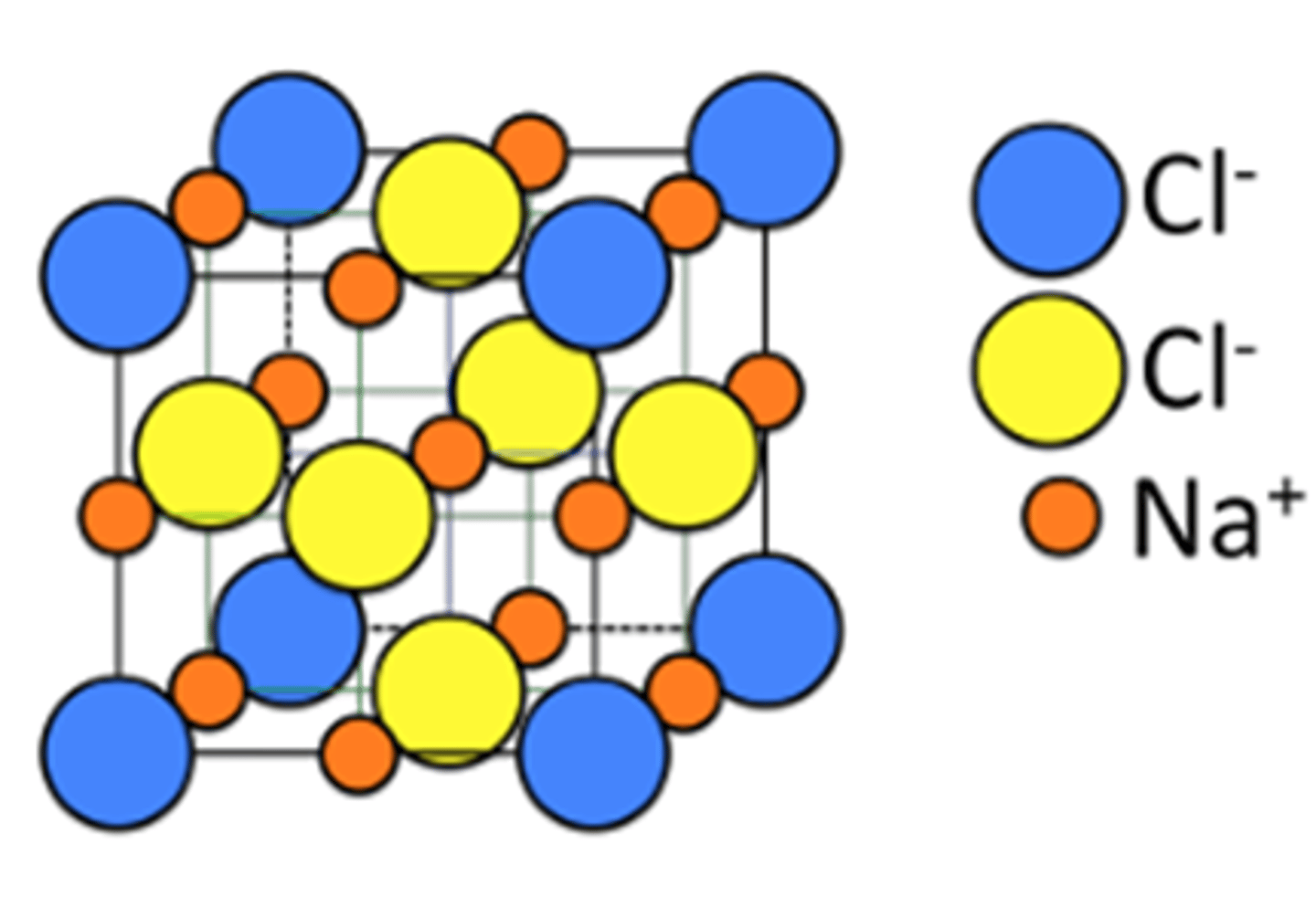
NaCl
Each ion (Na and Cl) form their own sublattices that are FCC
If this is one unit cell, how many of each atom are present (picture)
Cl-
8 corners = 1
6 faces = 3
Na+
12 Edge center = 3 [look at middle row!]
1 body center = 1
Unit Cell: 4 (Na+Cl-)

6

get trend that simple cubic is less efficient in terms of volume occupied vs volume present
FCC is most efficient in packing
Coordination number also goes up with increased packing efficiency.

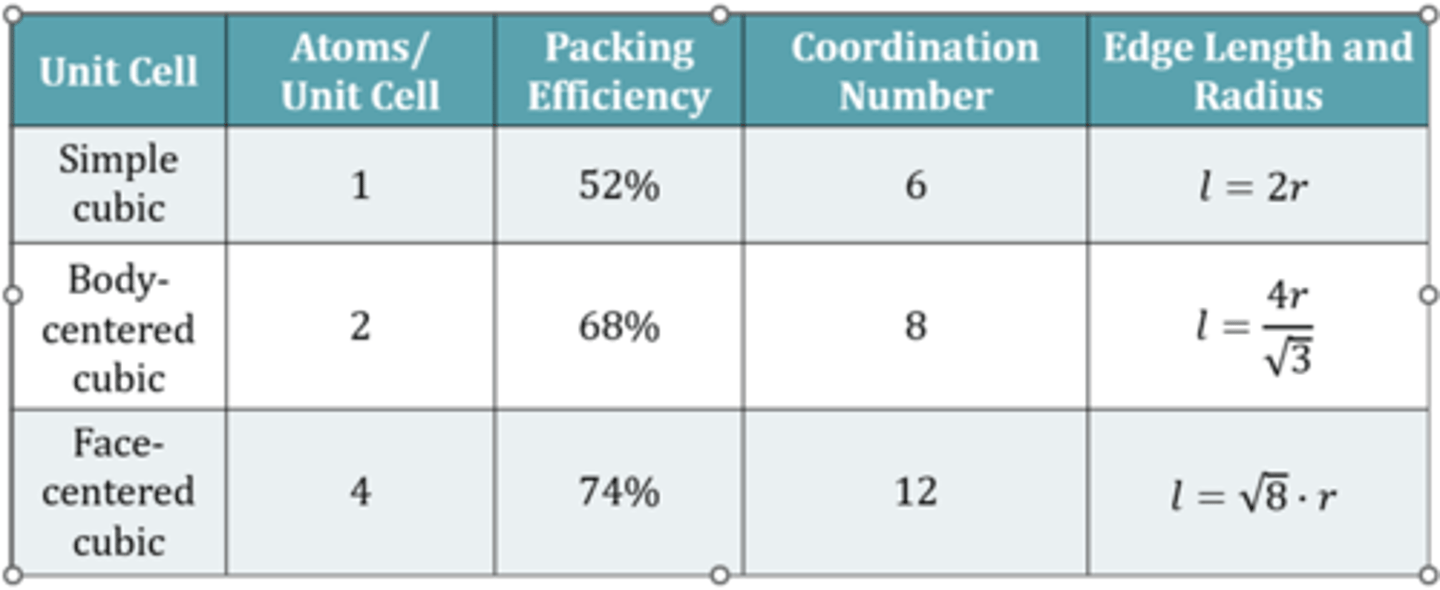
7

Simple cubic. edge length is sum of two atom radii.

BCC. atoms at corner no longer touch. atoms at corner, though center, to next corner that touch.
-so we draw a triangle with hypotenuse from bottom left to top right. gives hypotenuse as 4r. we need to find edge length.
-so draw second triangle.
system of equation.

FCC: front corners and middle face touch. so hypotenuse is r+2r+r. so then (4r)^2 = l^2 + l^2
4r/sqrt(2) r = sqrt(8)r

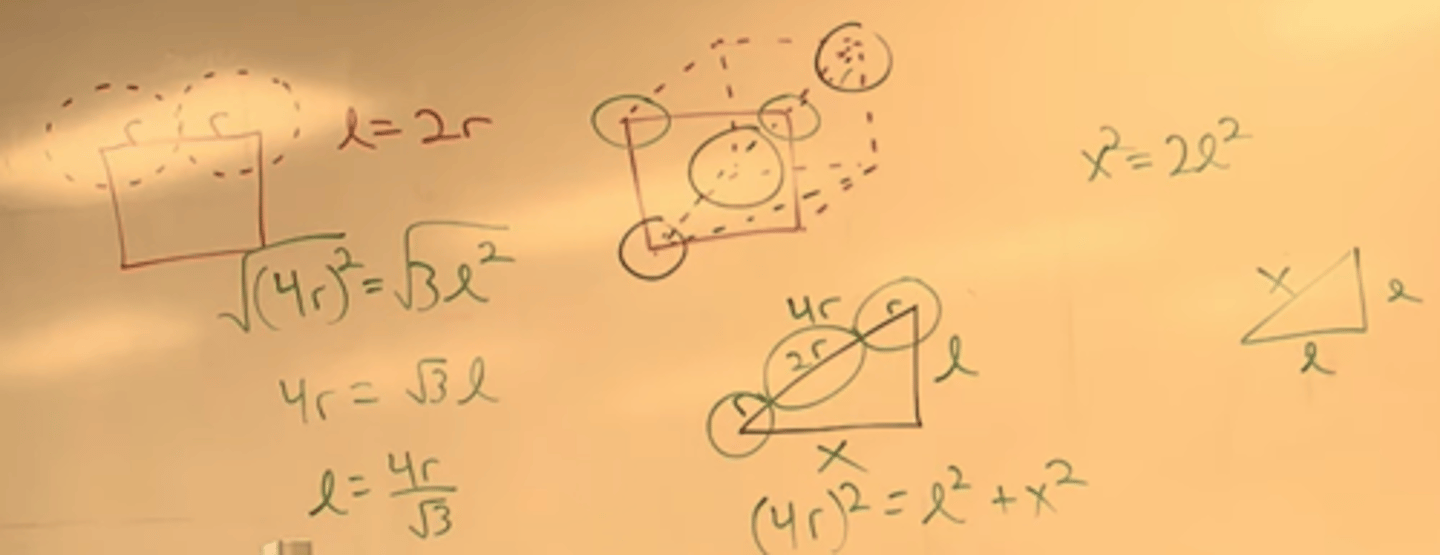
8

V of Mn atom is 9.21E-24 cm^3. FCC. Density=?
Use V of Mn to get radius using V=4/3 π r ^3 (integral of SA)
[?amu and grams conversion]
V=l cubed.
atoms/cell -> mass/Volume
Given density and unit cell, get radius or volume. much more practical.

9

recap. how many atoms/cell. edge in terms of radius. V occupied. (simple cubic, V = (2r) ^3

10

Na Cl
What is the coordination number of Na+? 6
Na+ radius is 116 pm. Cl- radius is 167 pm.
Determine edge length and volume of unit cell.
FCC, using diagonal of front face. rCl + [?should be (2167 + 2116) = l. then V = l^3 /me: Cant do diagonal bc Cl- nit touching

11

In one unit cell there's 1Cl and 1Cs. So CsCl
"4r" value in FCC equation is equal to "2(rCl) + 2(rCs)"
Substitute and solve

12

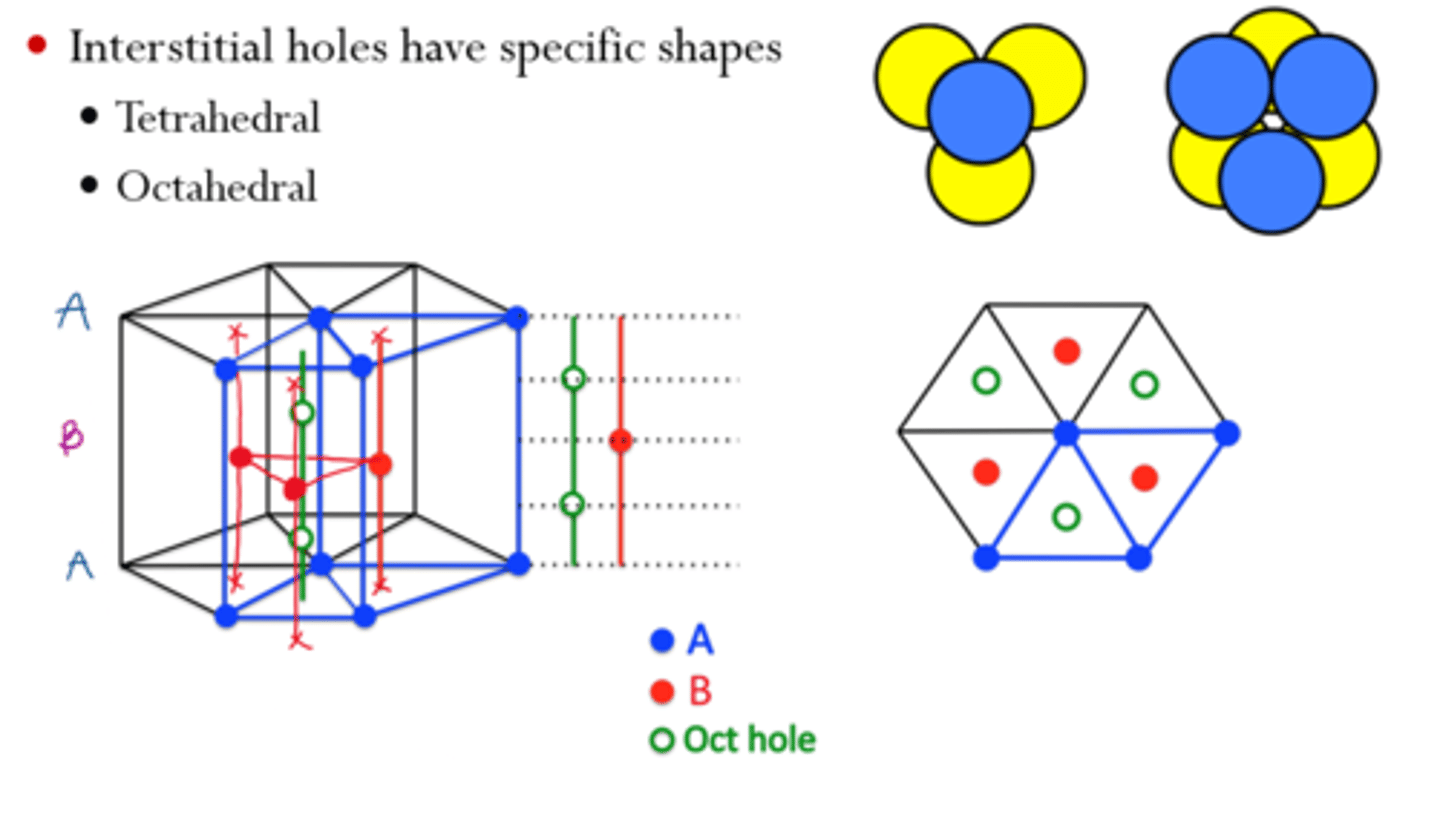
In FCC lattices, there are holes
-Tetrahedral holes: in every quadrant of the unit cell, so a total of 8.
-Tetrahedral /Oh?/ holes: edge centers and body centers
Na and Cl form FCC lattices, occupying each others octahedral holes

CaF2
Put Ca2+ ions in every corner and face centers
Then put fluoride in tetrahedral holes
Ca2+: corners=1 ; face centers=3
When occupying holes, entire atom is there
so for F-: tetrahedral holes: 8 atoms
2:1 ratio F:Ca

Another word for these holes: interstitial holes

13

Close-packed structures: most efficient possible structures we can make
-consider taking incompressible spheres and packing in box
-First layer would form 2D hexagonal array. One in middle with six neighbors around
--Center would have a coordination number of 6
Then start stacking 2D arrays
This is cubic close packing
(irregular close packing would lead to amorphous)

Hexagonal Close Packing
- close-packed structures with sequence: ...ABABAB...
-- 1st layer: 2D array (A)
-- 2nd layer: 2D array placed on the holes (B)
--3rd layer: directly above first (layer A repeat)
---1st and 3rd layer line up
Often drawn as a hexagonal prism
[Hexagonal prism is of A layers. B layer atoms would be in center of A triangles]
Coordination number of 12 [triangle below=3, triangle above=3, hexagon around that atom=6]
[?(when all atoms are the same)]

HCP has its holes
-Tetrahedral (left)
-Octahedral (right)
Many metals take HCP

Cubic Close Packing; another name for Face Centered Cubic, just that we turn our view. Instead of thinking of it as a cube, we look at it from the corner of the cube, we get cubic close packing where layer C instead of being directly over A, is in its own spot. A and B are just like in Hexagonal, but 3rd layer (C) is shifted next over. can still only do alernating holes, but shifted over. Fourth layer back to A.

[?picture]