Calculus: Antiderivatives, Riemann Sums, and Derivative Rules

Antiderivative

We say the function F is an antiderivative of the function f if F'(x)=f(x)

Indefinite integral

The collection of all antiderivatives of f(x) is the indefinite integral

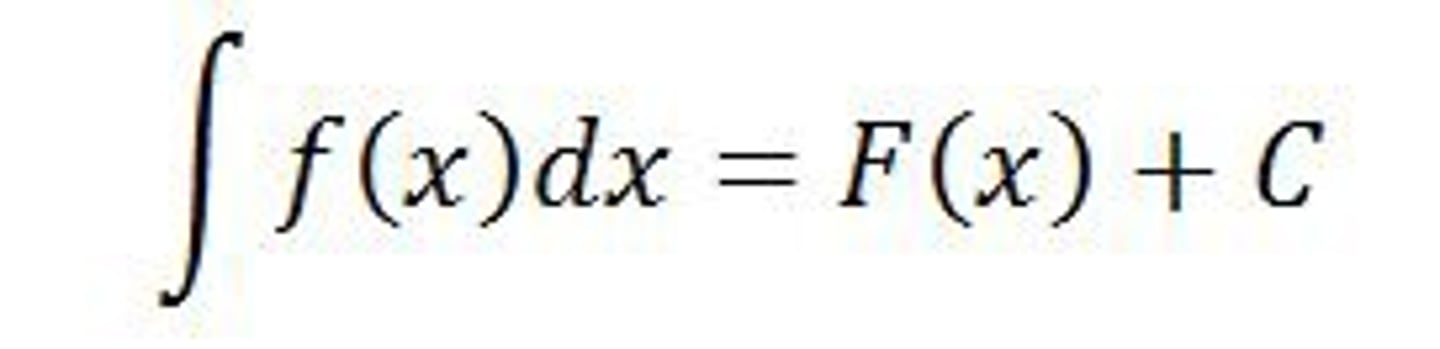
Riemann Sums

Approximation of area under curve using rectangles.

1. Break the interval [a,b] into n subintervals, and draw a rectangle in each subinterval.

2. Summing the areas of the rectangles will approximate the area under the curve.

Riemann Sum Rectangle Width Formula

Δx = (b - a)/n

Where b is the rightmost limit in interval [a,b] and a is the leftmost limit, and n is the number of subintervals.

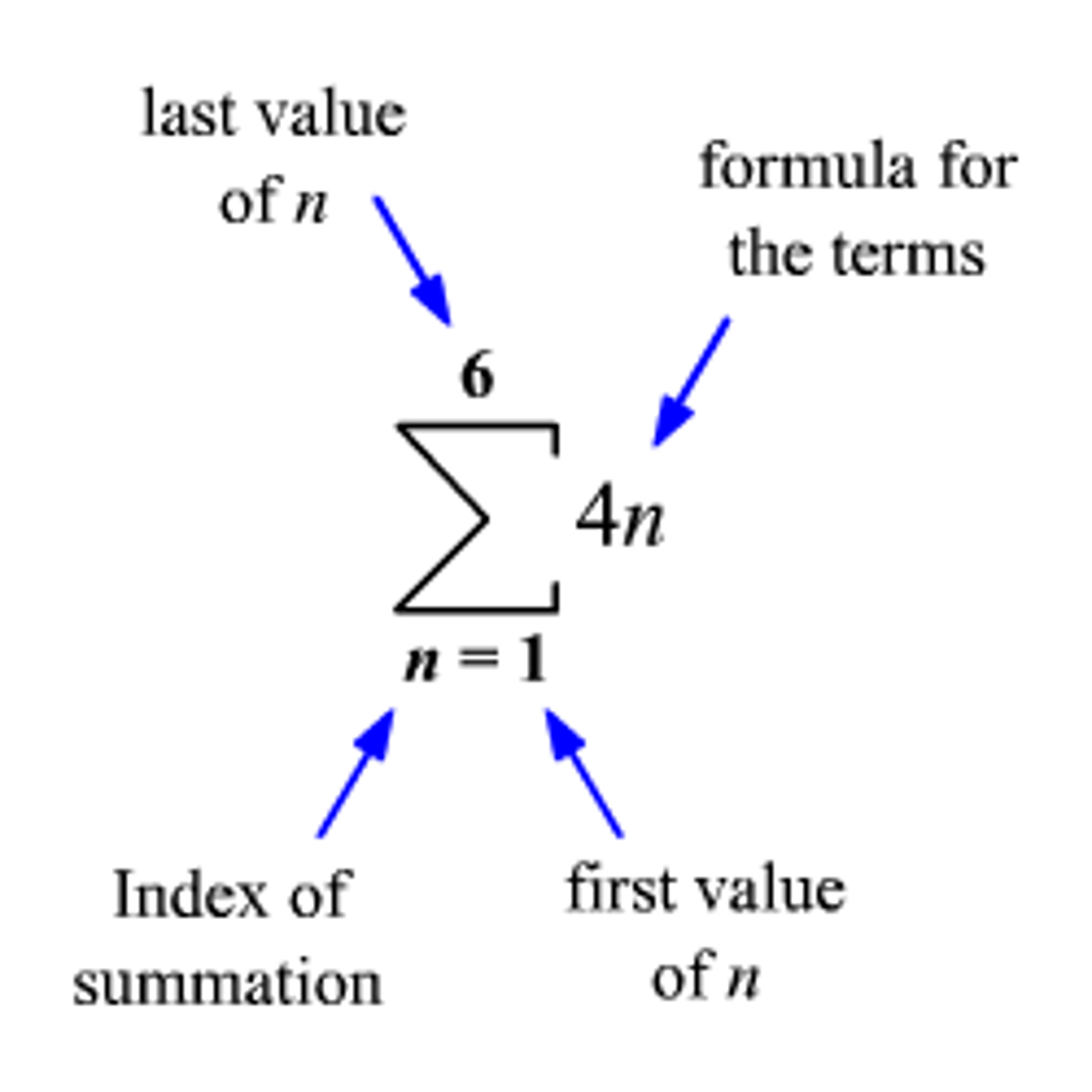
Sigma Notation

A form of notation using the symbol Sigma, to express a series.

Σ (Sigma symbol): Represents the sum of terms. Pronounced "sigma."

Index of summation (e.g., i): The variable used to count the terms in the sum. It changes values stepwise.

Lower limit (e.g., i=1): The starting value of the index, where summation begins.

Upper limit (e.g., n): The ending value of the index, where summation stops.

General term (expression next to Σ): The formula that describes each term in the sum depending on the index.

Upper Estimate Riemann

use rectangles that over-approximate the area

Let Mi = max{f(x)} on [xi-1, xi]

Then: Uf = nΣi=1 MiΔx

Lower Estimate Riemann

use rectangles that under-approximate the area

Let mi = min{f(x)} on [xi-1, xi]

Then: Lf = nΣi=1 miΔx

Midpoint Estimate Riemann

On the subinterval [xi-1, xi], the midpoint is (x_i-1 + x_i)/2

And the midpoint sum is:

Uf = nΣi=1 (x_i-1 + x_i)/2Δx

Average Value

AV = Area/b-a

Definite Integral

We define the definite integral to be the limit of the Riemann Sum

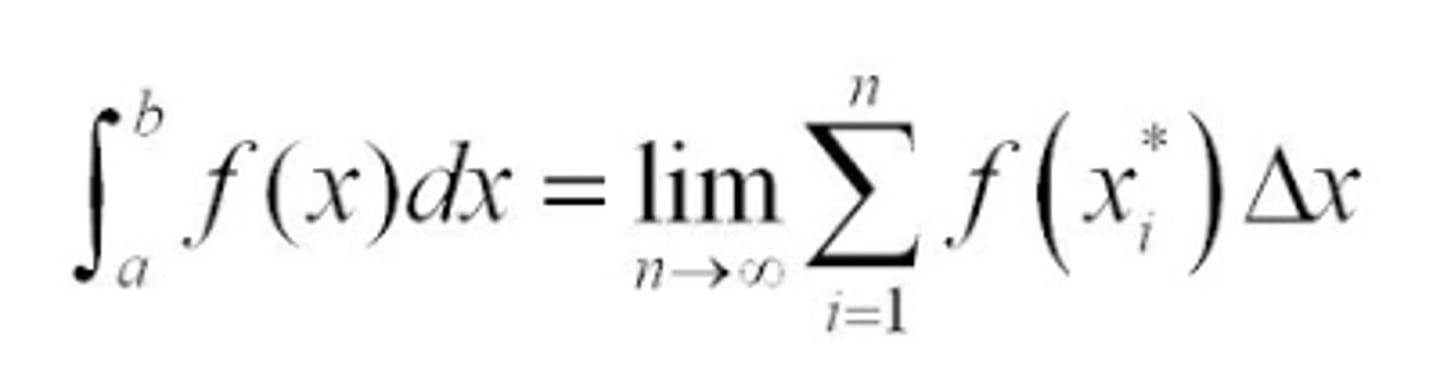
Summation Formulas

Odd and Even Integrals

If f is an odd function, integral between -a and a is 0

if f is an even function, integral between -a and a is 2 times the area

Trapezoidal Rule

Integral (a to b) = ((b-a)/2n)(f(x)+2f(x)+2f(x)+f(x))

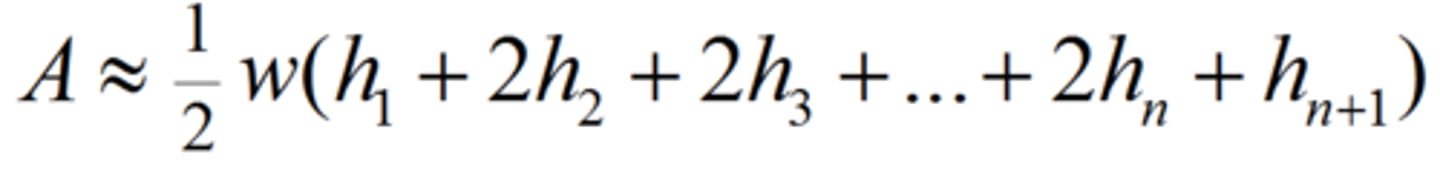
Simpson's Rule

Second Fundamental Theorem of Calculus

d/dx ∫ (from a to g(x)) f(t)dt= f(g(x))*g'(x)

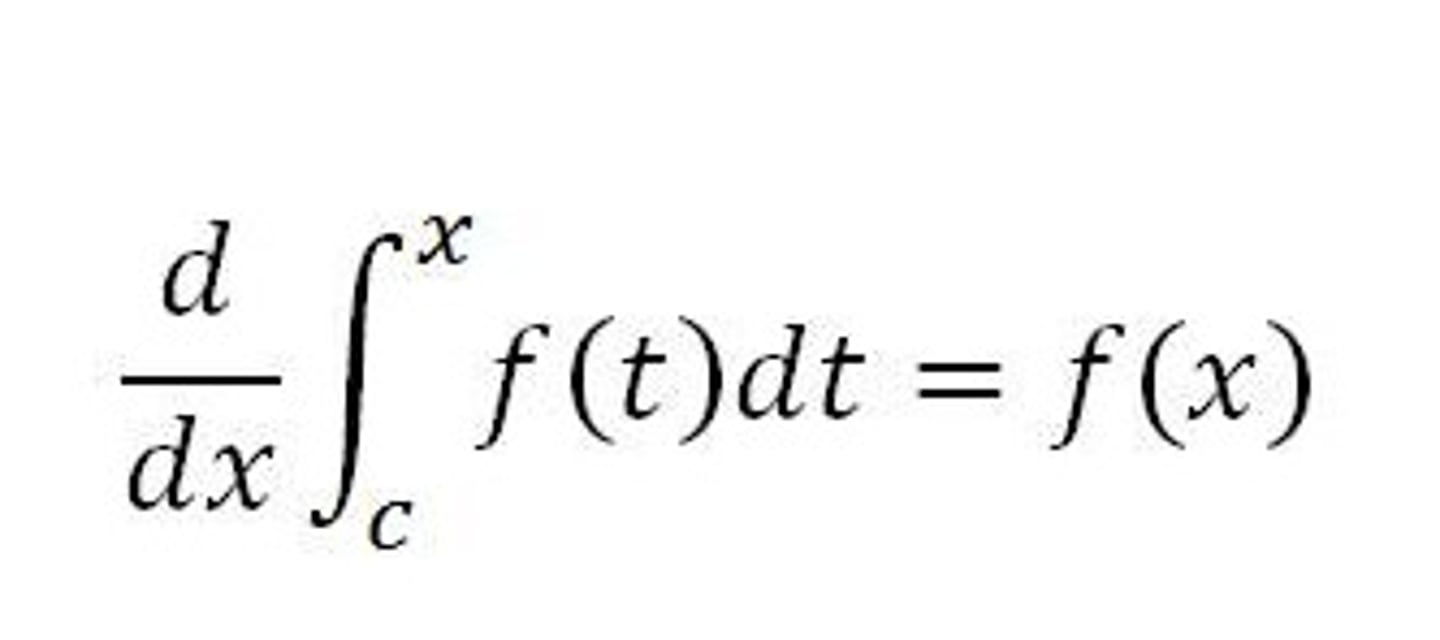
Fundamental Theorem of Calculus

∫ f(x) dx on interval a to b = F(b) - F(a)

Extension of Second Fundamental Theorem of Calculus

d/dx (b(x) ∫ a(x) f(t) dt) = f(b(x))b'(x) - f(a(x))a'(x)

Mean Value Theorem

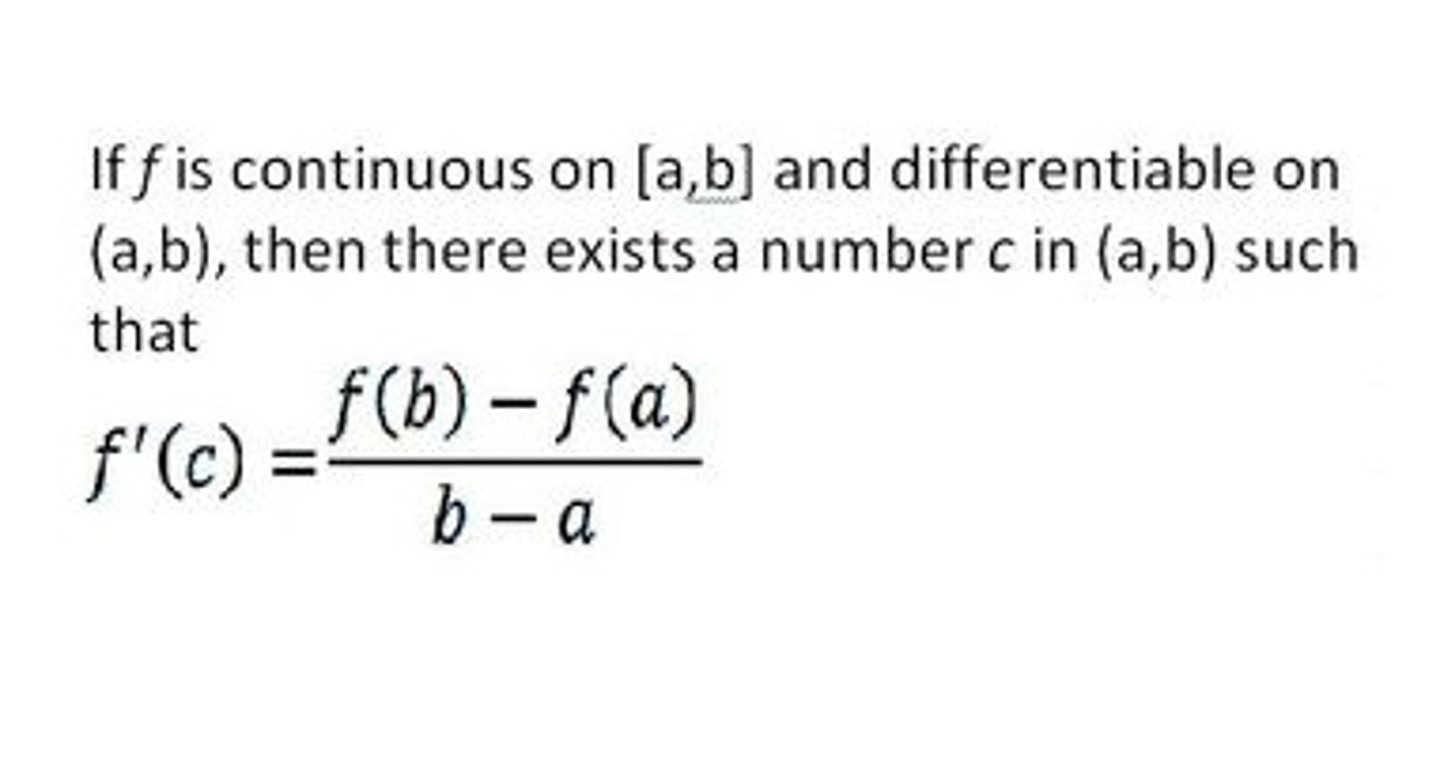
x^n antiderivative

x^n+1/n+1

sin(ax) antiderivative

-(1/a)cosx

cos(x) antiderivative

(1/a)sinx

csc(ax)cot(ax) antiderivative

-(1/a)csc(ax)

sec(ax)tan(ax) antiderivative

(1/a)sec(ax)

sec^2(ax) antiderivative

(1/a)tan(ax)

csc^2(ax) antiderivative

-(1/a)cot(ax)

b^ax antiderivative

1/(alnb)b^ax

1/(1 + (ax)^2) antiderivative

1/a(arctan)(ax)

1/sqrt(1 - (ax)^2)) antiderivative

1/a(arcsin)(ax)

tan(u) antiderivative

ln|sec u|

sec(u) antiderivative

ln|sec u + tan u|

cot(u) antiderivative

ln|sin u|

csc(u) antiderivative

-ln|csc u + cot u|

What is the Power Rule for derivatives?

dx(x^n) = n·x^(n-1)

What is the Constant Rule for derivatives?

dx(c) = 0

What is the Constant Multiple Rule for derivatives?

dx(c·f(x)) = c·f'(x)

What is the Sum Rule for derivatives?

dx(f(x) + g(x)) = f'(x) + g'(x)

What is the Difference Rule for derivatives?

dx(f(x) - g(x)) = f'(x) - g'(x)

What is the Product Rule for derivatives?

dx(f(x)·g(x)) = f'(x)·g(x) + f(x)·g'(x)

What is the Quotient Rule for derivatives?

dx(f(x)/g(x)) = [f'(x)·g(x) - f(x)·g'(x)] / [g(x)]^2

What is the Chain Rule for derivatives?

dx(f(g(x))) = f'(g(x))·g'(x)

What is the derivative of e^x?

dx(e^x) = e^x

What is the derivative of a^x?

dx(a^x) = a^x·ln(a)

What is the derivative of ln(x)?

dx(ln(x)) = 1/x

What is the derivative of log_a(x)?

dx(log_a(x)) = 1 / [x·ln(a)]

What is the derivative of sin(x)?

dx(sin(x)) = cos(x)

What is the derivative of cos(x)?

dx(cos(x)) = -sin(x)

What is the derivative of tan(x)?

dx(tan(x)) = sec^2(x)

What is the derivative of csc(x)?

dx(csc(x)) = -csc(x)·cot(x)

What is the derivative of sec(x)?

dx(sec(x)) = sec(x)·tan(x)

What is the derivative of cot(x)?

dx(cot(x)) = -csc^2(x)

What is the derivative of arcsin(x)?

dx(arcsin(x)) = 1 / sqrt(1 - x^2)

What is the derivative of arccos(x)?

dx(arccos(x)) = -1 / sqrt(1 - x^2)

What is the derivative of arctan(x)?

dx(arctan(x)) = 1 / (1 + x^2)

Integrating by parts

.

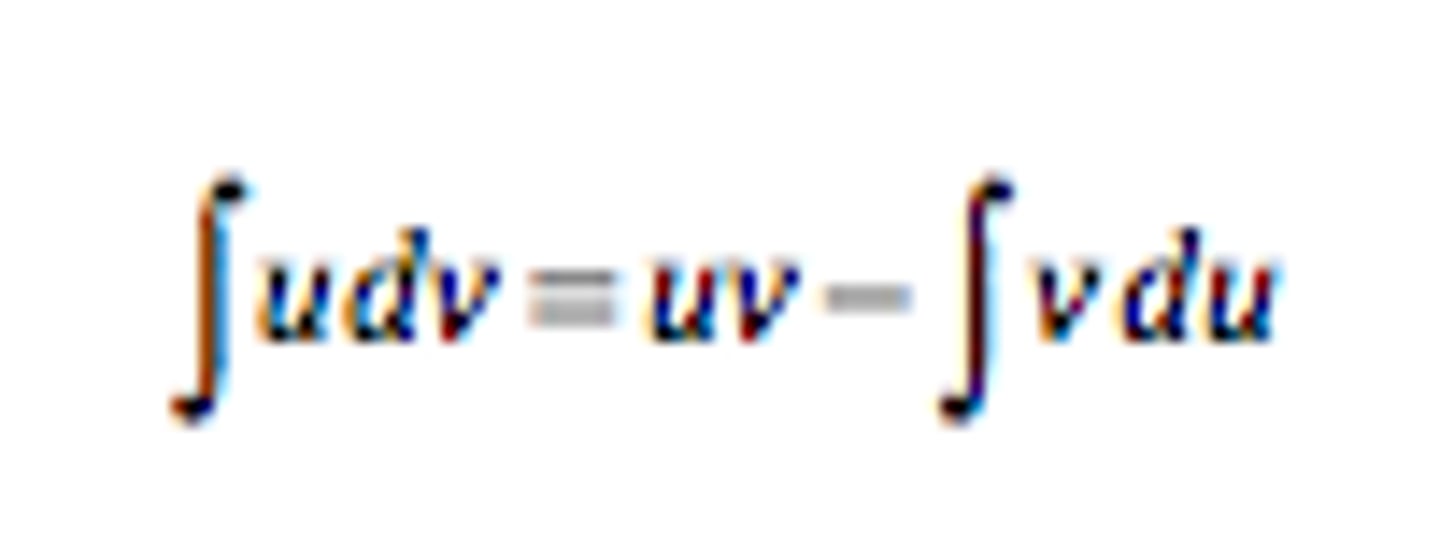
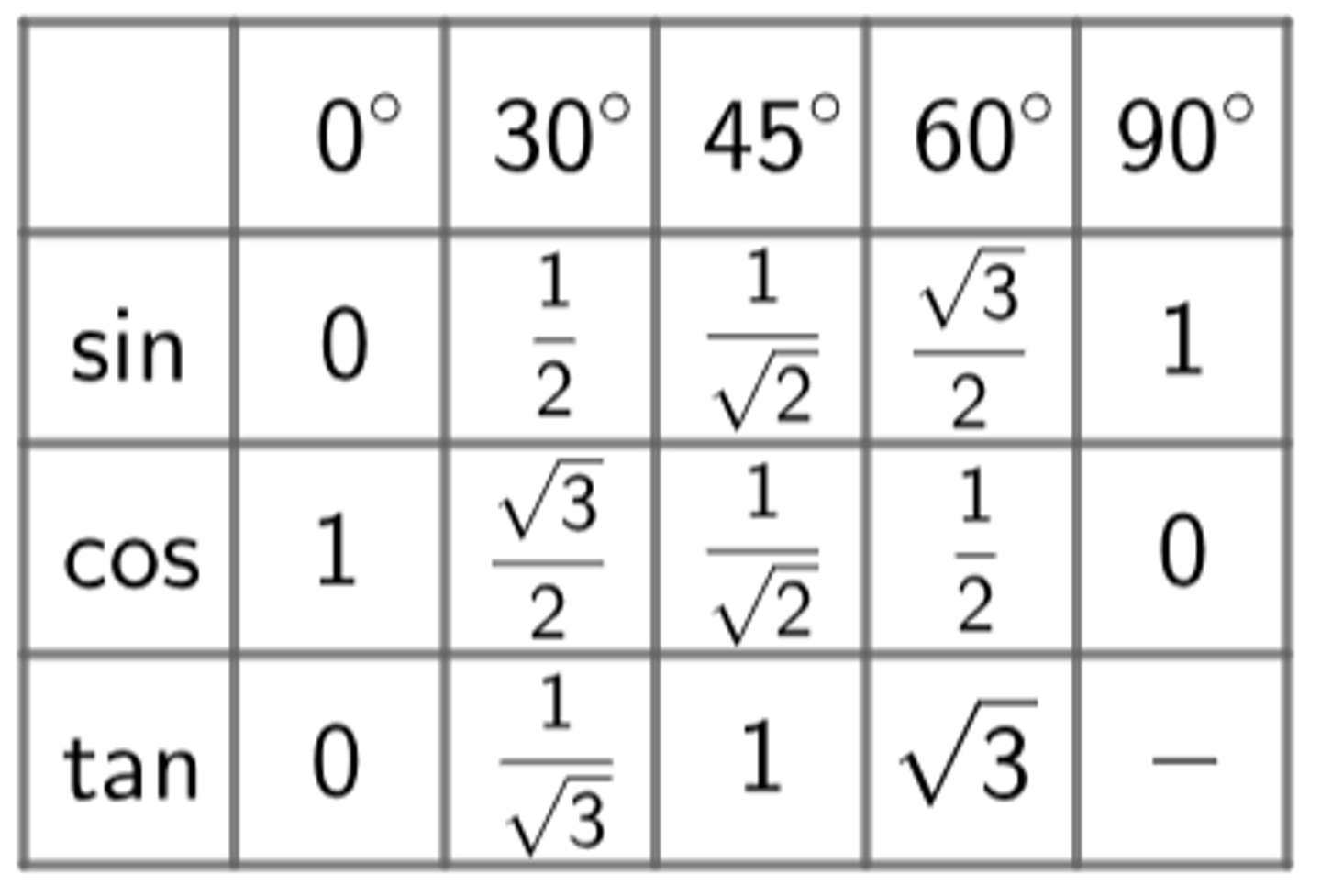
Sin/Cos/Tan Values

Trigonometric Identities

Sinθ/Cosθ = Tanθ

Cosθ/Sinθ = Cotθ

Cos²θ + Sin²θ = 1

Sinθ = Cos(90 - θ)

Cosθ = Sin(90 - θ)