Chem Ch 6

Microwave Radiation

Molecular rotational levels

Infrared radiation

molecular vibrational levels

Ultraviolet-visible radiation

electronic energy levels

What are the problems with wave theory

• Emission of light from hot objects

• The photoelectric effect

• Emission spectra

What is the Photoelectric Effect

Phenomenon where light shining on a metal surface ejects electrons from the metal

• Evidence for the particle nature of light

• threshold frequency must be reached

  • Below this, no electrons are ejected

  • Above this, the # of electrons ejected depends on the intensity of the light

Spectra tube

Emits light unique to the element in it

• Only a few wavelengths are seen

• Black regions are wavelengths that are absent

3 Postulates for Bohr’s theory of the atom

1. Electrons move in orbits that have defined energies

2. An electron in an orbit has a specific energy

3. Energy is only emitted or absorbed by an electron as it changes from one allowed energy state to another

Limitation of the Bohr Model

• Only explain the line spectrum of hydrogen

• Electrons are not completely described as small particles

• Doesn’t account for the wave properties of electrons

deBroglie equation

wavelength = Planck constant/mass*velocity

suggested that an electron moving about the nucleus of an atom behaves like a wave and therefore has a wavelength

Heisenberg’s Uncertainty Principle

We can’t determine the exact position, direction of motion, and momentum of an electron simultaneously

Erwin Schrodinger

Proposed an equation that contains both wave and particle terms

• Solving the equation leads to wave functions (shape of the electron orbital)

Orbitals

regions of highly probable electron locations

What 3 quantum numbers does Shrodinger’s equation require?

1. Principal Quantum Number: n

2. Azimuthal Quantum Number: l

   • l = n - 1

   • use letters s, p, d, and f for l

3. Magnetic Quantum Number: m_l

   • Dependent on l, values between -l to +l

s-Orbitals

• Spherical

• As n increases, the s-orbitals get larger

p-Orbitals

• three p-orbitals: px, py, and pz

• Correspond to allowed values of m_l of -1, -, and +1

• Orbitals are dumbbell shaped

• As n increases, p-orbitals get larger

Orbitals and their energies

• Orbitals of the same energy are said to be degenerate

• For n ≥ 2, the s- and p-orbitals are no longer degenerate because the electrons interact with each other

  • Therefore, the Aufbau diagram looks slightly different for many-electron systems

Pauli’s Exclusion Principle

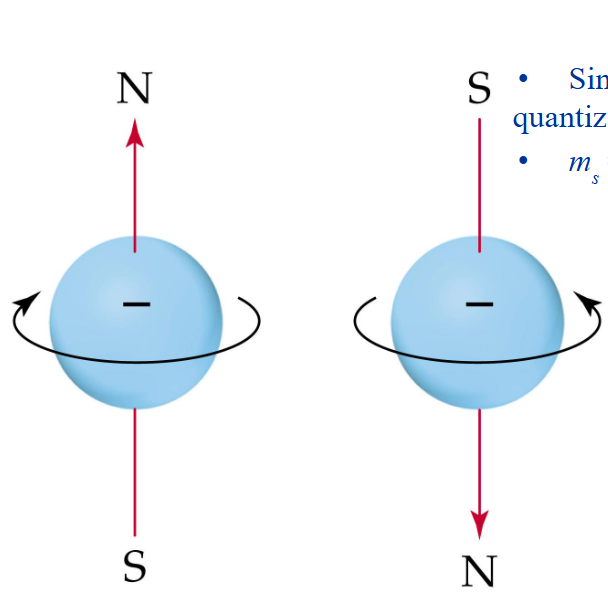
• Since electron spin is also quantized, we define

•  m_s = spin quantum # = ± ½

no two electrons can have the same set of 4 quantum numbers

• Therefore, two electrons in the same orbital must have opposite spins

• Electron capacity of sublevel = 4l + 2

• Electron capacity of energy level = 2n²

Hund’s Rule

for degenerate orbitals, electrons fill each orbital before any orbitals get a second electron

degenerate Orbitals

Orbitals of the same energy

paramagnetic atom

one or more unpaired electrons

• paramagnets do not retain magnetization in the absence of a magnetic field, this is because thermal energy randomizes electron spin orientations

diamagnetic atom

all electrons are paired

• repel magnetic fields

• unpaired electrons of paramagnetic atoms realign in response to external magnetic fields and are therefore attracted

Electron config notation

energy level, subshell, # of electrons per orbital

Orbital notation

each m_l value is represented by a line, electrons are also shown

Noble gas configuration/ “condensed config”

[Preceding noble gas] electron config notation for outer shell electrons

• valence electrons