STATS Test 2

Describing Quantitative Data

Finding the “center”

measures of central tendency show where the “center” of the data point lies

The Central Value

May or may not be a typical or frequent value in the data set

The common measures in a data set

1. Mean

2. Median

3. Mode

Mean Definition

1. the sum of the values divided by the number of values

2. if the data is from a sample the mean is shown as x bar

3. if the data is from a population the mean is shown as mew

X Bar

If you are working with a sample

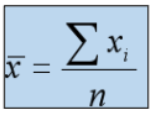
Mew

If you are working with a population

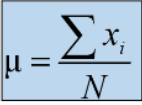
Calculating the mean

1. Add up everything (ex. the ages of all the supreme court justices)

2. Divide the sum by the amount there are (ex. how many ages are there to count up?)

3. sum over the number for the mean = #

4. interpretation: if (ex. age) were divided evenly among (ex. 9) judges, each would be (ex. 67.8) years old.

Median Definition

The median identifies the data set center by establishing a value such that at least half the numbers in the data set are at or above that value and at least half the numbers are at or below that value

Median Facts

1. the median is the middle value in an ordered list of the data (order it from smallest to largest)

2. when data has extreme values, the median is usually preferred to find a central location. it is less affected by extremes than the mean.

3. if there are an even number of its, the median is the value of the middle item (n+1)/2 in an order

4. if there are an even number of its, the median is the value of the average between the two middle items. (n/2) and (n/2)+1 in an order

Calculating the Median

Ex.

1. Order the list from smallest to largest

2. There are 9 values

3. so (n+1)/2 is (9+1)/2 which is 5

4. the median is the 5th value in the ordered list

5. the median, in this case, is 65 (don’t forget the unit. in this case, years)

6. Interpretation: at least half of the justices are 65 years old or older and at least half are 65 years old or younger

Mode Definition

1. The mode of a data is the most frequently occurring value

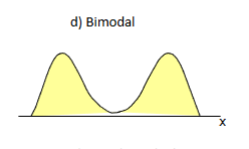
2. a data set can have zero/none, one (unimodal), two (bimodal), or more (multimodal) modes

Measures of Dispersion Definition

Measures of dispersion tell us how much variation or dispersion there is in the data around the central value. in other words, how spread out are the data points?

Common Measures of Dispersion

1. Range

2. mean absolute deviation (MAD)

3. Variance

4. Standard Deviation

Range Definition

1. the difference between the smallest and the largest values in the data set

2. the simplest measure of variability

3. very sensitive to the smallest and largest data values

Range Example

1. Order from smallest to largest

2. Largest number - smallest number = range (units)

3. Interpretation: There is a (#) difference between the (ex. oldest and youngest justices)

Mean Absolute Deviation (MAD) Definition

1. The MAD measures the average absolute distance (or deviation) of values in the data set from the data set mean

2. if the data set is a population or sample it changes the equation slightly between X bar and Mew

Mean Absolute Deviation (MAD) Types

1. If the data is a sample

2. if the data is a population

Mean Absolute Deviation (MAD) Sample

X Bar

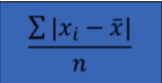
Mean Absolute Deviation (MAD) Population

Mew

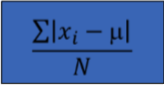
Mean Absolute Deviation (MAD) Example

1. organize the data in smallest to largest order

2. have the mean

3. Study the equation

Variance Definition

1. The variance is the average of the squared differences between each data value and the mean

2. if the data set is the sample, the variance is denoted by s²

3. If the data set is a population the variance is denoted by o²

Variance Sample

s²= image

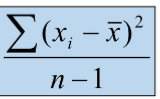
Variance Population

O²=Image

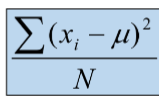
Distribution of Shape

1. symmetric

2. bimodal

3. positively skewed

4. steeply peaked

5. negatively skewed

6. flat

Distribution of Shape: Symmetric

cut in half it would look the same

Distribution of Shape: Bimodal

2 humps

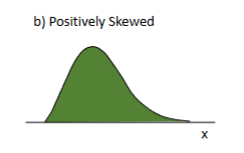
Distribution of Shape: Positively Skewed

skewed right?

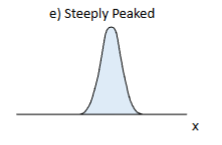
Distribution of Shape: Steeply Peaked

One giant peak and not much (if anything) on the sides

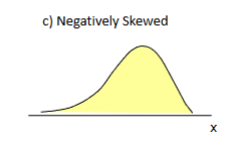
Distribution of Shape: Negativly skewed

Skewed Left

Distribution of Shape: Flat

A flat graph like a box or rectangle.

Standard Deviation Definition

1. The standard deviation of a data set is the positive square root of the variance

2. it is measured ion the same units as the data, making it more easily interpreted than the variance.

Standard Deviation Formula Sample

1. if the data set is a sample, the standard deviation is denoted by s= image

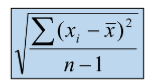
Standard Deviation Formula Sample

1. if the data set is a population the Standard Deviation is denoted by o = Image

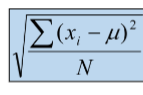
Distribution Shapes (Vocab)

1. Symmetric

2. Skewness

3. Kurtosis

Symmetric Definition

Can split the distribution into two identical halves

Skewness Definition

An asymmetry in which an elongated tail extends in either the right-hand direction (positive skewness) or the left hand direction (negative skewness)

Kurtosis Definition

The degree of peakedness or steepness in a distribution

The Effect of Distribution Shape on Descriptive Measures

1. the shape of the distribution influences nearly every summary measure

2. when distribution is perfectly symmetrical, the mean and median values are the same

3. when distribution is skewed this equivalence disappears. this is when the median is more representative of the data set than the mean.

4. extreme values affected most of the common measures of disposition

5. the range is radically affected by a single extreme value

6. this is also true to a lesser extent of the variance and standard deviation. the MAD is somewhat less susceptible.

Distribution Shape: Frequency Distributions Definition

1. When the data set has a small number of possible values that occur with some frequency, a frequency distribution can reveal the distribution shape.

Building a Frequency Distribution

1. A frequency distribution is a tabular summary of a set of data showing the frequency (or number) of items in each of sever nonoverlapping classes

2. the objective is to provide insights about the data that cannot be quickly obtained by looking only at the original “raw“ data

3. for each qualitative data, this means simply counting the number of times each value occurs

4. for quantitative data, this means either counting values for variables that take a small number of discrete values or grouping the values for variables that take many values over a continuous range.

Distribution Shape: Bar Chart

1. A bar chart is a graphical device for depicting qualitative or quantitative data that have been summarizing in a frequency, relative frequency, or cumulative frequency distribution

2. on the horizontal axis, specify the tables/values that are used for each of the classes/values

3. a frequency, relative frequency, or cumulative frequency scale (but only one) can be used for the vertical axis

4. using a bar or fixed width drawn above each class label/value, we extend the height appropriately

5. the bars are separated to emphasize the fact that each class/value is a sperate category/discreet value

Distribution Shape: Group Data

1. when the data takes a large number of values, and few (if any) observations have the same value, the observation need to be grouped in order to see the distribution shape

Grouping the Data Guidelines

1. classes should touch but nit overlap

2. classes should be of equal width

3. open ended classes should be avoided

4. the number of classes should be close to the smallest value of k for which 2^k > n or N

5. the upper and lower boundaries for each class -the class limits, but be set in a way that makes them readable and intuitive (ex. chooses 1 to 4.99 not 1.13 to 5.13)

6. approximate class width: largest value - smallest value /divided by number of classes

Histograms Definition

1. another common graphical presentation of quantitative data is a histogram.

2. the variable of interest is placed on the horizontal axis and the frequency or relative frequency (only 1) is placed on the vertical axis

3. a rectangle is drawn above each class interval with its height corresponding to the interval’s frequency or relative frequency (use only 1)

4. unlike a bar graph, a histogram has no natural separation between rectangles of adjacent classes.

Approximating Descriptive Measures

1. Therse measures can be used to obtain approximations of the mean, variance, and standard deviation for the frequency distribution of grouped data

2. to compute the weighted mean, treat the midpoint of each interval (m_i) as a representative value for all of the group (or class) members

3. compute the weighted average of the class midpoints using the class frequencies as weights (f_i)

4. similarly, in computing the variance and standard deviation, the class frequencies are used as weights.

5. for a relative frequency distribution, substitute the relative frequencies p_i for f_i in the formulas and do not divide by N