Unit 2 - Calculus and Physics

What is a Limit?

How is it read?

A limit allows us to evaluate the output (typically a limit) of a func at a certain x value

lim / x —> c f(x) = L is read as “as x approaches the value c, the func f(x) will approach L (the limit)“

What MUST you do when determining a limit and why?

you MUST ALWAYS FACTOR the function given in a limit.

• The magic of the limit is by factoring the function

• If we do not, we will get a undefined result 

EX: if we plug 3 into x² - 9 / x - 3 we get 0/0 or undef

• If we factor it into (x-3)(x+3)/ (x-3) we get x+3 and now we get 6.

What is a Derivative and what does it give?

What is it VERY useful for? (rate of change)

A Derivative is a function that gives us the slope of the tangent line to the OG func

—> slope of tangent line at x=c means derivative of f(x) at x=c

• A Derivative is very useful to find the rate of change in smth

What are the 2 ways to get the slope of the tangent line of a graph?

What does this tell us?

we will use the graph of f(x) = x³ and the point x = 2

1. Limits (stinky)

   • we need to create a limit expression and factor it so (y₂ - y₁)/ (x₂ - x₁) which is f(x) - f(2)/ x - 2 and we can factor it to x² + 2x + 4 = 12

2. Derivatives

   • we will take x³ and use the power rule to make it 3x² and put in 2 = 12

basically Derivatives let us find the tangent line to the OG func using the limits of secant lines (approaching x=2)

What are the 4 ways you can write the derivative of f(x) at x = c?

1. f’ (c)

2. M_tan = lim x—>c (M_sec)

3. lim x —> c f(x) - f(c)/ x-c

What is the equation definition for a derivative?

What happens to x-c as x gets closer to c?

look at photo

What is lebnitz notation?

How can f’ (c) be written?

Lebnitz’s notation is dy/dx (“the derivative of y with respect to x“)

• f’ (c) can be written as dy/dx | x = c

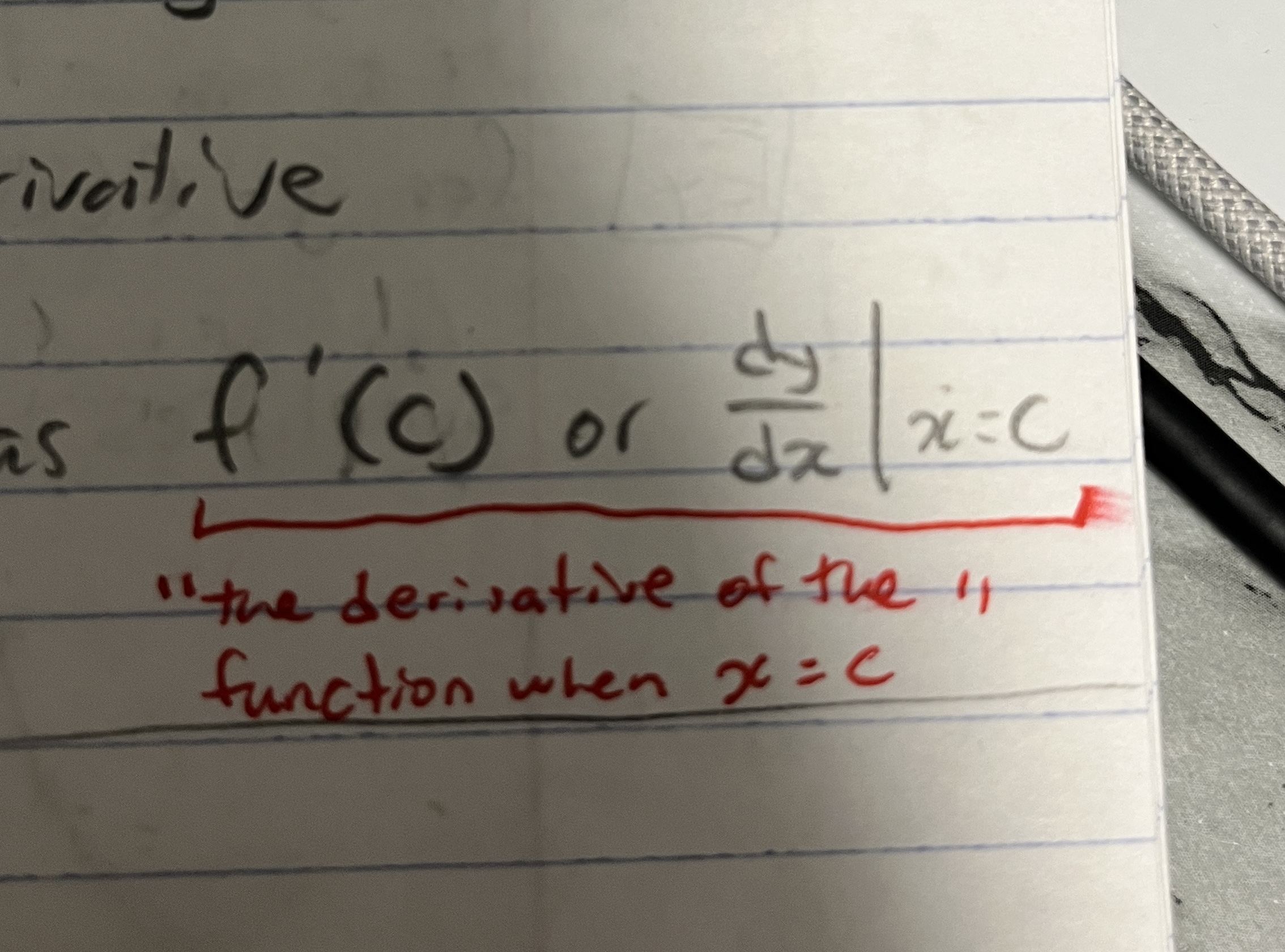
In Physics, what will a secant line and a tangent line find?

secant = avg ____

tangent = instantaneous ______

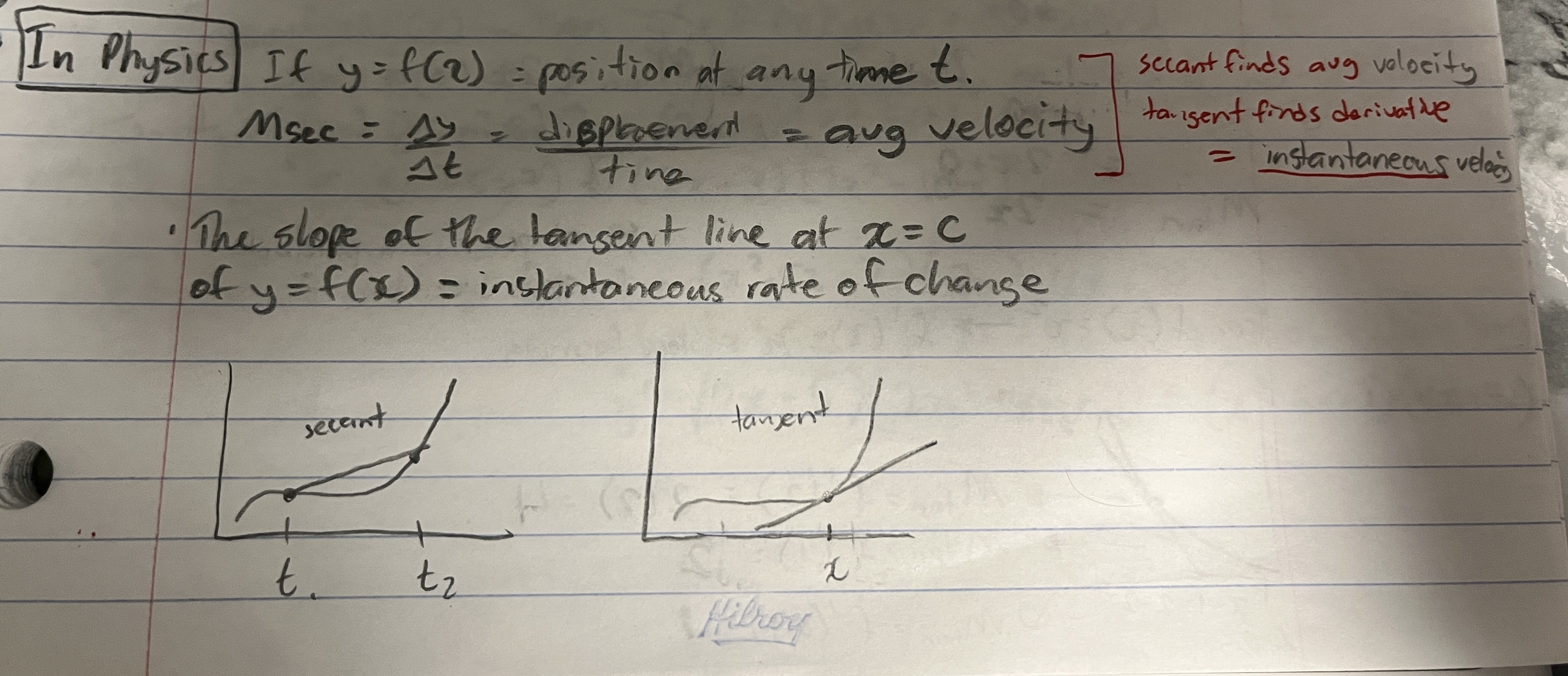
What should you do when a Q asks for the derivative of a physics term?

Imagine a graph of that term over time and remember the slope.

EX: Derivative of position = velocity (cus velocity is the slope of a dt graph)

What are the 6 Derivative Rules?

(very important to know!)

1. The Derivative of a constant (horizontal line) is 0

2. If y= f(x) = mx+b, then derivative = m (cus linear slope)

3. Power rule: f’(x)= nx^(n-1)

4. If y = af(x) + bg(x), y’ = af’(x) + bg’(x)

5. Product Rule: if y = f(x)g(x), then y’= f’(x)g(x) + g’(x)f(x)

6. Chain Rule: if y = f(g(x)), then y’ = f’(g(x)) x g’(x)

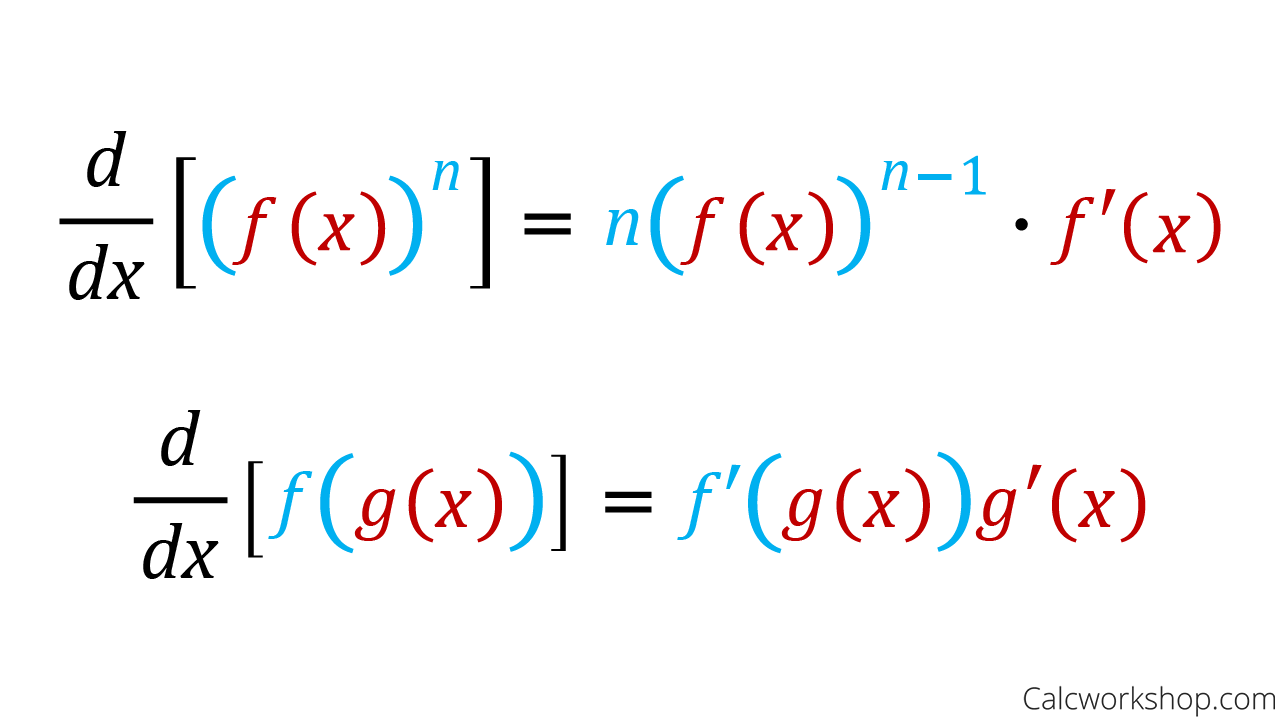
Based on sm Theorem, where are the Maximum and Minimum points on a function that has been differentiated?

—> What does this mean for Physics Qs?

• The Max/min points will show on either ends of a given interval as well as the point where the derivative = 0

—> This means in a Physics Q asking for max/min velocities within a given interval, we test the lowest, highest and point that makes derivative 0.

|

EX: particle moving at v(t)= t³ - 27t + 60. What is min/max speeds in the interval 0 <= t <= 5s?

1. V’(t) = 3t² - 27 —> t = +-3

2. reject -3 cus outside of interval

3. we must test t = 0 = 60m/s, t = 5 = 50 m/s and t = 3 = 6 m/s

4. max = 60 m/s and min = 6 m/s

What is a 2nd derivative?

What is acceleration a 2nd derivative of pos/disp?

The 2nd derivative is the derivative of a derivative. 

• It tells us the curvature/concavity of the function’s graph

Acceleration is a 2nd derivative of position/displacemet cus its the slope of the slope (accel is the slope of velocity)

if accel > 0, then position graph will CURVE up (velocity will be linear rise )

if accel < 0 then pos graph will Curve down

What does the 2nd derivative > 0 or <0 tell us?

• if f’’(x) > 0, then graph will be concave (curved) up with the tangent line below the graph.

• if f’’(x) < 0, then graph will be concave (curved) down with the tangent line above the graph.