QP Unit 2.7 Osmosis and Osmotic Pressure

Define osmosis and osmotic pressure

Osmosis is the movement of fluid across a membrane in response to differing concentrations of solute on the two sides of the membrane. Osmotic pressure is the pressure necessary to stop osmotic flow across a barrier that is impermeable to the solute. Osmosis is only defined for semipermeable membranes, which are impermeable to solute but permeable to water.

Write van’t Hoff’s limiting law for osmotic pressure dependent on concentration

The van’t Hoff equation relates osmotic pressure to concentration where R is the gas constant (0.082 L atm mol^-1 K^-1), T is absolute temperature, and C is molar concentration of solute in the inner compartment. In a mixture, osmotic pressures due to each solute particle add up.

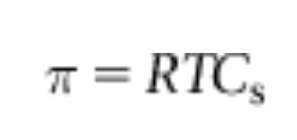
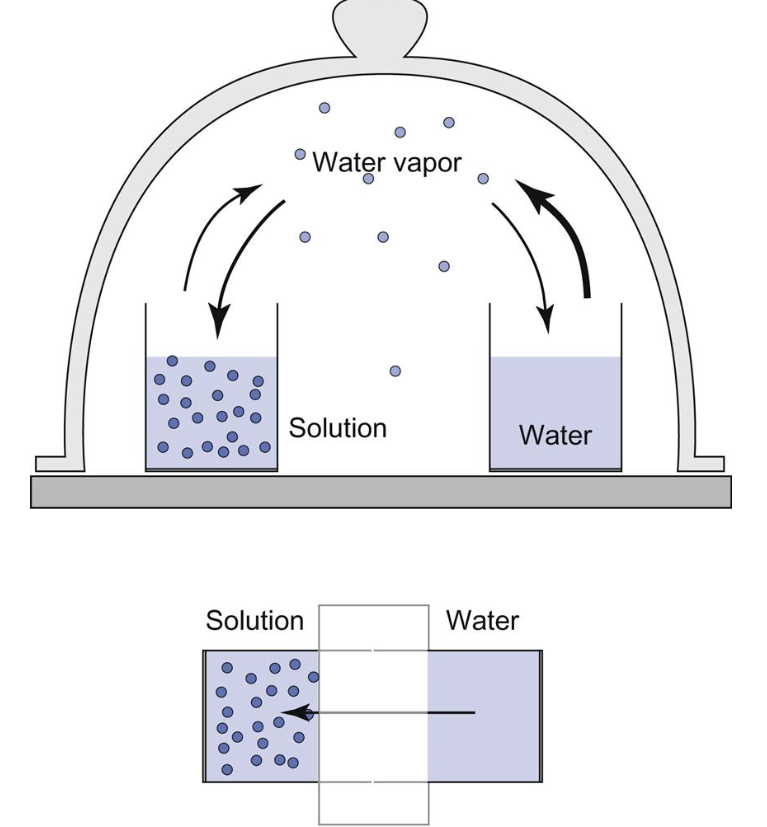
List the colligative properties of solutions and explain why vapor pressure depression perfectly predicts osmotic pressure

The colligative properties are freezing point depression, boiling point elevation, and vapor pressure depression which are all caused by dissolving solutes in a solution. Osmosis pressure and vapor pressure depression are perfect predictors of each other because essentially they are the same phenomenon.

Describe the osmotic coefficient for correction of nonideality in solutions

Osmotic coefficient phi is equal to observed osmotic pressure divided by (RTCs). This value can be less than or greater than 1.

Be able to calculate predicted osmotic pressure for a solution

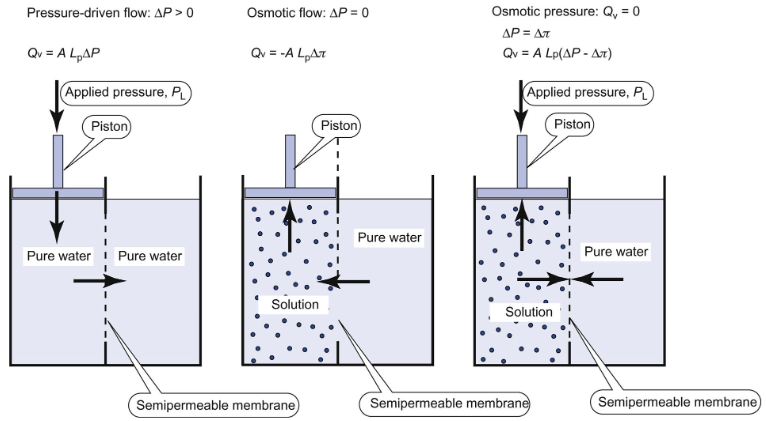
Define hydraulic conductivity or hydraulic permeability

Constant Lp, flow is linearly related to presure difference by the area of the membrane (A) and proportionality constant, Lp, that is characteristic of the membrane. Flpow is linearly related to difference in osmotic pressure, delta pi, by the area of the membrane and the hydraulic conductivity.

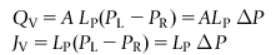
Define the reflection coefficient

When membranes are partially permeable to the solute (leaky membranes), measured osmotic pressure is less than that predicted by van’t Hoff Law. Sigma, the reflection coefficient can be seen in the equation attached, where pi eff is the observed osmotic pressure and phi RTC is the theoretical osmotic pressure that would be observed if the membrane was perfectly semipermeable. This value ranges from 0 to 1.

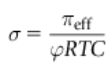
Explain how the hydraulic conductivity depends on the microscopic parameters of the membrane

• Case 1: Solute is very small compared to the pore

  No contribution to osmotic pressure, delta s=0.

• Case 2: Solute is much larger than pore

  Membrane is impermeable to solute, sigma s=1.

• Case 3: Solute is slightly smaller than pore

  Partial exclusion from the pore 0<sigma s<1

Write an equation for volume flow across a microporous membrane in the presence of hydraulic and osmotic pressures

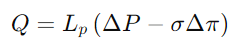
Describe the origin of the osmotic pressure for microporous membranes

The osmotic pressure for microporous membranes arises from the difference in concentration of solute particles across the membrane. When a solute is present on one side of a microporous membrane and absent on the other, water moves toward the higher solute concentration to balance the solute levels. This movement of water creates a pressure that can be measured as osmotic pressure. The size and nature of the pores in the membrane determine how effectively it can separate solute and solvent, influencing the observed osmotic pressure.

Describe how erythrocyte cell volume changes when placed in contact with solutions of varying [NaCl] or [glucose]

Hypertonic- solution causes cell to shrink, hypotonic- solution causes cell to swell, isotonic- causes neither shrinking nor swelling

Contrast the concepts of tonicity and osmolarity

Osmolarity is a property of a solution, but tonicity is not. Tonicity refers to the direction of osmotic flow when a particular solution is placed in contact with a particular cell. Tonicity involves real membranes rather than an ideal, semipermeable membrane. The real membrane has a set of reflection coefficients, one for each solute on each side of the membrane. Whether shrinking or swelling occurs depends on the osmotic concentrations and compositions of the two solutions on the two sides of the cell membrane, and on how these solutes interact with the real biological membrane.

Describe the behavior of a perfect osmometer

A cell acting as a perfect osmometer would exhibit a relationship where its volume decreases as the osmolarity of the external medium increases. This implies that as the concentration of solutes outside the cell rises, water moves out of the cell to the area of higher solute concentration, causing the cell to shrink. The relationship is expected to be linear, with a slope that indicates the sensitivity of cell volume to changes in external osmolarity and with an intercept of zero, meaning that at zero osmolarity, the cell would maintain its original volume.

Explain why cells are not perfect osmometers

Cells are not perfect osmometers because they have semi-permeable membranes that allow certain solutes to pass through while excluding others. Additionally, biological membranes have various reflection coefficients for different solutes, leading to discrepancies between the osmotic behaviors of cells and those predicted by ideal osmometry. Other factors such as active transport mechanisms, cell rigidity, and cellular metabolism can also impact how cells respond to changes in osmotic pressure.

Define RVD and RVI

RVD (regulatory volume decrease) is when a cell that initially swells when placed in hypertonic medium may eventually lose some of its acquired volume. The swelling of the cell activates compensatory mechanisms that cause transport of osmotically actice solutes (osmolytes) out of the cell.

RVI (regulatory volume increase) is when cell shrinking activates an influx of osmolytes leading to a compensatory swelling.