Orbital Mechanics 2

Orbit Changes

• “… figuring how to go from one orbit to another…”

• “… assume that the initial and final orbits are in the same plane.”

• “… manoeuvres to move spacecraft from their initial parking orbits to their final mission orbits “

Fuel Efficient (Elliptical) Orbit Transfer → Hohmann Transfer

How can a spacecraft change its energy ?

→ By increasing or decreasing its velocity (velocity change ΔV) with thrusters/engines

• ΔV is tangent to initial and final orbits

• These tangential ΔVs are the real secret to the Hohmann Transfer’s energy savings

Specific Orbital Energy

\epsilon=-\frac{\mu}{2a}

Cases:

IF, we want to move a spacecraft to a higher orbit, we have to increase the semimajor axis (adding energy to the orbit) by increasing velocity.

On the other hand, to move the spacecraft to a lower orbit, we decrease the semimajor axis (and the energy) by decreasing the velocity.

Ellipctical Orbit Velocity:

v=\sqrt{\mu\cdot\left(\frac{2}{r}-\frac{1}{a}\right)}

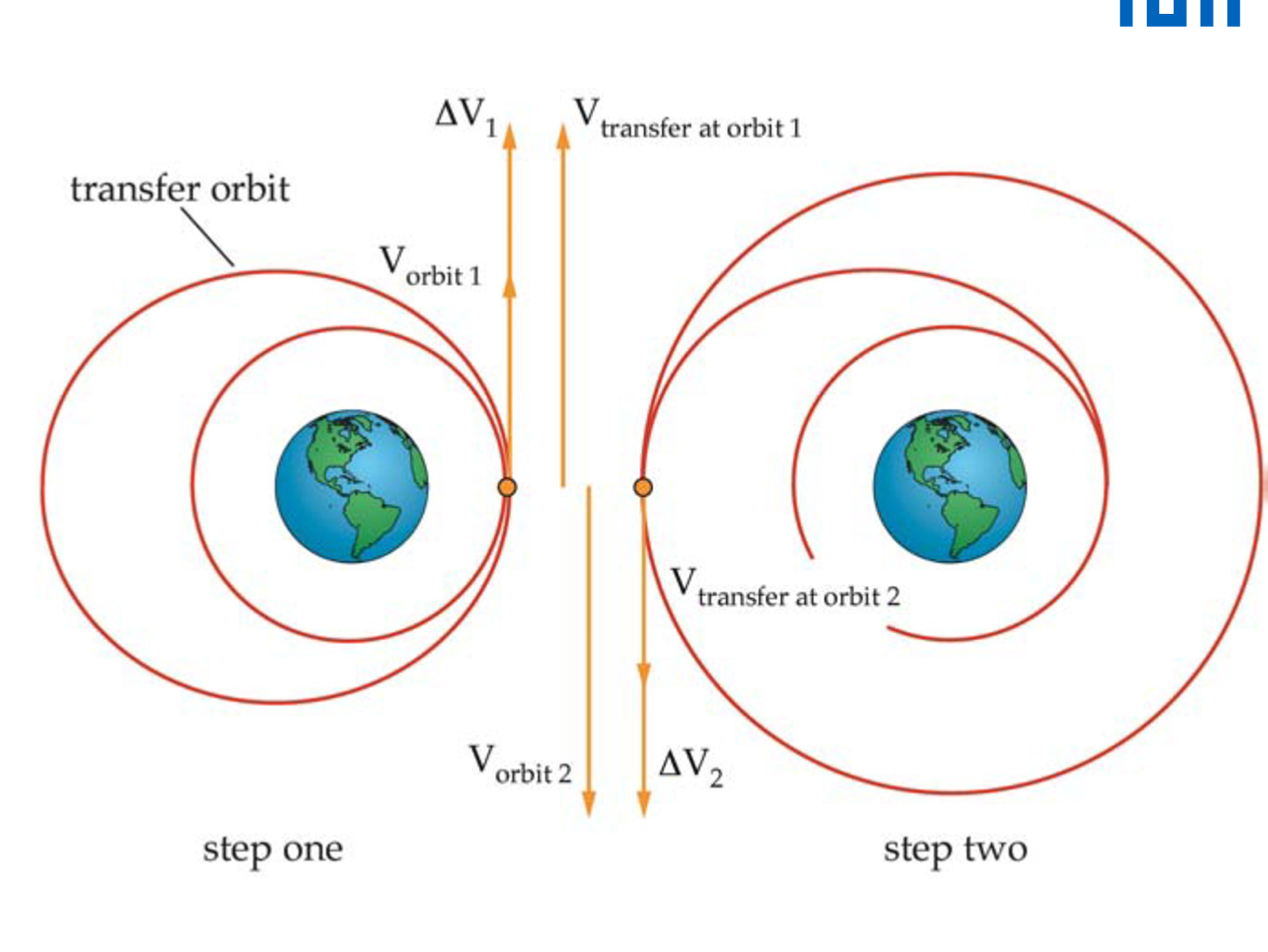
Hohmann Transfer (Steps)

Procedure:

1. First Burn (ΔV_1): Takes Spacecraft from initial, circular orbit to transfer, ellliptical orbit

2. Second Burn (ΔV_2): Takes Spacecraft from elliptical, transfer orbit to final, circular orbit

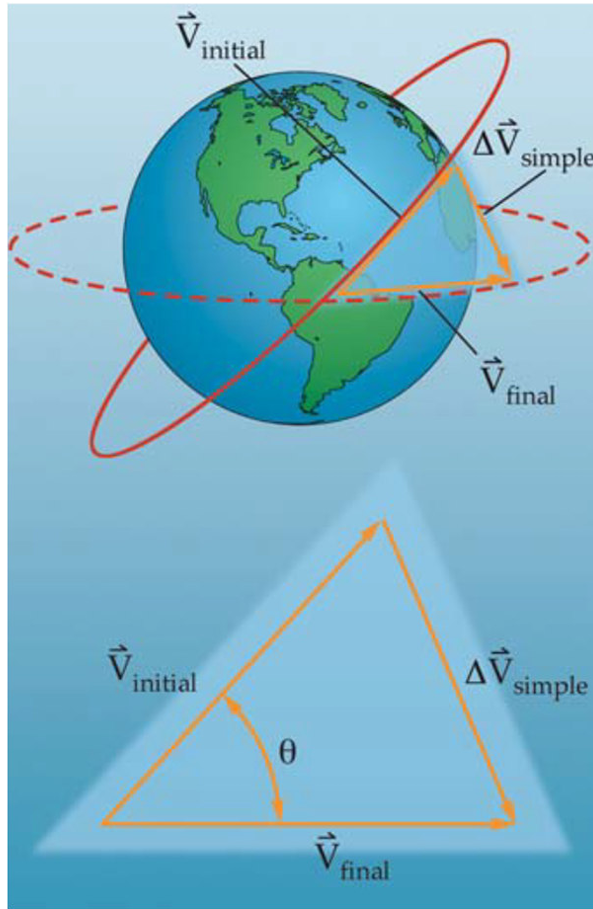
Plane Changes

→ rotate orbit plane by an angle θ; change direction of velocity vector in order to change orbit plane

Velocity change required for a simple plane change, i.e. rotate plane:

\Delta V_{simple}=2V_{Initial}\sin\left(\frac{\theta}{2}\right)

V_Initial = V_Final: Velocity in the initial and final orbits the same

θ = plane change angle (deg or rad)

Remark!

• Escape velocity same as required velocity change for 90deg. plane change

• \Delta V at ascending node or descending node → Changing only inclination of orbit

• Use Plane change to change right ascension of the ascending node, Ω (RAAN)

  • \Delta V  at North- or South Pole for polar orbits ( i = 90°)  → Performing  \Delta V  where intial and final orbits intersect → Changing only right ascension of the ascending node, Ω (RAAN)

• V_Initial directly influences  \Delta V , choosing point of plane change (either at apogee or perigee) in elliptical orbit has big impact in maginitude of \Delta V

Rendezvous

→ One spacecraft arrives/meets with another, second spacecraft/target in the same point/place at the same time

Co-planar Rendezvous

1. → Hohmann Transfer between co-planar orbits (two orbits in the same plane)

• angular velocity ω:

\omega=\frac{2\pi}{2\pi\sqrt{\frac{a_{}^3}{\mu}}}=\sqrt{\frac{\mu}{a^3}} ,

P=2\pi\sqrt{\frac{a^3}{\mu}}

• Time of Flight:

TOF=\pi\sqrt{\frac{a^3_{transfer}}{\mu}}

, for circular orbit: a = r (radius)

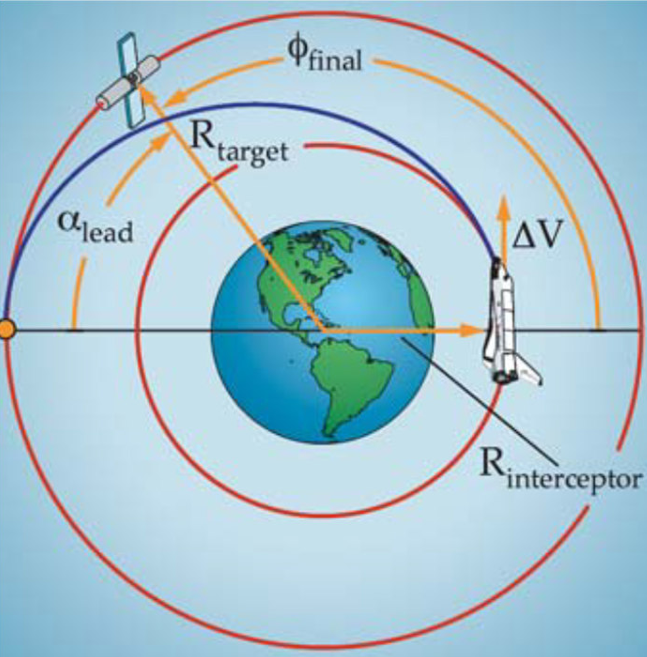
• Lead Angle α_lead:

\alpha_{lead}=\omega_{t\arg et}\cdot TOF

• Phase Angle/Head Start of Target φ_final:

\phi_{final}=\pi-\alpha_{lead}=\phi_{Initial}+\left(\omega_{t\arg et}-\omega_{Intercepor}\right)\cdot t_{wait}

• wait time t_wait:

t_{wait}=\frac{\left(\phi_{final}-\phi_{intial}\right)}{\left(\omega_{t\arg et}-\omega_{Interceptor}\right)}

Co-orbital Rendezvous

→ the target and interceptor are in the same orbit, with one ahead of the other, done by interceptor moving into into a waiting or phasing orbit that will return it to the same spot one orbit later in the time it takes for the target to move around to that same time

Two methods:

1. Slow Down to Speed Up: target ahead of interceptor in same orbit, interceptor slows down, entering smaller orbit with a shorter period.

2. Speed Up to Slow Down: target behind interceptor in same orbit, interceptor speeds up, entering higher, slower orbit

• How far target has to travel to reach interceptor’s current position φ_travel:

\phi_{travel}=2\pi-\phi_{initial}

• tim taken to cover this travel angle:

TOF_{t\arg et}=\frac{\phi_{travel}}{\omega_{t\arg et}}

\omega=\sqrt{\frac{\mu}{a_{t\arg et}^3}}

TOF_{pha\sin g}=\frac{2\pi}{\omega_{pha\sin g}}

→ Final Equation:

2\pi\cdot\sqrt{\frac{a_{pha\sin g}^3}{\mu}}=\frac{\phi_{travel}}{\omega_{t\arg et}}

Remark:

• Knowing size of orbit, able to compute necessary  \Delta V  for rendezvous

• First \Delta V_1 slows interceptor and put it into phasing orbit

• Second \Delta V_2  returns it to original orbit

• \Delta V  ‘s have the same magnitude 

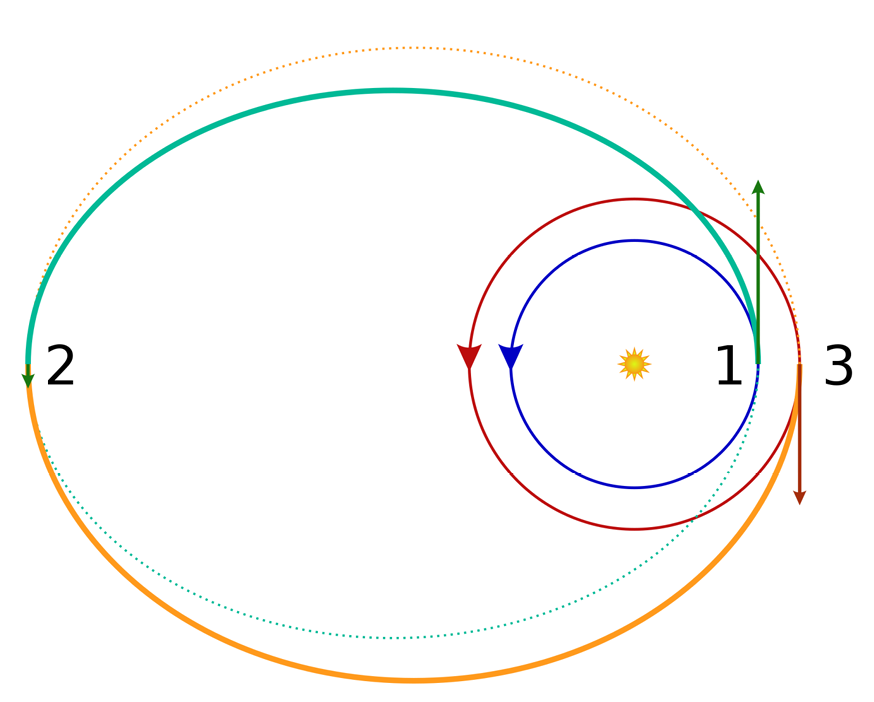
Bi-elliptic Transfer

→ Subsitute for Hohmann Orbit Transfer, sometimes more useful

→ Consists of two half-elliptical orbits

Procedure:

1. First Burn: Expends \Delta V_1 to boost spacecraft into first transfer orbit, with apoapsis/apogee at some point rb (2)

2. Second Burn: \Delta V_2 sends spacecraft into second elliptical orbit, with periapsis/perigee at the radius of the final desired orbit (3)

3. Third Burn: \Delta V_3 injects spacecraft into desired orbit

Compared to Hohmann Transfer…

• Require one more burn

• Generally require a greater travel time

Critical Threshold Value:

ratio of final to initial semi-major axis is 11.94 or greater

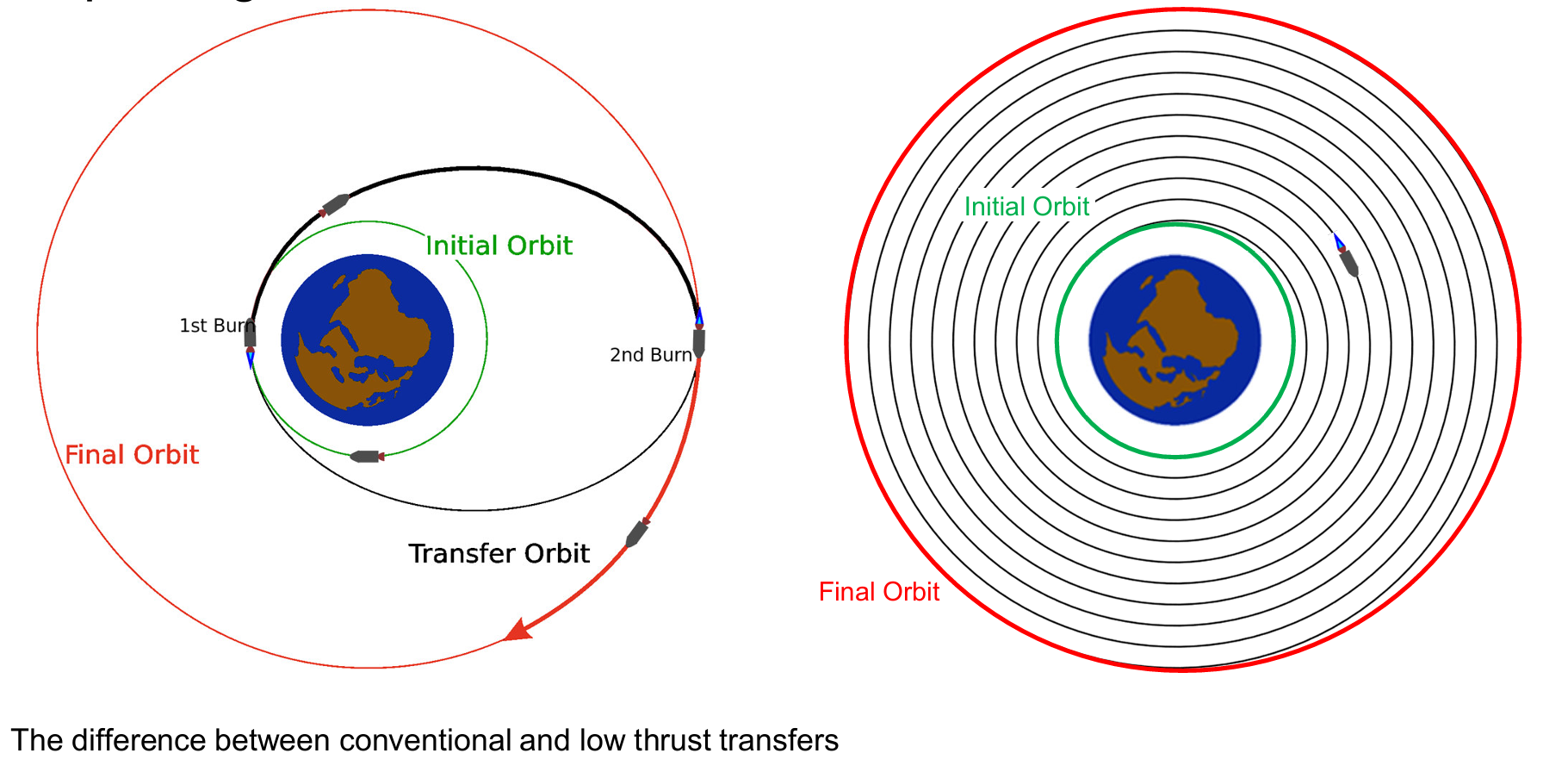
Spiraling

Different to Hohmann- and Bielliptic Transfer, continous small thrusting (w. electric propulsion system); larger travel time

Gravity Assist

→ Use of relative movement (e.g. orbit around the Sun) and gravity of a planet or other astronomical object to alter the path and speed of a spacecraft, typically to save propellant and reduce expense

• Orbit pumping: A gravity assist that changes the magnitude of a spacecraft’s velocity

• Orbit cranking: Using a planet’s gravity to change the direction of travel

e.g. Voyager 1 and 2

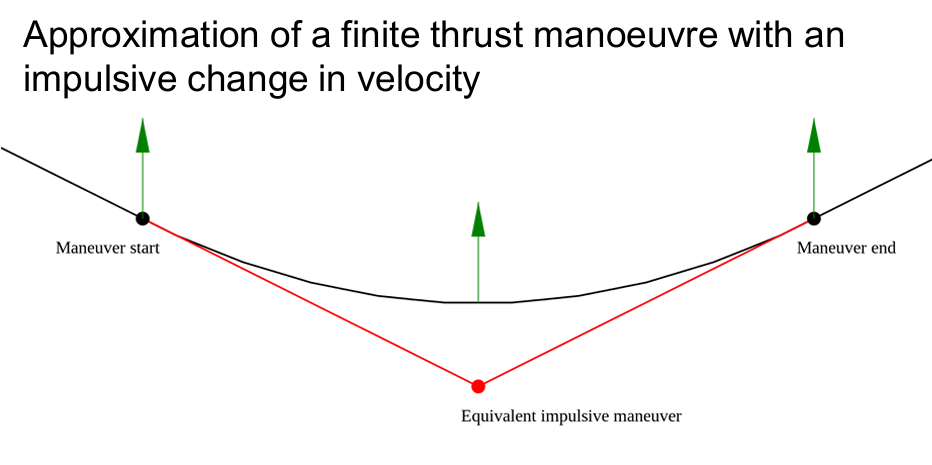
Impulsive vs Finite Manouevres

Impulsive Manouevre: instantaneous change in the spacecraft's velocity (magnitude and/or direction), limit case of burn to generate particular amount of thrust as burn time tends to zero

In physical real world not possible.

Entry/Re-entry

“Atmospheric entry is the movement of an object from outer space into and through the gases of an atmosphere of a planet, dwarf planet, or natural satellite”

Types:

• uncontrolled entry: entry of an astronomical object, debris (NO propellant)

• controlled entry/re-entry: navigated or predetermined course of entry; EDL = Technology or Procedure ensuring controlled entry,descent and landing of spacecraft

---

Entry/Re-entry → Atmospheric Drag & Compression of Air→ mechanical stress & aerodynamic heating

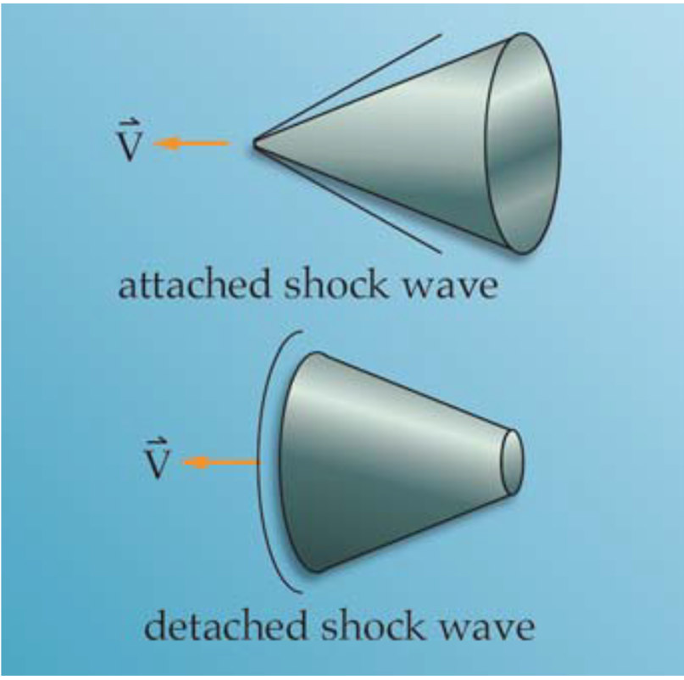
Entry/Re-entry → Compression of Air infront of object →  shockwave

Shockwave (shape, exposed area matters):

• Attached Shockwave: High BC → localized heating

• Detached Shockwave: Low BC

BC = Ballistic Coefficient: 

BC=\frac{m}{C_{D}A}

, C_D: Drag Coefficient, A: exposed area

Drag Force:

F_{D}=\frac12\rho V^2C_{D}A

deceleration induced by drag:

a_{D}=\frac12\frac{\rho V^2C_{D}A}{m}

Heating Rate a re-entry vehicle experiences:

q_{dot}=1.83\cdot10^{-4}V^3\sqrt{\frac{\rho}{r_{nose}}}

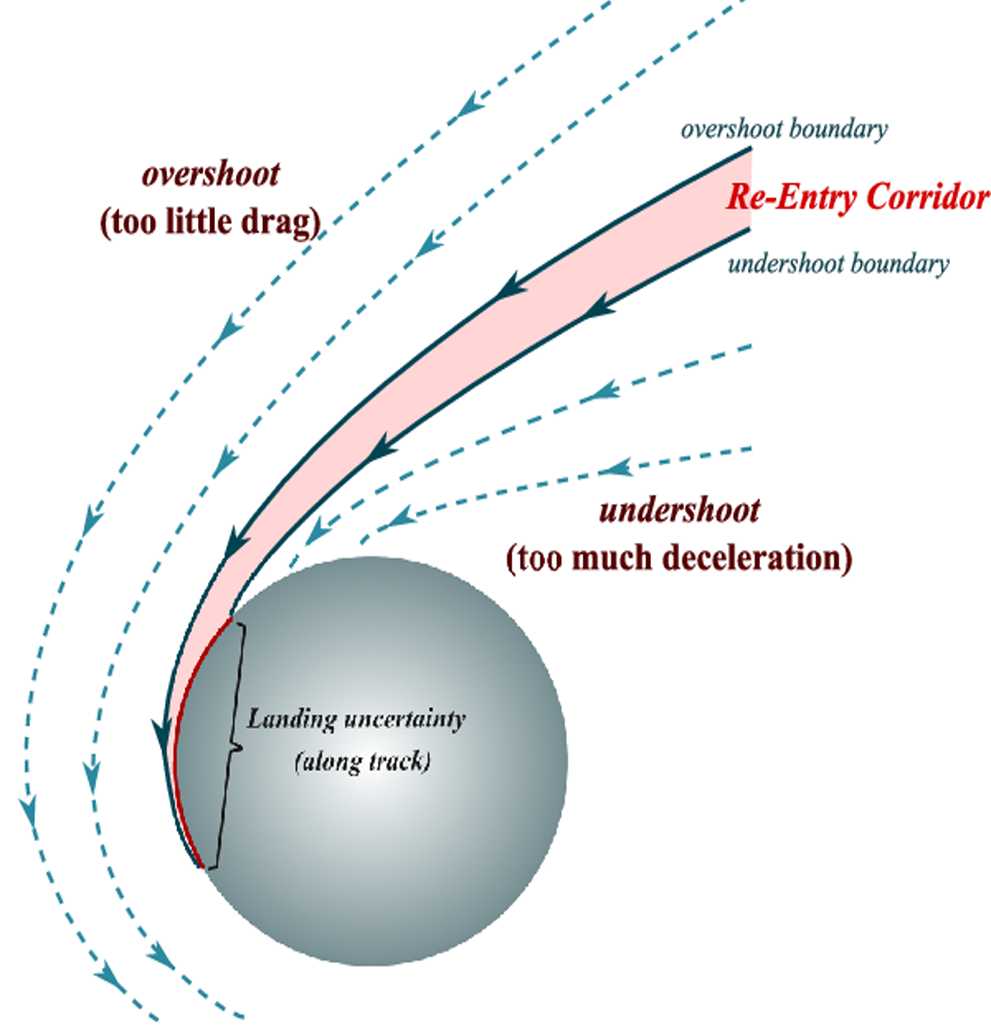
Re-entry Corridor

→A three-dimensional re-entry corridor through which a re-entry vehicle must pass to avoid skipping out or burning up

Re-entry Requirements

• Trajectory design: re-entry velocity, re-entry flight path

  • Vehicle design: Vehicle size and shape (BC), Thermal-protection systems

Aerobraking

Spaceflight technique wherein an orbiting spacecraft brushes against the top of a planetary atmosphere

The friction of the atmosphere against the surface of the spacecraft slows down and lowers the craft's orbital altitude

The solar panels are used to provide the maximum drag

→ Saves Cost and Mass