8/27 Pre Lecture Videos (Bitwise Logic Operations, Integer Arithmetic Overflow, Bit-Level Shift Operations, Integer Casting)

Bitwise Logic Operations

Examples: (Variables A and B are N-bit signed/unsigned built-in data types

• A & B

• A | B

• ~A

• A ^ B

Explain the steps to perform bitwise operations starting from hex

1. Convert the hex number to binary

2. If a ‘not’(~) operation, write the complement of each digit

   Otherwise (there are 2 numbers), align bit vectors and write the result of the operation of each digit

3. Convert back to hex

ANDing

The use of the bitwise AND operation for Masking groups of bits

• Ex. 10101110 & 00001111 = 00001110

• Selects last 4 bits

ANDing brings all the bits you had back (yield back 1) if you mask with 1s. If you mask with 0s, then all the bits you don’t need are gone (yield 0)

For Clearing groups of bits

• 10101110 & 00001111 = 00001110

• 0’s clear first 4 bits

It’s kinda like an editor for bits

a ∧ True = a

a ^ False = False

ORing

useful for “setting” groups of bits

• ex 10101110 | 00001111 = 10101111

• 1’s set last 4 bits

• 0s don’t change anything

a ∨ False = a

a ∨ True = True

XORing

Useful for “complementing” (inverting) groups of bits

• ex 10101110 ^ 00001111 = 10100001

• 1s invert last 4 bits

• 0s return the initial bit (it doesn’t change anything)

a ⊕ True = ~a

b ⊕ False = b

When does Signed Arithmetic Overflow occur?

When the sum of two signed integers >max value or <min value

What happens as a result is that the value goes back down

7 + 7 in a 4bit 2s complement will result in -2 instead of 14 because the max is 7

How can we detect when signed arithmetic overflow has occured in 2s complement?

[Positive Int] + [Positive int] = [Negative Int]

[Negative Int] + [Negative Int] = [Positive Int]

When does Unsigned arithmetic Overflow occur?

Sum of two unsigned integers > max value that can be represented by N number of bits

How can we detect Unsigned arithmetic Overflow

If the MSB Carry-out bit is one

If the carry-out is zero, then there is no overflow

Carry Out is the “carry the 1” thing

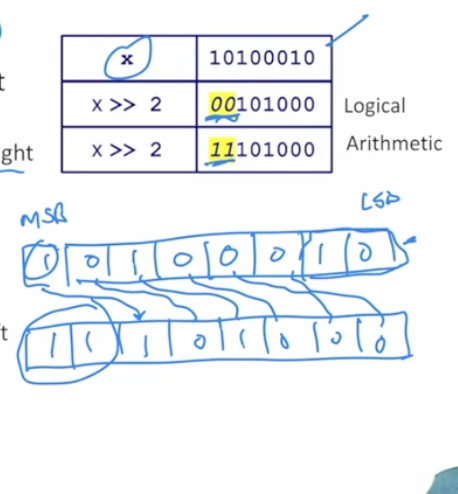
Bitwise Right Shift Operation

x >> y

• Shift x to the right by y bit positions

• Throw away extra bits on right

• Pad with 0’s on left (always logical)

Bitwise Left Shift Operation

x << y

• Shift x to the left by y bit positions

• Throw away extra bits on left

• Pad with 0’s on right (always logical)

Logical Shift

Pad with 0s on left

IF unsigned data type

Does it work with left shift? I don’t think so because it wouldn’t need to pad anything on the left.

Arithmetic Shift

Pad with value of MSB on left

If Signed Data type (This way, we preserve the sign from the MSB)

Bitwise Shift: Multiplication CONFUSING

• u << k gives u * 2^k

• Shifting u left by k digits, is u times the power of whatever the shift amount is

• Logic Shift does not preserve the sign-bit; so this multiplication rule doesn’t apply to that

Most machines

• shift and add/sub instructions are faster than a multiply instruction

How does (u << 5) - (u << 3) = u *24 ?

Bitwise Shift: Division

u > > k gives floor(u / 2^k)

• Logical shift does not preserve the sign bit

• Arithmetic shift preserves the sign bit (2s complement)

What does casting ultimately do?

Change the interpretation of the MSB

How can we avoid the mistake of converting a negative integer into a positive integer when performing an unsigned cast operation?

Use the Absolute Value Format

• abs() stdlib Library when data type is a signed integer

• fabs() in the math library when the data type is a floating-point value