final calculus exam COMBINED WITH THE EXAM 3

sequence

a list of numbers written in a mathematical order

harmonic series. diverge/converge?

diverge

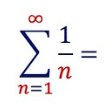
what two things indicate an alternating series?

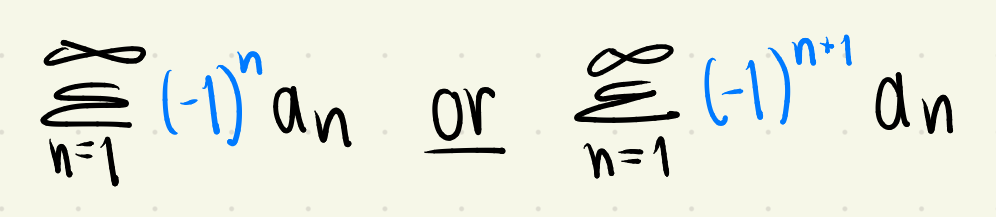
p-series

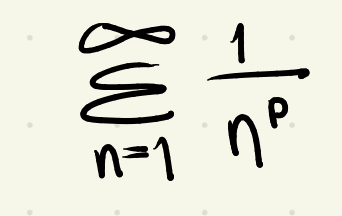
geometric series

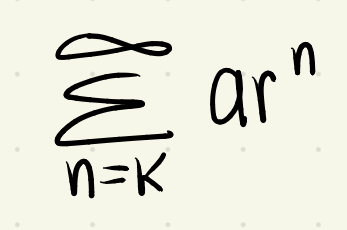
the p-series test

the geometric series test

the divergence test

when is the divergence test inconclusive?

if the limit equals zero, the test tells you nothing. the test can only tell you if it diverges, not converges

the integral test

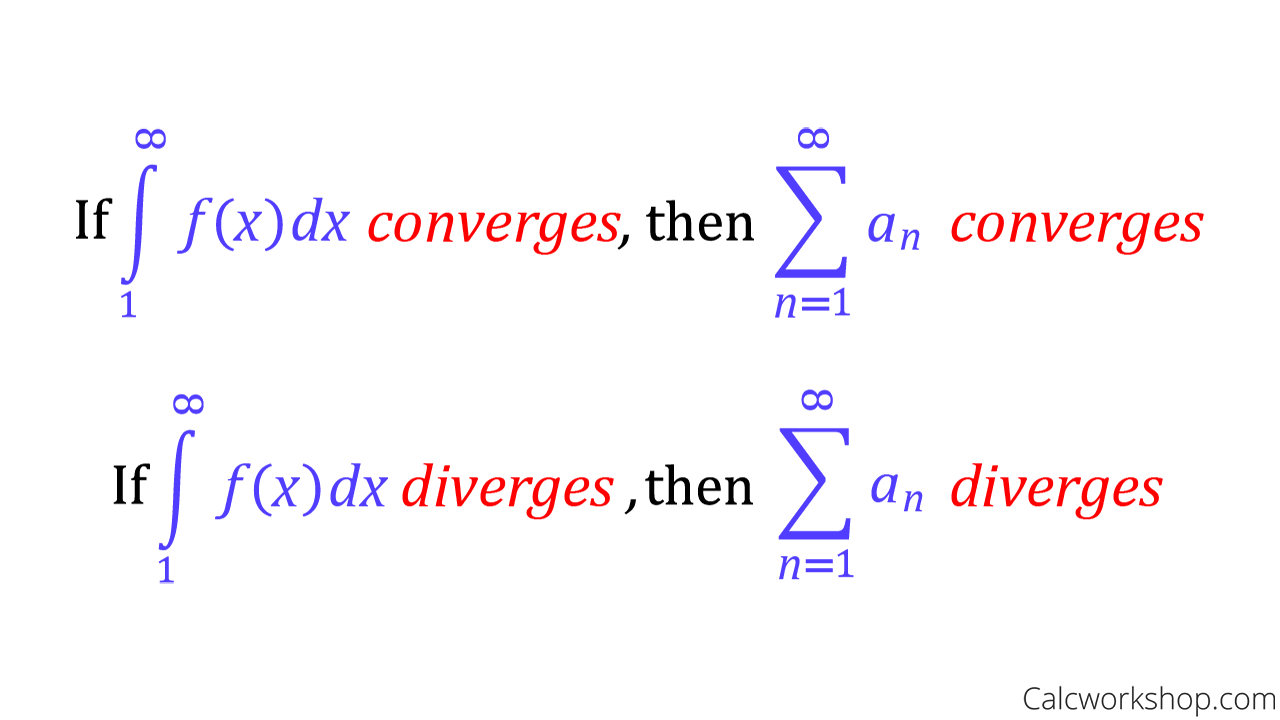
what are the conditions to the integral test?

f(x) must be positive, decreasing, and continuous on [1, infinity)

the comparison test

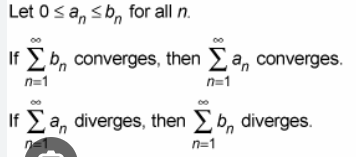
the limit comparison test

for BOTH comparison tests, what condition must be satisfied?

must be positive

the alternating series test

what are the conditions to the alternating series test?

positive terms, decreasing, limit is 0 (terms go to 0)

the ratio test

how to test for absolute convergent?

absolute value bars

the root test

the alternating harmonic series. diverge/converge?

Converge

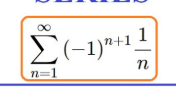
1

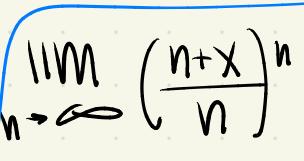
=e^x

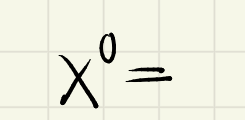
ANY non zero number to the 0 power will always equal?

1

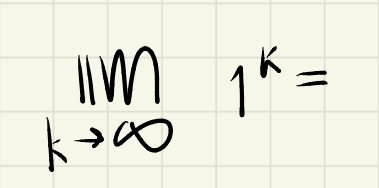
the limit of 1 to the power of k as k approaches infinity will always be?

1

when you write the interval of convergence and use a square bracket [, that indicates that it _______ at that endpoint

converges

the series converges for all x values has WHAT interval of convergence? 

(−∞, ∞)

when is it better to use the RATIO test over the root test?

when the series has a factorial in it

graph of ln(x)

how do i get from the position → velocity → acceleration function?

derive

displacement formula

the integral of the velocity function from a to b

displacement being equal to the position function at “b” - the position function at “a” is rooted in what theorem of calculus?

fundamental theorem of calculus

total distance traveled formula

the integral of the velocity function with absolute value bars

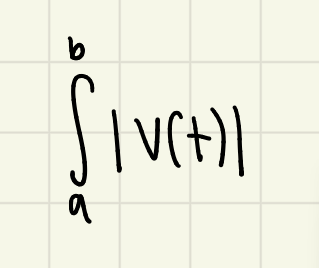
f(x)=x is what kind of graph?

linear

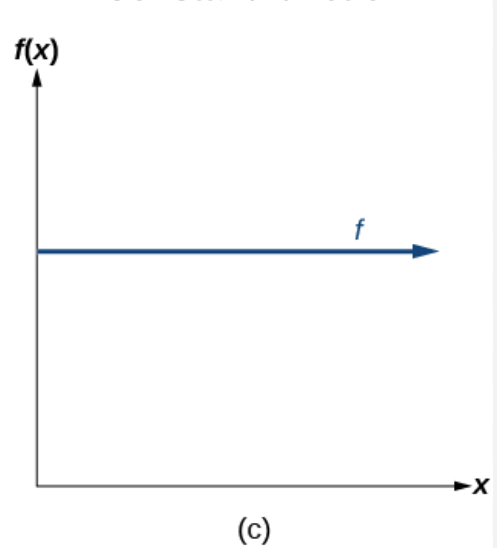
f(x)=c is what kind of graph?

constant (horizontal line)

f(x)=x² is what kind of graph?

quadratic (parabola)

f(x)=x³ is what kind of graph?

cubic

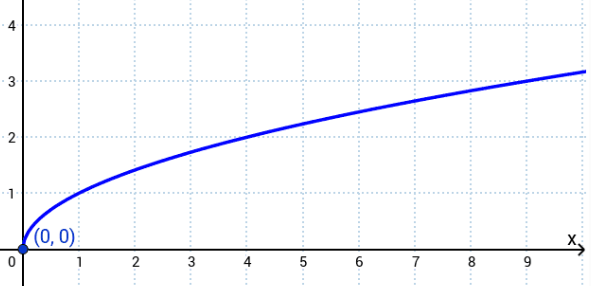
f(x)=square root of x is what kind of graph?

square root

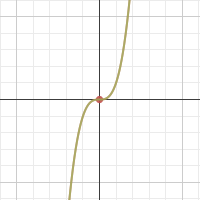
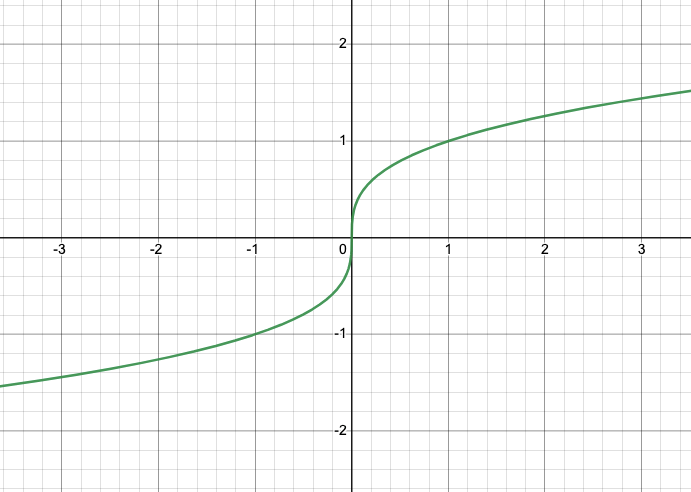
f(x)=cube root of x is what kind of graph?

cube root

f(x)=|x| is what kind of graph?

absolute value

f(x)=1/x is what kind of graph?

reciprocal

f(x)=a^x is what kind of graph?

exponential

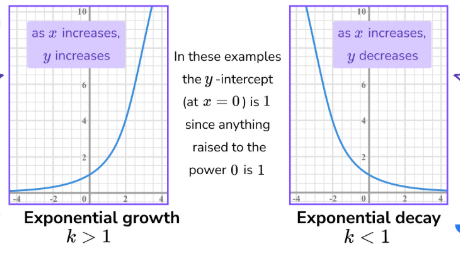
f(x)=logax is what kind of graph?

logarithmic

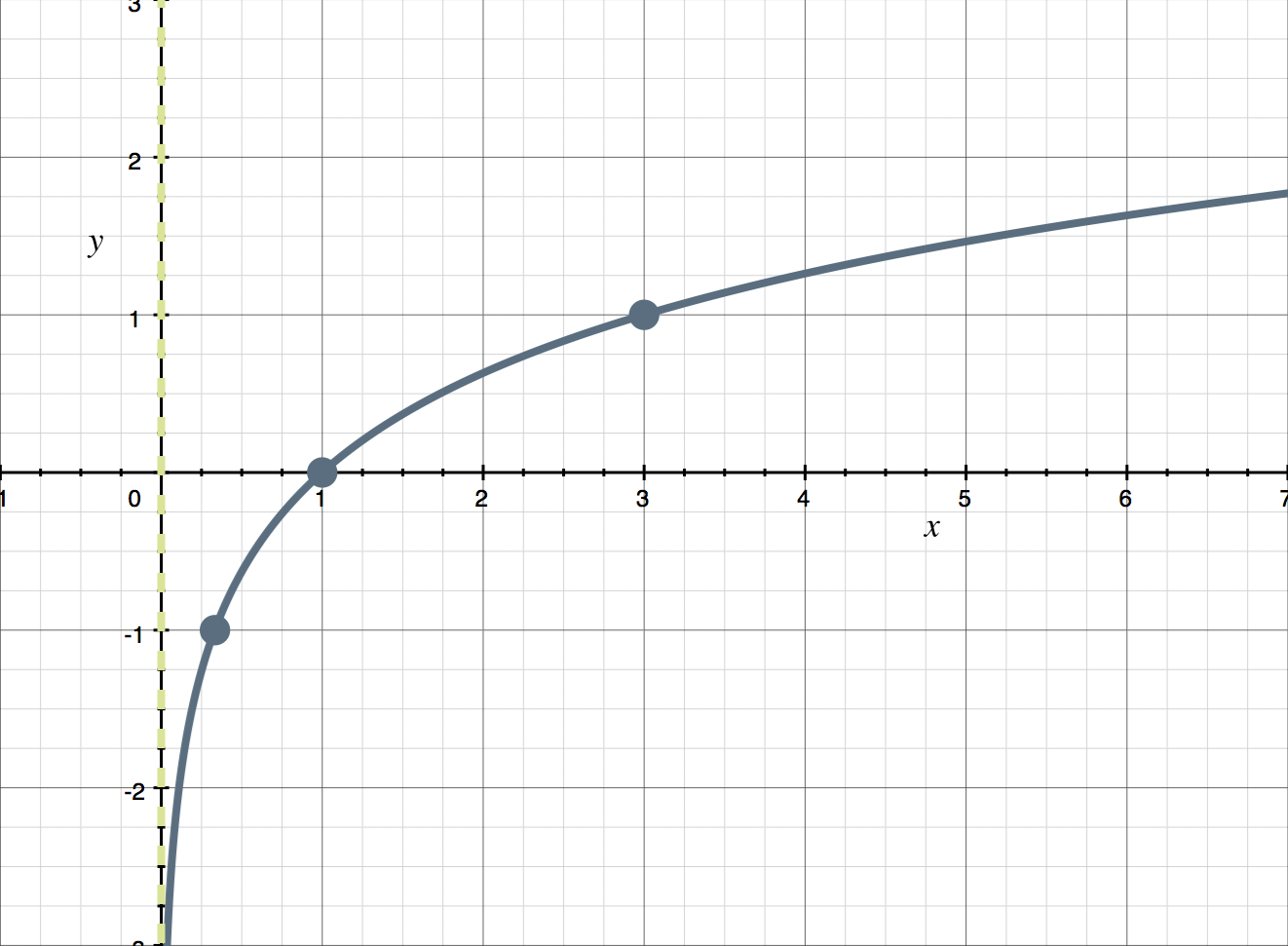
mass (integral) formula

the integral from a to b of density

shell method formula

the integral from a to b of 2(pi)r times (top-bottom)

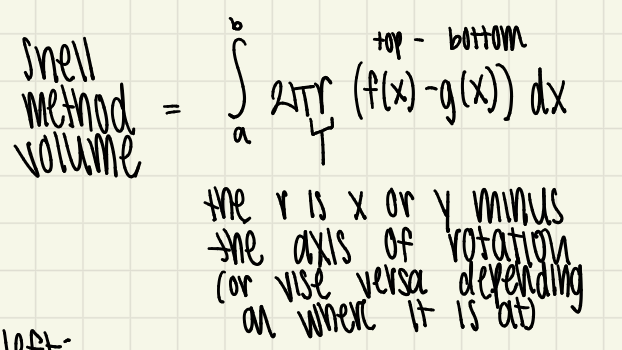
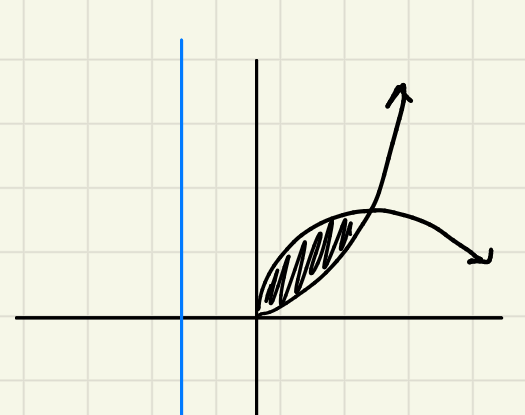
for the shell method: how would you write your “r” if the axis of rotation is to the left of the region?

r= x-axis of rotation

for the shell method: how would you write your “r” if the axis of rotation is to the right of the region?

r= axis of rotation -x

for the shell method: how would you write your “r” if the axis of rotation is below the region?

r=y- axis of rotation

for the shell method: how would you write your “r” if the axis of rotation is above the region?

r= axis of rotation - y

for the shell method the bounds will be ________ (perpendicular/parallel) to the axis of rotation?

perpendicular

when the axis of rotation is vertical: dx

when the axis of rotation is horizontal: dy

for the washer method the bounds will be ________ (perpendicular/parallel) to the axis of rotation?

parallel

when the axis of rotation is vertical: dy

when the axis of rotation is horizontal: dx

washer method formula

the integral from a to b of pi times the outer radius squared minus pi times the inner radius squared

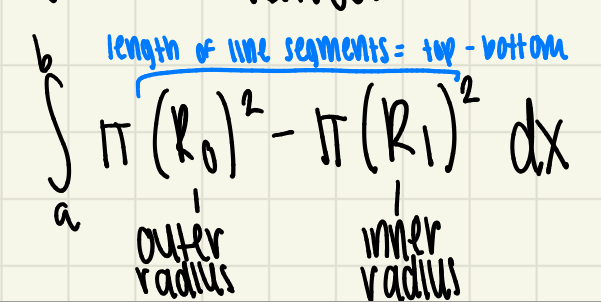
speed (from velocity function) formula

|v(t)|

disk method around the x-axis formula

the integral from a to b of pi times r(x)²

disk method around the y-axis formula

the integral from a to b of pi times r(y)²

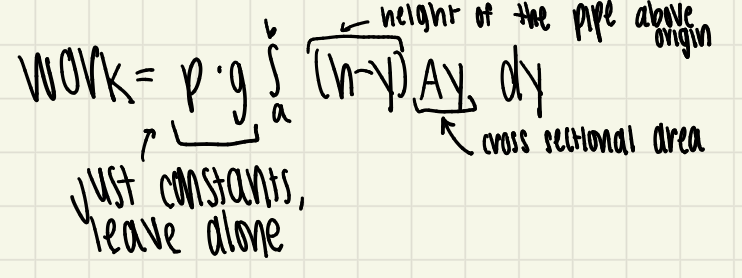
work formula

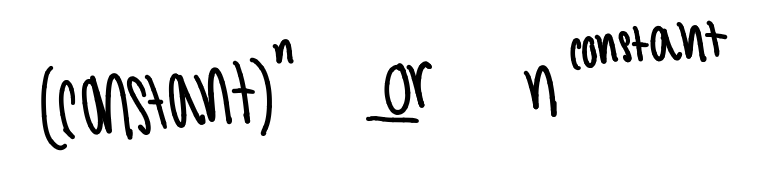
which term “grows” faster as n approaches infinity?

constant^n

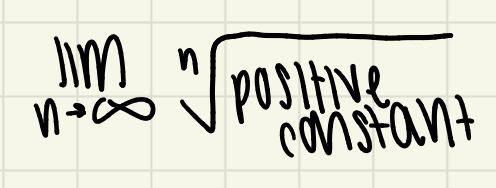
what is the limit as n approaches infinity for the nth root of a positive constant?

1

what is the integral of secx?

ln|secx + tanx| + C

cscx can also be written as?

1/sinx

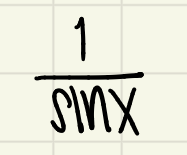
secx can also be written as?

1/cosx

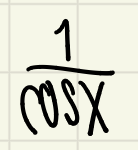
cotx can also be written as?

1/tanx

what is the derivative of secx?

secxtanx

what is the derivative of tanx?

sec²x

what is the integral of tanx?

ln|secx| + C