EMF Compleet

Efficient Market Hypothesis (EMH)

A theory that states that asset prices reflect all available information, making it impossible to consistently achieve higher returns than average.

Weak Form EMH

The hypothesis that stock prices reflect all past trading information, implying that technical analysis cannot yield consistent excess returns.

Semi-Strong Form EMH

The hypothesis that stock prices reflect all publicly available information, including past and present data, meaning fundamental analysis cannot yield consistent excess returns.

Strong Form EMH

The hypothesis that stock prices reflect all information, public and private, indicating that even insider information cannot provide a return advantage.

Abnormal Returns

The returns that differ from the expected return based on the market model or CAPM.

Cumulative Abnormal Return (CAR)

The total abnormal returns over a specified time period related to a particular event.

Event Study

A research method used to assess the impact of a particular event on the value of a firm, typically by analyzing the stock price changes.

Mean-Adjusted Model

A method used to calculate normal returns as the average return of the stock over a specified estimation period.

Market-Adjusted Model

A method that calculates normal returns based on the overall market return at each point in time.

CAPM (Capital Asset Pricing Model)

A model that establishes a linear relationship between the expected return of an asset and its risk, measured by beta.

Panel Data

Data that involves multiple observations over time for the same entities, allowing for various econometric analyses.

Random Effects Model

An econometric model in which the intercept varies across entities and is assumed to be random, allowing for the inclusion of time-invariant variables.

Autocorrelation / Serial correlation

Autocorrelation – also known as Serial Correlation – refers to the correlation between a variable and its own past values in a time series. In other words, it’s a measure of the degree to which a variable is correlated with its lagged (previous) values:

Unit Root

A characteristic of a time series that indicates non-stationarity, implying that shocks to the series have permanent effects.

Autoregressive (AR) Model

A time-series model that uses past values of a variable to predict its current value.

ARCH (Autoregressive Conditional Heteroskedasticity) Model

A model used to describe the volatility of a time series, where current volatility is a function of past squared returns.

GARCH (Generalized Autoregressive Conditional Heteroskedasticity) Model

An extension of the ARCH model that includes lagged values of both the squared returns and the estimated variance.

Bias-Variance Tradeoff

The balance between the accuracy of a model (bias) and its ability to generalize to new data (variance) in machine learning.

LASSO (Least Absolute Shrinkage and Selection Operator)

A regression analysis method that performs both variable selection and regularization to enhance prediction accuracy.

What are the main steps in conducting an event study?

1. Identify the event and its timing. 2. Specify a benchmark model for normal stock return behavior. 3. Calculate and analyze abnormal returns around the event date.

What is the market model residual approach to calculate abnormal returns?

It defines abnormal returns as the residuals from a regression of stock returns on market returns, accounting for the stock's beta.

What is the Fama-MacBeth procedure used for?

To estimate parameters in panel data regressions by averaging coefficients over time and adjusting for serial correlation.

What is the Fama-French three-factor model?

A model extending the CAPM by adding size and value factors to explain stock returns: SMB (Small Minus Big): Small firm returns minus large firm returns. HML (High Minus Low): High book-to-market ratio returns minus low.

How does the Newey-West correction adjust standard errors?

It corrects for heteroskedasticity and autocorrelation in regression residuals.

What are the advantages of using panel data?

1. Captures both time-series and cross-sectional variation. 2. Controls for unobservable variables constant over time or entities. 3. Allows for studying changes in relationships over time.

What is the difference between fixed effects and random effects models?

Fixed effects: Intercepts vary by entity but are constant over time. Random effects: Intercepts are drawn from a common distribution and vary cross-sectionally.

How are cumulative average abnormal returns (CAAR) calculated?

CAAR = (1/N) ΣCAR_i.

What is the role of t-tests in event studies?

To test whether abnormal returns are significantly different from zero.

How does the Fama-French three-factor model extend CAPM?

By including SMB (size effect) and HML (value effect) factors alongside market returns.

What is the key assumption of the fixed effects model in panel data?

The constant term varies across entities but remains constant over time.

What is the formula for market model residual abnormal returns?

AR_it = R_it - (α + β R_mt).

Why is event clustering a problem in event studies?

It causes cross-sectional correlation, invalidating standard t-tests.

What is the main advantage of the random effects model in panel data?

It allows for time-invariant variables and fewer parameters than fixed effects.

What are heteroskedasticity and autocorrelation consistent (HAC) standard errors?

Adjusted standard errors that correct for heteroskedasticity and serial correlation.

What is the purpose of the sign test in event studies?

To test whether there are as many positive as negative abnormal returns, assuming symmetry.

What are rank tests used for in event studies?

To account for the magnitude of abnormal returns without normality assumptions.

What is the calendar time returns method?

A long-horizon event study approach that regresses portfolio returns on risk factors over time.

What are buy-and-hold abnormal returns (BHAR)?

Returns calculated as the difference between the compounded realized and normal returns over a holding period.

Event induced variance

Events can introduce unexpected and volatile changes in asset returns, making it challenging to estimate their impact accurately (higher variance round the event date)

Event clustering

Multiple event occurring close together in time can complicate the attribution of returns to specific events and their effects. Induces cross-sectional correlation (and makes t-test invalid). However, good benchmark often solves this problem, if not two solutions

Standardized cumulative abnormal returns (SCAR)

SCAR is a measure that adjusts CAR for individual stock volatility, providing a normalized view of abnormal performance. Effectively dealing with differences in indiv. volatilities.

Advantages of using Panel data

This combination can help identify both temporal trend and variations among groups (firms), reducing the potential for omitted variable bias. Panel Data can address broader range of issues and tackle more complex problems with pure time series or pure cross-sectional data alone:

• Difference-in-Difference

• Regression discontinuity

Different panel data methods

Panel Data models, these approaches differ primarily in how the constant term and slope coefficients vary in the cross-section (i) and over time (t)

1.      Pooled OLS

No heterogeneity in α and β

2.      Seemingly unrelation regression (SUR)

3.      Fixed effects estimator

Constant term van varia cross i (αi)

Most popular in corporate finance/banking

4.      Random effects estimator

5.      Fama-Macbeth estimator

Constant and slope vary over time (αt and βt)

Most popular for models of asset returns

Pooled OLS

Simplest way to deal with panel data: estimate a single, pooled regression on all the observations together. Simply use all observations across i and t in a single regression.

Fixed Effects Model (FE)

Often used in finance. Slope coefficients the same across i (firms), but constant term allowed to differ across i; 

Can think of a αi as capturing all (omitted) variables that affect Yit cross-sectionally but do not vary over time.

Within Transformation

Also known as the fixed effects or demeaning transformation, involves adjusting the data to focus on within-entity variation. This transformation helps control for entity-specific (e.g. firm specific) effects, allowing for the analysis of within-entity variation over time while removing the overall entity-specific means.

How?:

• Take the time-series mean of each entity (firm):

  • Subtract this form the values of the variables yi1, …, yit

  • Do this for all entities I (e.g. firms) and for all explanatory variables

• Note that such a regression does not require an intercept term since now the dependent variable will have zero mean by construction

This model can be estimated using OLS

Time Fixed effects model

Capture the average effect of unobserved time-specific factors across all entities, heling control for time-specific variation while focusing on within-entity changes over time.

Clustered standard errors

Are a modification of standard errors in regression analysis to account for potential correlation or heteroskedasticity within groups or clusters in data. Error terms are allowed to be correlated within each cluster, but assumed not to be correlated across clusters.

Multi Factor models

Are financial models that extend the CAPM by incorporating multiple factors to explain the returns of assets (rather then only using the betas).

Autocorrelation (serial correlation)

Refers to the correlation of a variable with itself over successive time intervals. It indicates how the value of a variable at one time is related to its values at previous times, which can affect the accuracy of statistical models.

Asymptotic normality

Is a statistical property stating that as the sample size becomes large, the sampling distribution of a parameter estimate approaches a normal distribution. This is a key result of the Central Limit Theorem and is commonly invoked in statistical inference when dealing with large samples.

The Bera-Jarque Normality Test

Is a statistical test used to assess whether the residuals (errors) from a regression model follow a normal distribution. The test is based on the skewness and kurtosis of the residuals.

What do we do if we find evidence of Non-Normality in a small sample?

Sometimes one can transform the dependent variable (for example, transform size of firms to log of size, to counter extreme outcomes). Often, we also observe one or two outliers (extreme outcomes) causing us to reject the normality assumption. We can solve this by:

1.      Winsorize data: put lower and upper bound on a variable (say 1% and 99% percentile)

2.      An alternative is to use dummy variables

The Breusch-Godfrey Test

Is a statistical test used to detect the presence of serial correlation in the residuals of a regression model, especially in time series data. The test is an extension of the Durbin-Watson test and can be applied to assess higher-order autocorrelation.

Steps of a Breusch-Godfrey test

The null and alternative hypothesis are:

H0: p1=p2=pr=0

H1: pr is not 0

Step 1: Estimate the linear regression using OLS and obtain the residuals

Step 2: Regress u-hat on all of the regressors from stage 1 (the x’s) plus

              obtain R² from tis regression

Step 3: It can be shown that

If test statistic exceeds critical value from the statistical tables, reject the null

Weak dependence

Refers to the property of a time series where observations at different time points are not highly correlated. As the time lag between observations increases, the autocorrelation between them decrease relatively quickly

Covariance stationary

Is a property of a time series process where the mean and covariance structure of the series do not change over time. The covariance between observations at different time points depends only on the time difference, not on the absolute time

Why use lagged effects?

Inertia of the dependent variable / delayed response due to illiquidity

The dependent variable may not respond immediately to changes in the independent variable (processing time, transaction delays, or illiquidity in the market)

Overreaction / underreaction

Investor or economic agents might not immediately incorporate new information into their decision-making (sudden positive earnings surprise for a company, stock prices might initially overreact)

Reduce serial correlation of the error term

In financial time series, stock prices might be correlated with their own past values. Including lagged prices in a regression helps account for this correlation and produces more reliable estimates

Issue with lagged effects

OLS may become biased (but still consistent, that is, it approaches the true parameters as the sample becomes very large)

Reasons for measurement errors

• Macroeconomic variables are almost always estimated quantities (GDP, inflation, and so on), as is most information contained in company accounts.

• Financial market prices may contain noise if markets are illiquid

• Sometimes we have to estimate explanatory variables

  • E.g. if we want to use CAPM beta as explanatory variable

Stability tests

assess whether the statistical properties of a model (time series analysis or forecasting) remain consistent over different periods of time.

How to do a stability test

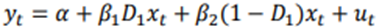
Stationary variables

Is a time series variable whose statistical properties remain constant over time. In a stationary time series, the data points exhibit stability and do not display systematic trends or seasonality. A stationary variable is a variable

• Without trends

• Stable variance over time

• Stable autocorrelation structure over time

• No periodic fluctuations (no seasonality)

Why care if a variable is stationary?

The standard OLS assumptions imply stationarity for the error term

If a variable is not stationary, OLS will give spurious and false results (unreliable)

It also matters for forecasting if a variable is stationary. Stationary time series often exhibit mean-reverting behaviour, meaning they tend to return a stable mean over time. This characteristic makes forecasting more meaningful and accurate, as the series is expected to revert to its long-term average

Autocovariance

Is a statistical concept that measures the covariance between observations of a random variable at different points in time, specifically within a time series. It quantifies the degree of linear dependence or relationship between the values of a variable at different time lags

A white noise process

it is a sequence of random variables that are uncorrelated and exhibit no discernible pattern over time.

Characteristics of a white noise process

1.      Independence – observations at different time points are not influenced by or correlated with each other. The occurrence of an event at one point does not provide information about the occurrence of an event at another time

2.      Constant Mean – the average or expected value of each observation is constant across all time points

3.      Constant Variance – the variability or dispersion of the observations remains constant over time

4.      Zero Autocorrelation – the autocorrelation between observations at different time lags is zero, except for observations at the same time point (which have an autocorrelation of 1)

the Ljung-Box or Portmanteau statistic:

tests the joint hypothesis that all m of τ_k autocorrelations are jointly equal to zero. Ensuring that residuals are white noise, a key requirement for accurate forecasting.

Autoregressive Model

is a type of time series model that expresses a variable as a linear combination of its own past values. In an autoregressive model, the current value of the variable is modelled as a weighted sum of its past values, which each past value multiplied by a coefficient.

Steps of an autoregressive model

1.      Understand the Data – begin examining the time series data to understand its characteristics, trends, and potential temporal dependencies

2.      Check stationarity – ensure that the time series is stationary

3.      Select the Order (p) – a autoregressive model of order p, an AR(p) follows:

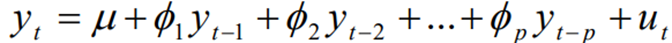
4.      Estimate the coefficients – use a suitable method (e.g., least squares) to estimate the autoregressive coefficients (Ф₁, Ф₂, …, Ф_p) by fitting the AR model to the time series data

5.      Goodness of Fit – involves examining residuals. With the standard OLS assumptions for the error term u

• Simples model: AR(1)

  

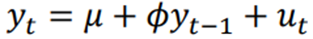
• We can show: if -1 < Ф  <1, then y is stationary

  • Then we can estimate μ and φ by OLS regression

How many lags to include in an AR model?

Use “information criteria”: Akaike’s (1974) information criterion (AIC), Schwarz’s (1987) Baynesian information criterion (SBIC)

Akaike’s (1974) information criterion (AIC), Schwarz’s (1987) Baynesian information criterion (SBIC)

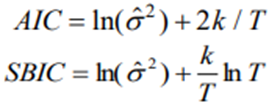
Use an AR model: obtain long-term impact of a shock to the variable (scenario analysis)

We call this Impulse Response Function (IRF) – quantifies the systematic response of each variable in the model of the shock on the variables, illustrating how they adjust over subsequent periods

In-Sample Forecasts

evaluate forecasts for the sample that you also used for estimating the forecasting model. One can expect these forecasts of the model to be good in-sample, since the model was fitted to these data. Not very informative on the true predictive power.

Out-Sample forecast

is useful to address the limitation of in-sample forecasts. Out-sample forecasts involve using the model to predict values for data point that were not part of the training set. Out-sample forecasts is a way to asses how well the model generalizes to new situations

training set

Is a subset of data used to teach or train a machine learning or statistical model. It consists of examples or observations with known outcomes, allowing the model to learn patterns and relationships between input features and the corresponding output.

Forecast approach - Expanding window

estimate the AR model using data form t = 1 to t = s, and then generate forecasts with this model. Repeat for all dates s

Forecast approach - Rolling window

  always use last k observations to estimate AR model and generate forecasts. Estimate model using data form t = s-k to t=s. Repeat for all dates s

Vector Autoregressive Model

is a type of statistical model that simultaneously considers multiple time series variables. Several autoregressive models working together, where each variable is predicted based on its own past values of other variables in the model. VAR models are used to capture the dynamic interactions and relationships between different variables over time.

Contemporaneous terms

Contemporaneous terms refer to variables, events, or phenomena that occur at the same time period in a given context, especially in statistical, economic, or time series analysis.

Non-stationary

describes a situation where the characteristics or properties of a process change over time, introducing variability and making predictions or analysis.

Spurious regression

occurs when two non-stationary time series exhibit a high correlation, leading to misleading results in regression analysis. (high R2 not always causation)

Type of non-stationary model (Stochastic trend) - Random Walk

is a time-series model where each value in the series is a random and unpredictable step away from the previous value. The basic idea is that future values are determined by the current values plus a random shock or error term

Type of non-stationary model - Deterministic trend

in contrast incorporates a systematic and predictable trend over time. It assumes that the data follows a clear and consistent upward or downward path.

3 cases for stochastic non-stationary

Based on the last formula, we then have 3 cases:

1.    Ф  1 => Ф^T 0 as T

So the shocks to the system gradually die away (stationarity)

2.    Ф  1 => Ф^T for all T

So shocks persistent in the system and never die away. We obtain:               

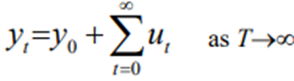
So just an infinite sum of past shocks plus some starting value of y₀

3.    Ф  1 => Ф³ Ф² Ф etc.

Now shocks become more influential as time goes on

How to “remove” the stationarity for a random walk process?

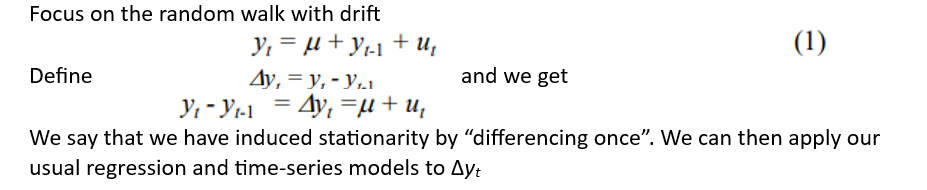
Test for Unit Root - Dickey Fuller test

1.    test the null hypothesis that Ф  1 in:

Again the one-sided alternative Ф1. So we have

              H₀: series contains a unit root

              H₁: series is stationary

Test for Unit Root - KPSS test

H₀: y_t is stationary

H₁: y_t is non-stationary

What to do with a process with an AR-coefficient close to 1?

• Often researchers take first differences, or focus on the error term u_t of an AR-model (y_t = Фy_t-1 + u_t)

  • If Ф is close to 1, then the first difference Δy_t and u_t are practically the same

Approaches to model volatility

Rolling Window Approach

Exponential Weighted Moving Average

ARCH/GARCH Models

Exponentially Weighted Moving Average (EMWA) - Volatility measuring

calculates the weighted average of a time series, giving more weight to recent observations and less weight to older ones. It assigns exponentially decreasing weights as you move back in time.