Principles of Modern Mathematics (All Units)

A Set

A collection of objects (colors, numbers, people) and is traditionally defined with a capital letter.
EX: set A, set B

Natural Numbers (N)

The numbers that are used for counting.
EX: (1,2,3,4,5...)

Real Numbers (R)

The numbers that lie along the number line; can be used to measure distance.
EX: (1,2,3,4,0,-1,-2,-3,-4, 3/2 π

Integers (Z)

A set in which you take all natural numbers, add zero and the negative numbers.
EX: {-3,-2,-1,0,1,2,3}

Rational Numbers (Q)

A set of all quotients or fractions in the form where both the numerator and the denominator are integers and the denominator cannot equal zero.
EX: 1/2, 3/4, 0, √81

Irrational Numbers (I)

A set of real numbers that cannot be expressed as a ratio of integers; you take away all rational numbers and zero cannot be in the denominator.
EX: π, √2, √8/23

Complex Numbers (C)

All numbers of the form where A and B are real numbers a+b√I=a+bi.
EX: 3+2i, 18+2i

Intersection of Sets (∩)

A set in which all elements belong to both A and B.
EX: {1,2,3,4,5} ∩ {4,5,6}= {4,5}

Union of Sets (∪)

A set in which all elements belong to either A or B. This is formed by taking every element in A then including every element of B that is not listed.
EX: {1,2,3,4,5,6,7} ∪ {2,4,6,8}= {1,2,3,4,5,6,7,8}

Complement of Sets (A')

The set of elements in the universal set that aren't in A'
EX:
U'= {1,2,3,4,5,6}
A= {2,4}
B= {1,3,5}

Element of a Set (aεA)

Objects in the set

Null Set (∅)

A set that does not contain any values or elements.

Cartesian Product (AXB)

The set of all ordered pairs with A' and B'
EX: A= {1,2,} B= {3,4,5}
(1,3), (1,4), (1,5)
(2,3), (2,4), (2,5)

Order ( IAI)

The order of a set A is the number of elements in the set A. EX: A= {1,2,3,4} IAI=4

Venn Diagram

Represents the relationships between sets in a problem using circles for the set and a rectangle for the universal set.

A not B (A-B)

The set A not the set B is the set of elements in set A that aren't in set B (order is important!)
EX:
A= {1,2,3,4,5}
B= {3,4,5}
A-B= {1,2}

Numerals

The symbols representing the numbers.

Positional System

The ultimate in efficiency and occurs in which only multipliers are used.

Face Value

The inherit value of the symbol.

Place Value

The power of the base that is associated with the position that the digit occupies.

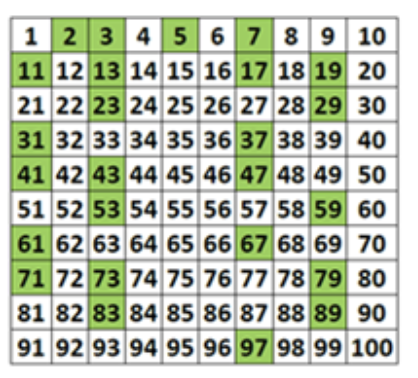
Prime Number

A number that is natural and >2 and when divided, the numbers are 1 and itself.

Multiplicative Identity

1 is the MI for all real numbers since 1 x a = a=a x 1

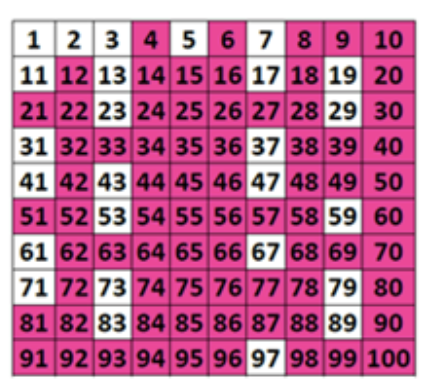
Composite Number

In which C is a natural number that is ≥ 4 if it isn’t a prime number.

The Fundamental Theorem of Arithmetic

Any natural number > 1 with a unique prime factorization.

Greatest Common Divisor

The lowest natural number that divides into both n&m.

OR

The smallest power.

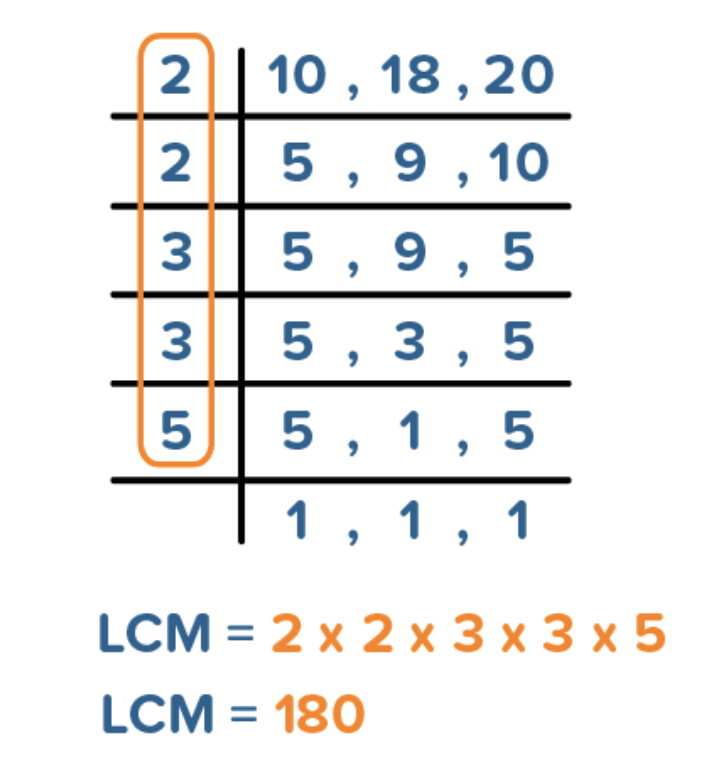
Least Common Multiple

The smallest natural number that is both a multiple of n&m.

OR

The biggest power.

Hindu Arabic System

Modern number system used by most cultures.

Base 10 Number System

Ten symbols representing quantity (0-9) and uses position to represent powers of 10

Base a Number System

a symbols representing quantity (0-9,a-1) and uses position to represent powers of a