Matrices

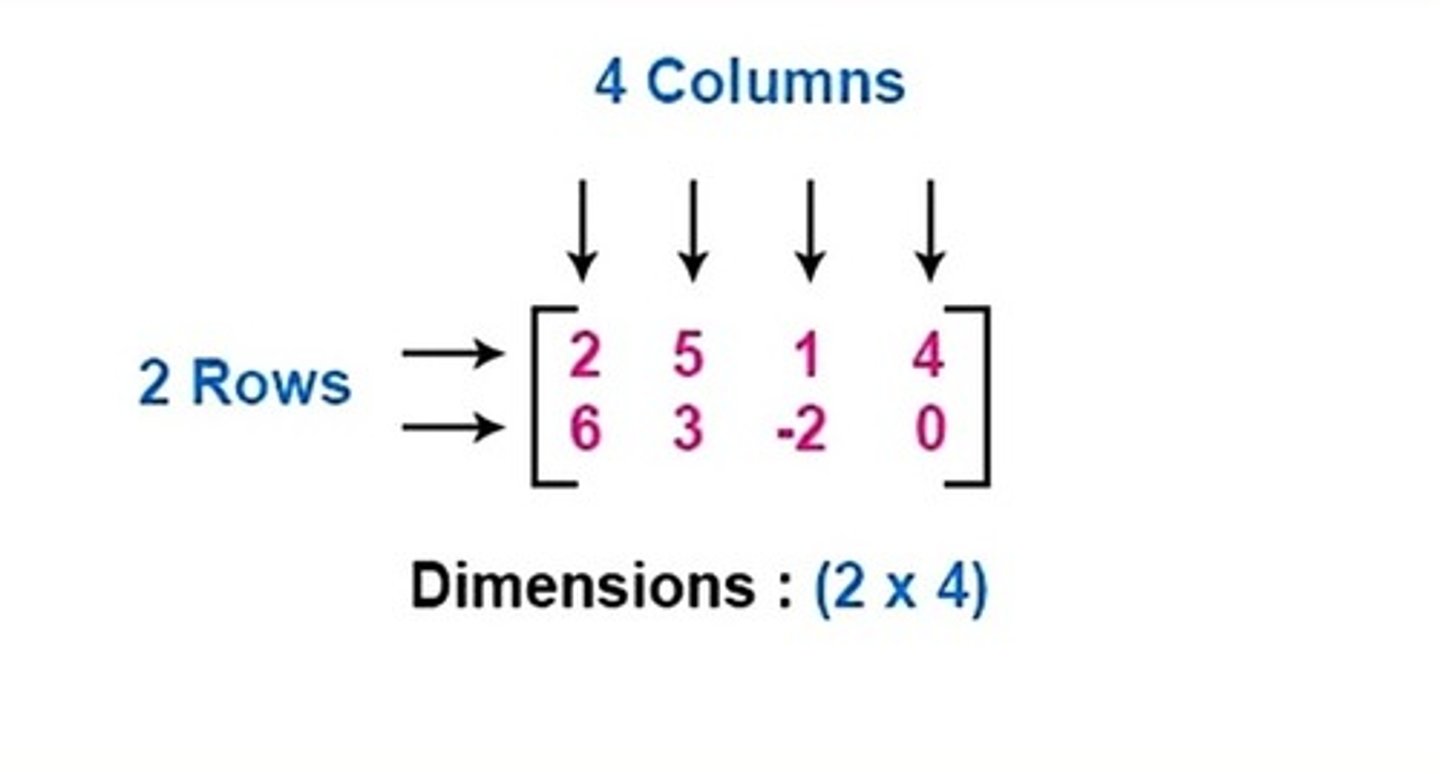
What is the Order of a Matrix?

Number of rows x Number of columns

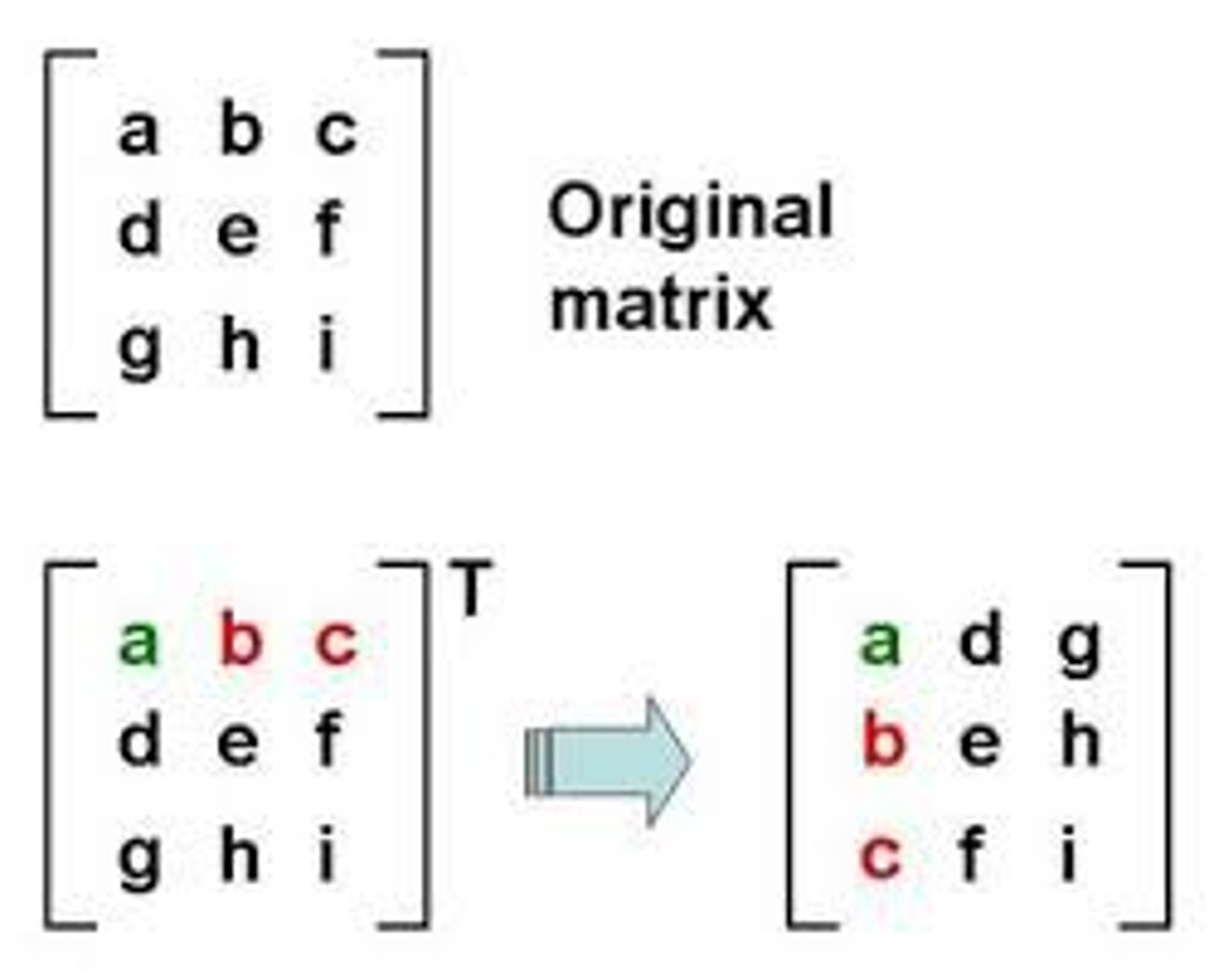
What happens when you Transpose a Matrix?

Row 1 becomes column one etc.

What is required in order for you to be able to add or subtract Matrices?

They must be the same size (additively conformable)

What is the Zero Matrix/Null Matrix?

What is the Identify Matrix, I?

[1 0]

[0 1]

or

[1 0 0]

[0 1 0]

[0 0 1]

etc.

What is required in order for you to be able to multiply Matrices?

The number of columns of the first matrix must equal the number of rows for the second.

e.g. 4 x 3, 3 x 2 will form a 4 x 2 Matrix

What does not commutative mean?

A x B ≠ BxA

A x A =

A^2

The equivalent of "1" is

the identity matrix, I

e.g. A x I = A

How do we divide Matrices?

We multiply by the Inverse.

Which Matrices can have an inverse?

Only square matrices.

A^-1 =

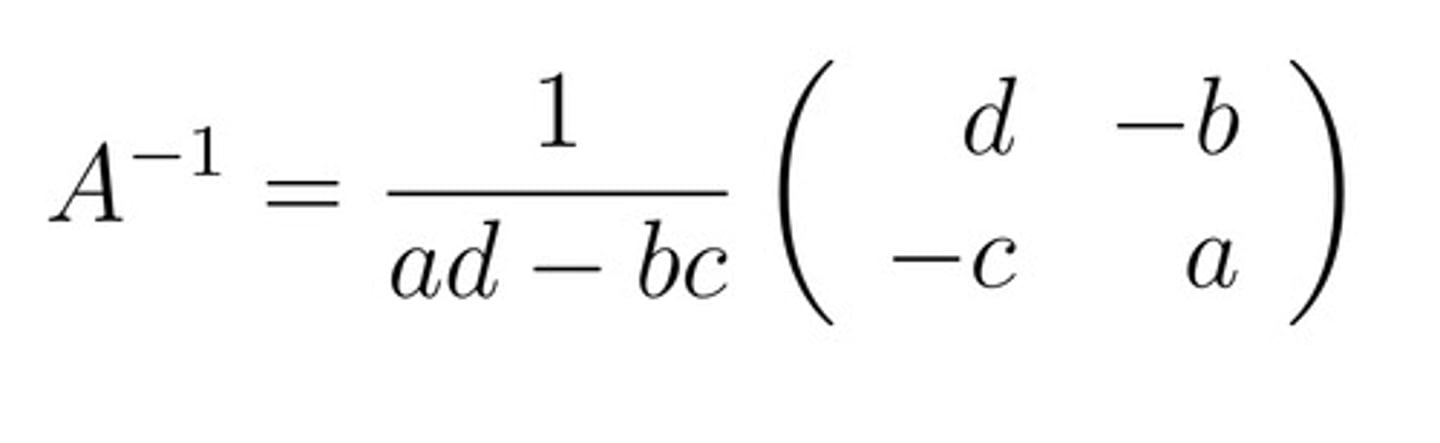
What is the determinant, det(A)?

ad-bc

What happens if the determinant equals zero?

There is no inverse it is a singular matrix.

What happens if the determinant does not equal zero?

There is an inverse it is a non-singular matrix

A x A^-1 =

Identity matrix, I

Determinant of a 3×3 matrix

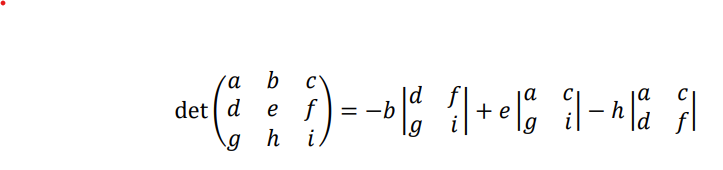
Matrix of minors

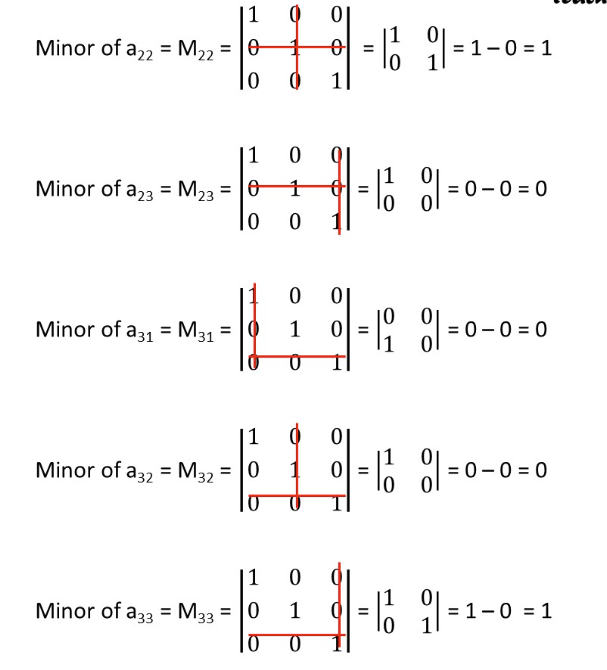
Matrix of cofactors

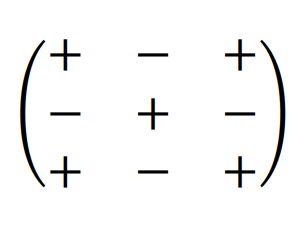
How to find inverse of a 3×3 matrix

If A(x) = v  then…                                                                                       (y)                                                                                                         (z)

(x) = A^-1 v

(y)

(z)

How to determine if equations are consistent

If there is at least one set of values that satisfy all equations simultaneously, else inconsistent

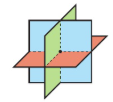
Shape formed if consistent equations with 1 solution

Planes meet at a singular point. Can only occur if matrix is non-singular (det ≠ 0)

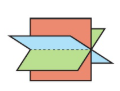
Shape formed if consistent equations with infinite solutions

The planes form a sheaf

Shape formed if inconsistent equations with no solutions

The planes form a prism

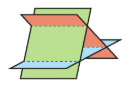
How to deduce parallel planes from equation

If one row of the matrix is a linear multiple of another