Lecture 3: Table & Graphs

data

• measurement/observations of variables of interest

datasets

• sets of info collected from multiple research participants

• set up in data matrix

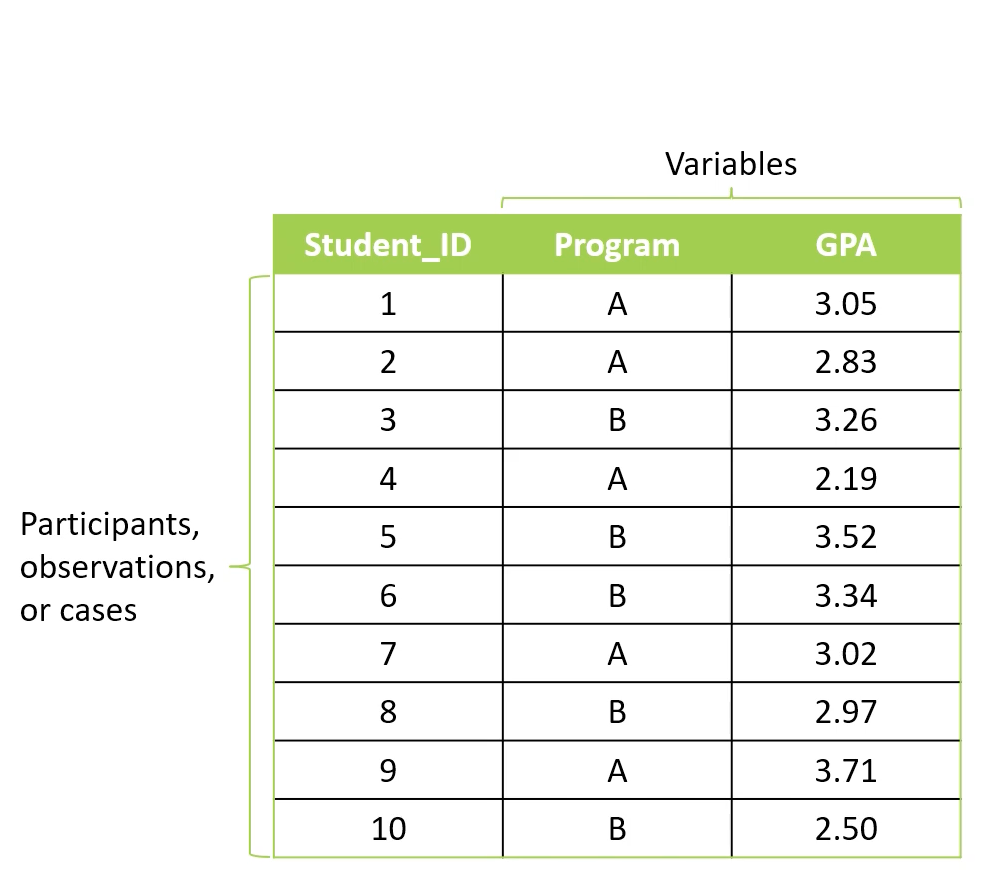
data matrix

• rows = participants

• column = variable measurements

• Student ID = observations/participants

• program + GPA = variables

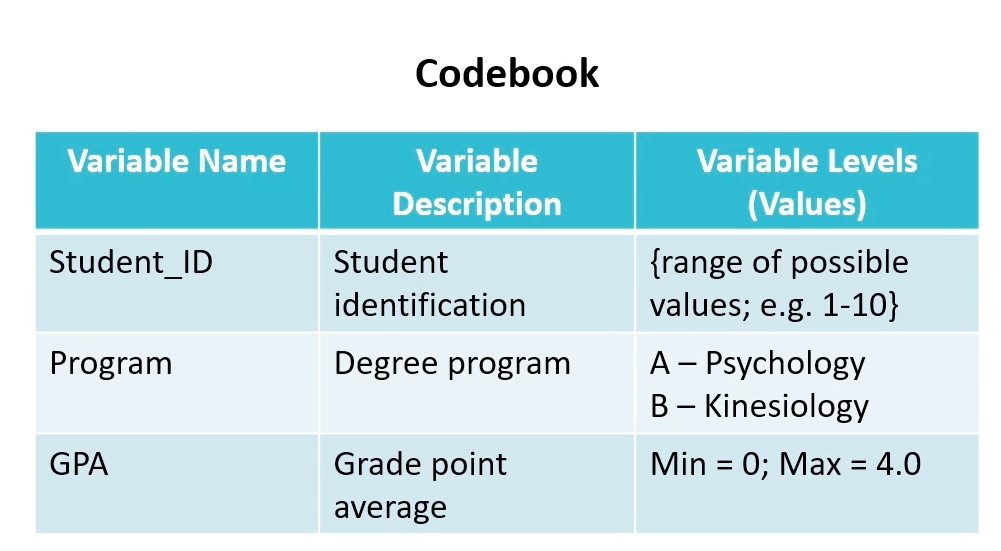
codebook

• detailed info re each variable in dataset or distribution

• variable levels = list all POSSIBLE values

why we should examine data

• gain initial sense of data as whole

• detect data coding/entry errors

  • values recorded accurately? impossible values?

• ID outliers (unusual, rare, extreme values)

• evaluate research methodology

  • were methods effective in measuring variables

• determine whether data meets statistical criteria/assumptions

  • shape distribution of measurements in data?

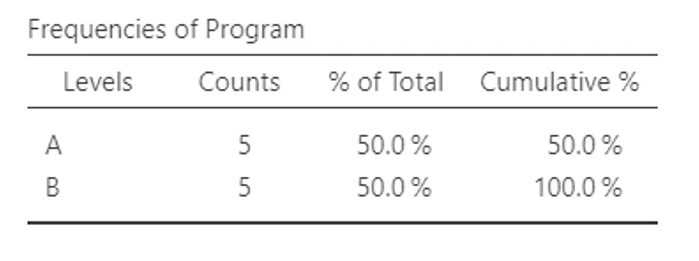
frequency distribution table

• summarizes the #/ and % of participants for each given level of a variable

  • for nominal, ordinal scales of measurement because fewer values posible

  • variable values

  • frequency (f)

  • percentage

% total formula

% = (f/N) x 100

• f = frequency

• N = total number of participants

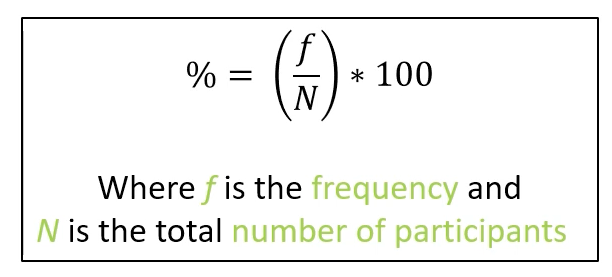
group frequency distribution table

• summarizes LARGER sets of data into SMALLER intervals/grouped values

  • useful for interval/ratio scales of measurement (many possible values)

  • variable values

  • frequency (f)

  • percentage

x-axis

variable values/levels (horizontal)

y-axis

frequencies (vertical)

bar graph

• categorical/discrete data

• nominal or ordinal

  • interval/ratio ONLY if created broader grouping categories

• bars do not touch = distinct categories

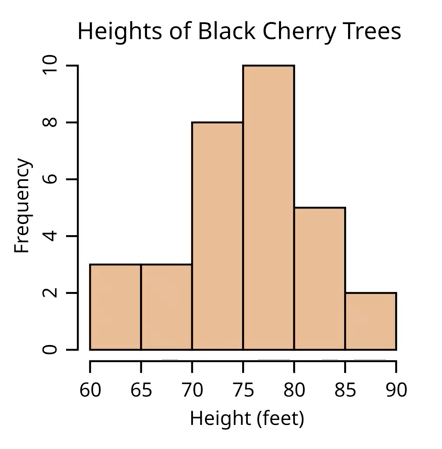
histogram

• continuous data

  • interval or ratio

• bars TOUCH to represent numerical continuity

smooth curve

• theoretical distribution

• height of curve = relative frequencies of variable levels

  • peak = highest relative frequency

  • tails = lower/decreasing relative frequency

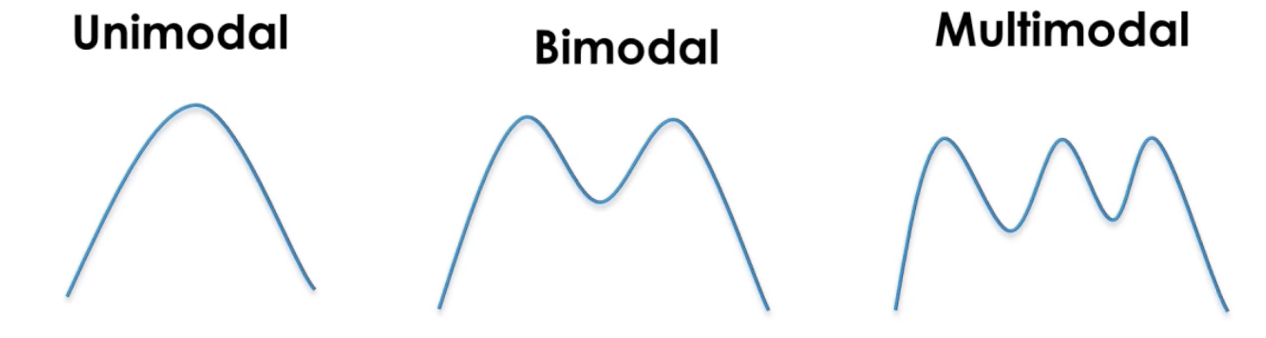
modality - describing shape of distribution

• what is the most frequent value

• 1 peak = unimodal

• 2 peaks = bimodal

• 3+ peaks = multimodal

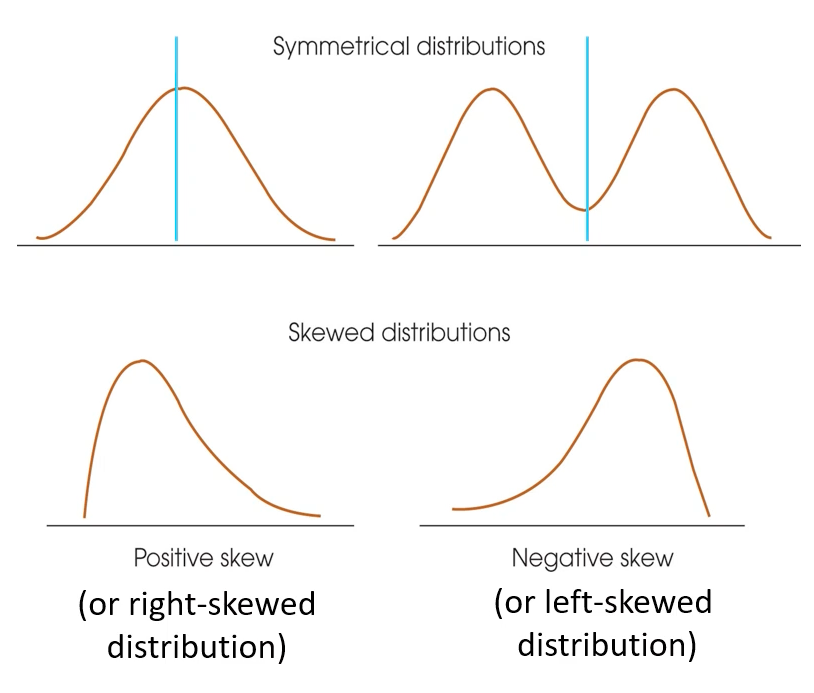
symmetry - describing shape of distribution

• is it symmetrical or asymmetrical

• symmetrical

  • possible to draw vertical line through middle so sides mirror images

• assymetrical/skewed

  • values pile up toward one end = taper off at tail of distribution

  • + skew = tail RHS

    • higher values occur LESS frequently, lower values occur more frequently

  • - skew = tail LHS

    • higher values occur more frequently and lower values occur less frequently

what does symmetry tell us?

• where MOST of the values lie (what type of distribution)

• require assumptions to be met

  • distribution is roughly symmetrical

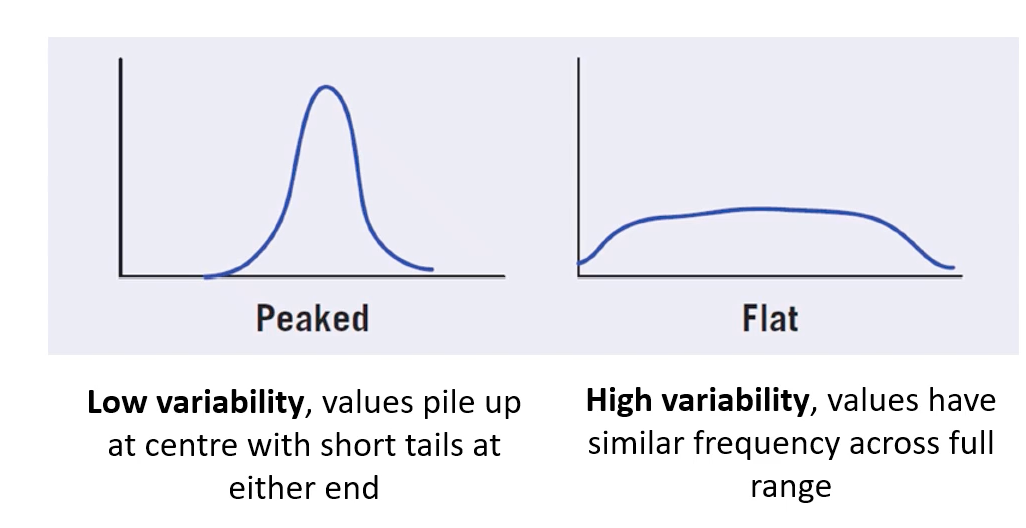
variability - describing shape of distribution

• how spread out are the data

• low

  • values pile at center = short tails at either end

• high

  • values have similar frequencies across full range