Waves 2

Superposition of waves

Overlap of two waves at a point in space

Principle of superposition (of waves)

When two waves meet at a point the resultant displacement at that point is equal to the sum of the displacements of the individual waves.

Superposition of waves

Overlap of two waves at a point in space

Principle of superposition (of waves)

When two waves meet at a point the resultant displacement at that point is equal to the sum of the displacements of the individual waves.

Interference

Superposition of two progressive waves from coherent sources to produce a resultant wave with a displacement equal to the sum of the individual displacements from the two waves

Constructive interference

Superposition of two waves in phase so that the resultant wave has greater amplitude than the original waves

Destructive interference

Superposition of two waves in antiphase so that the waves cancel each other out and the resultant wave has smaller amplitude than the original waves

Coherent waves/ waves sources

Waves/ waves sources that have a constant phase difference. For this to happen they must have the same frequency

Path difference

• The difference in the distance travelled by two waves from their source to a specific point

• Difference is often measured in wavelengths

Monocromatic wave (source)

(Source that emits) Waves of a single frequency

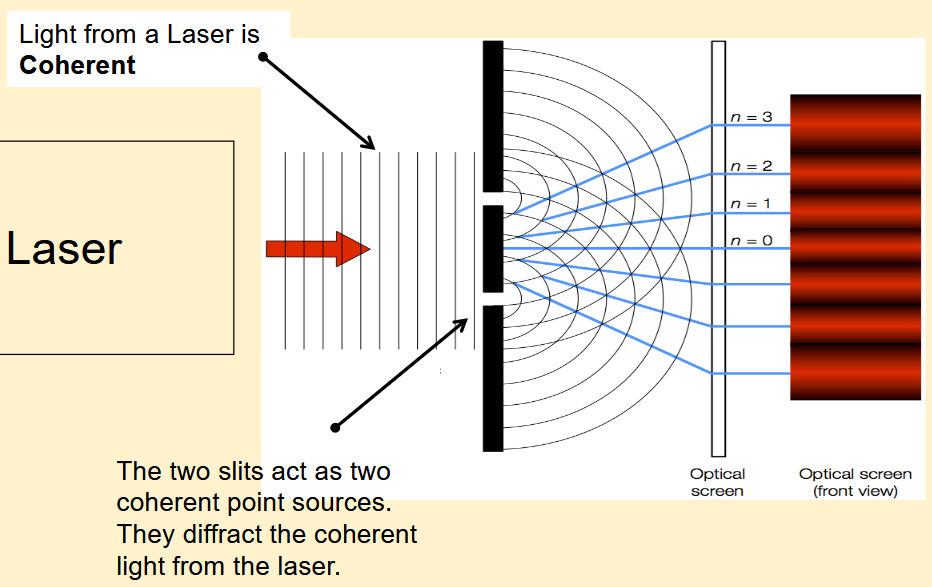
How you can obtain two coherent light sources from a laser

• Light from a Laser is coherent

• The two slits act as two coherent point sources. They diffract the coherent light from the laser.

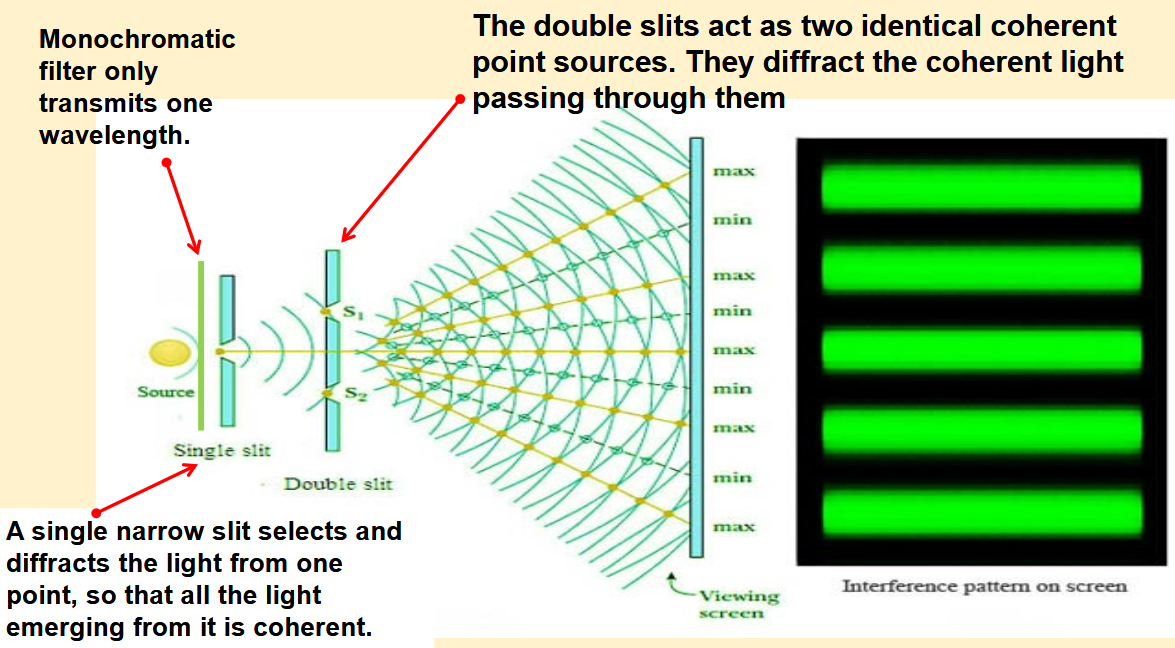
How you can obtain two coherent light sources from a white light filament bulb

• Place a monochromatic filter in fron of the bulb.

• The Monochromatic filter only transmits one wavelength.

• A single narrow slit selects and diffracts the light from one point, so that all the light emerging from it is coherent.

• The double slits act as two identical coheren point sources. They diffract the coherent light passing through them.

Young’s double slit equation

λ = ax/D

λ is the wavelength in metres, a is the slit separation in metres, x the fringe separation in metres, D is the distance between the slits and the screen in metres.

Youngs double slit experiment (diagram, equipment, method, analysis, uncertainties)

Aim of this experiment is to find the wavelength of a light source. λ is the wavelength, a is the slit separation, x the fringe separation, D is the distance between the slits and the screen.

Diagram:

• Shown above

Equipment:

• Laser

• Double slit

• White Screen

• Ruler

• Tape measure

• Travelling microscope

Method:

• To obtain two coherent sources shine light

  from a laser through a double slit.

• The equipment needs to be set up so that D is greater than 1m. Measure the distance D with a tape measure.

• Measing slit separation using a travelling microscope.

• To find fringe spacing x, use a ruler to measure the distance from the centre of the first dot to the centre of the last visible dot. Count the number of spaces between the dots. x = distance / number of spaces

• The distance is measured over a number of

  fringes to reduce the percentage uncertainty

  in x.

• Increase D and repeat measurements to determine the new value of x . Repeat for this at least 6 different D values

Analysis:

• Rearranging λ = ax/D gives x = λD / a

• Plot a graph of x against D: x = (λ/a)D + 0

• This should be a straight line through the origin

• The gradient is equal to λ/a. Rearranging gives λ = gradient × a

Uncertainties:

• The measurements of D, a and x all have uncertainties from the measuring instruments used. The absolute uncertainty in each remains constant, but the percentage uncertainty can be reduced. To do this, you can:

  • Increase D

  • For x, use x = distance / number of spaces, and measure the distance over a number of

    fringes

Monochromatic light / source / filter

Light of a single frequency / source that emitts single frequency / filter that transmitts a single frequency

Conditions necessary for the formation of a stationary wave

• Two waves that superpose

• Same wavelength or frequency

• Equal and opposite velocities

• Same or similar amplitudes

Key condition for harmonics to occur on string

• The length of a vibrating section of string is a whole number of half wavelengths

• Time for a wave to travel along the string & back is equal to the time for a whole number of waves

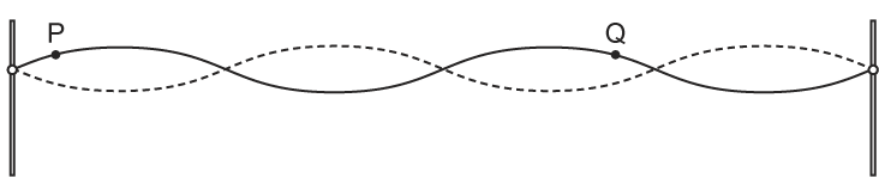
The diagram shows a string stretched between two posts. The string is plucked and a stationary wave is set up. What is the phase difference between P and Q?

• A: 0 rad

• B: π/4 rad

• C: π/2 rad

• D: π rad

Multichoice answer: A

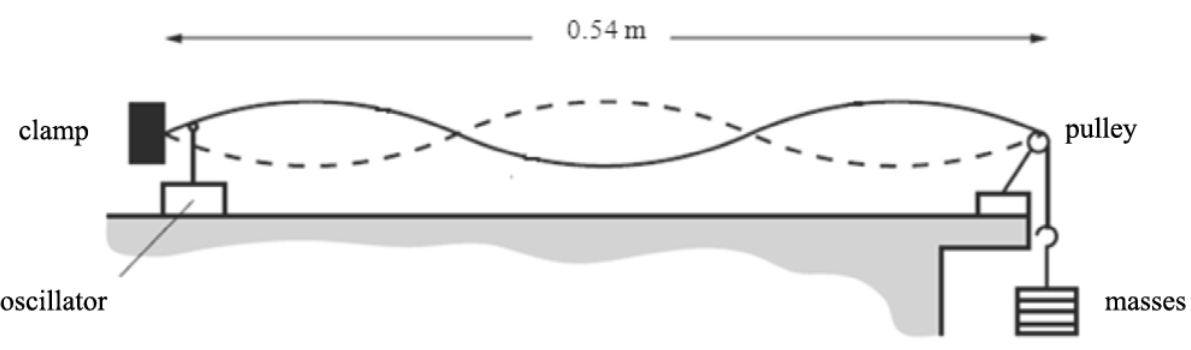
Explain how the stationary wave is formed on the stretched string shown in the diagram

• Waves are reflected at the pulley end.

• This produces nodes and antinodes on the string.

Stationary/ standing wave

• Wave that remains in a constant position with no net transfer of energy

• Characterised by its nodes and antinodes

Node

Point(s) on a stationary wave where the amplitude is always zero

Anti-node

Point(s) on a stationary wave where there is alway the maximum amplitude

2^nd Harmonic in a string (diagram)

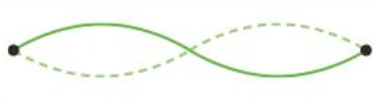
3^rd Harmonic in a string (diagram)

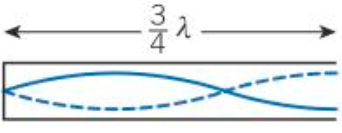
2^nd Harmonic in a air colomn closed at one end (diagram)

There is no 2^nd ___, or any even ____, in an air column closed at one end

3^nd Harmonic in a air colomn closed at one end (diagram)

5^nd Harmonic in a air colomn closed at one end (diagram)

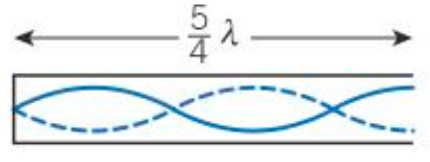
Fundamental frequency

The lowest frequency at which an object (e.g., an air column in a pipe or a string fixed at both ends) can vibrate

Fundamental mode of vibration

A vibration at the fundamental frequency; the first harmonic

Which type of ends do nodes form at on strings?

___ form at fixed ends of a string

Which type of ends do nodes form at in strings?

___ form at closed ends of an air column

Phase difference of points between a pair of nodes

All points between the pair of ___ are in phase

Phase difference of points either side of a node

The points are in anti phase

Phase difference

The difference in degrees/radians between two points on the same wave or similar points on two waves