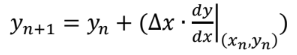AP CALC BC COLD QUIZ

Definition of absolute value

√x^2

Definition of the derivative:

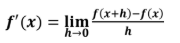
Alternate form of definition of derivative

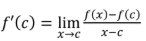
Point slope form of a line

y - y1 = m(x - x1)

Definition of contiunity

1) f(c) is defined

2) limx→c f(x) exists;

3) limx→c f(x) = f(c).

Average Rate of Chage

f(x) AROC = f(b)-f(a)/b-a

Intermediate Value Theorem Conditions

continuous on a closed interval

MVT Conditions & Equation

continuous on [a,b] and differentiable (a,b)

f'(c)=f(b)-f(a)/b-a

Rolles Theorem

f(a)=f(b) -> f'(c)=0

d/dx [c]

0

d/dx [x^n]

nx^n-1

d/dx [f(x)g(x)]

f(x)g′(x) + g(x)f′(x)

d/dx [f(x)/g(x)]

g(x)f'(x)-f(x)g'(x)/g(x)^2

d/dx [f(g(x))]

f'(g(x)) * g'(x)

d/dx sinu

cosu (du/dx)

d/dx cosu

-sinu (du/dx)

d/dx tanu

secu^2(du/dx)

d/dx secu

secutanu(du/dx)

d/dx cotu

-cscu^2(du/dx)

d/dx cscu

-cscucotu(du/dx)

EVT conditions

continuous on [a,b]

Definiton of a Critical Number

f'(c)=0 or undefined

Finding Absolute Max/Min

Candidates Test

f is ___ if x1

increasing

f is ___ if x1f(x2)

decreasing

If f'(x)>0 then f is

increasing

If f'(x)<0 then f is

decreasing

If f'(x)=0 then f is

constant

if f'(x) changes from negative to positive then its a ____ of f

relative minimum

if f'(x) changes from positive to negative then its a ____ of f

relative maximum

f is ___ if f'(x) is increasing

concave up

f is ___ if f'(x) is decreasing

concave down

if f''(x)>0 then f is ___

concave up

if f''(x)<0 then f is ___

concave down

Definition of Inflection Point

f''(c)=0 or DNE

f'' changes between positive and negative

f' changes between increasing and decreasing

if f'(c)=0 and f''(c)>0 then f is ___

relative minimum

if f'(c)=0 and f''(c)<0 then f is ___

relative maximum

(f^-1)'(a)

1/f'(f^-1(a))

if f(g(x))=x then g'(x)

1/f'(g(x))

velocity

s'(t)

speed

|v(t)|

acceleration

v'(t) = s''(t)

displacement

b

∫v(t)dt

a

total distance

b

∫|v(t)dt|

a

speed is increasing when

velocity and acceleration have the same sign

speed is decreasing when

velocity and acceleration have the opposite sign

Left Riemann Sum underapproximates when f(x)

increasing

Left Riemann Sum overapproximates when f(x)

decreasing

Right Riemann Sum underapproximates when f(x)

decreasing

Right Riemann Sum overapproximates when f(x)

increasing

Trapezoidal Riemann Sum underapproximates when f(x)

concave down

Trapezoidal Riemann Sum overapproximates when f(x)

concave up

∫ x^ndx

x^(n+1)/(n+1) + C

∫ sinudu

-cosu + C

∫ cosudu

sinu + C

∫ sec^2(u)du

tanu + C

∫ csc^2(u)du

-cotu + C

∫ sec(u)tan(u)du

secu + C

∫ csc(u)cot(u)du

-cscu + C

b

∫f(x)dx

a

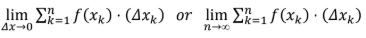
b

∫f'(x)dx

a

f(b)-f(a)

1st FTC

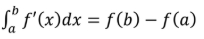
x

d/dx∫f(t)dt

a

f(x)

2nd FTC

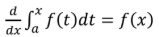
2nd FTC chain rule

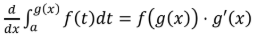
Average Value

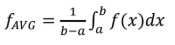
∫1/u du or ∫du/u

ln|u| + C

∫tanu du

-ln|cosu| + c

∫cotu du

ln|sinu| + c

∫secu du

ln|secu + tanu| + C

∫cscu du

-ln|cscu + cotu| + c

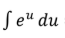
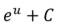
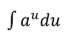
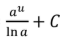
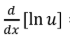
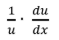
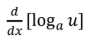
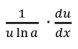
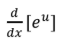
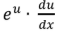
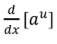
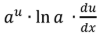
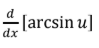
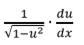
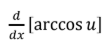
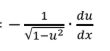
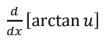
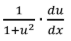
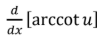
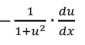
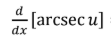
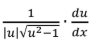
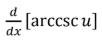
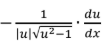
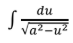
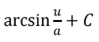
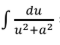
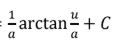
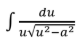
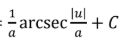
L’Hopital’s Rule

Volume by cross sections

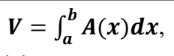
A semi-cricle

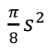
A isosceles w/ leg as base

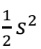
A equilateral triangle

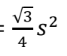
A isosceles w/ hypotenuse as base

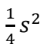
Volume around a horizontal axis by discs

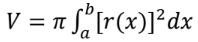
Volume around a horizontal axis by washers

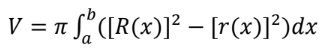
Length of arc for functions

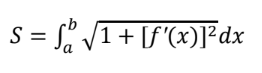
Integration by parts

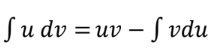
Euler’s Method