Summation
0.0(0)
Studied by 0 people0.0(0)
Call Kai
Learn
Practice Test
Spaced Repetition
Match
Flashcards
Knowt PlayCard Sorting
1/3
There's no tags or description
Looks like no tags are added yet.
Last updated 10:32 PM on 11/21/25
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
4 Terms
1
New cards
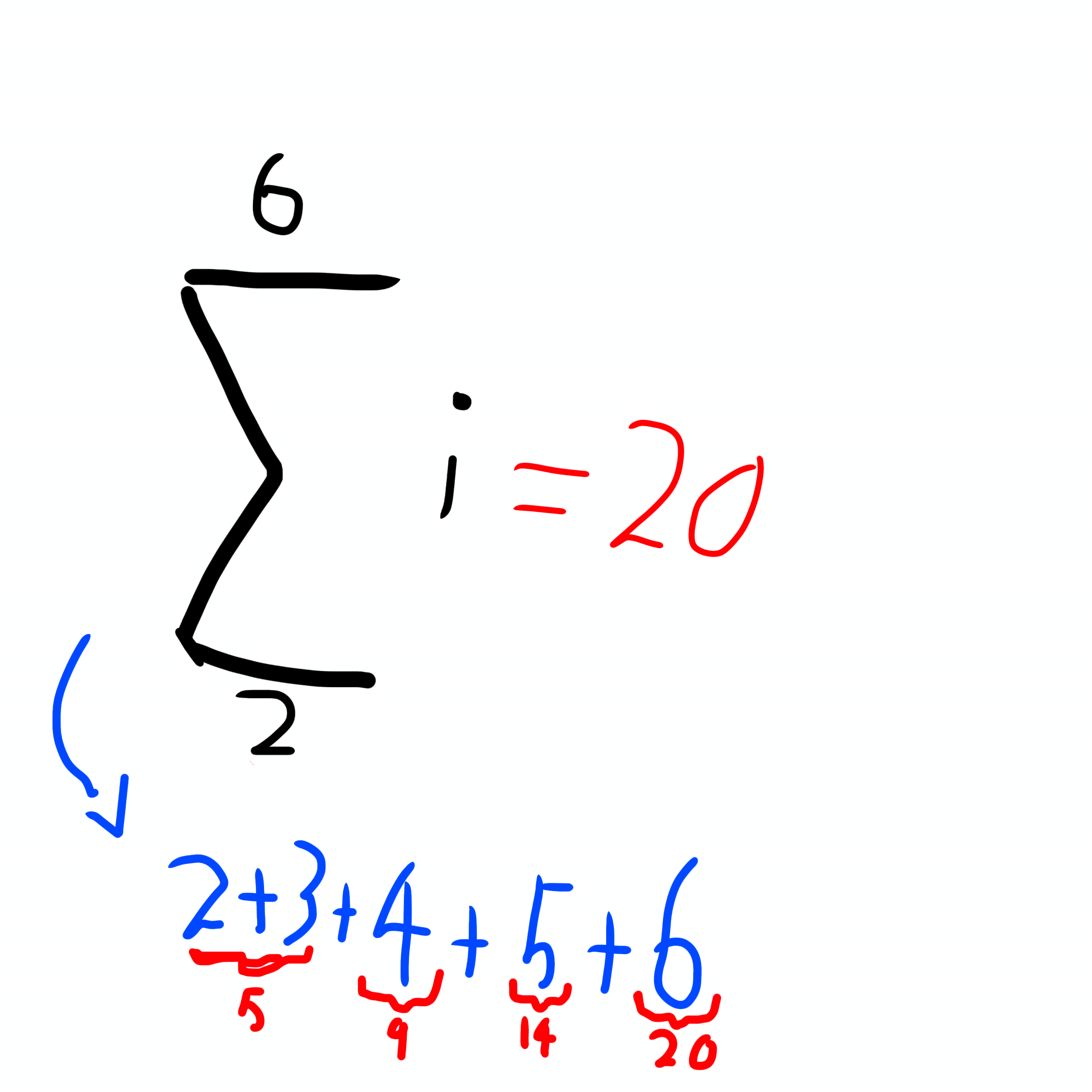
Sigma Notation
when writing a sigma notation, there are three ‘inputs’, the number above (in this case 6), the variable to the left (in this case i), and the number below (in this case 2). what this means is to count from 2 to 6 (so 2, 3, 4, 5, 6) and then add all the numbers up (so 2+3+4+5+6), which equals 20.
2
New cards
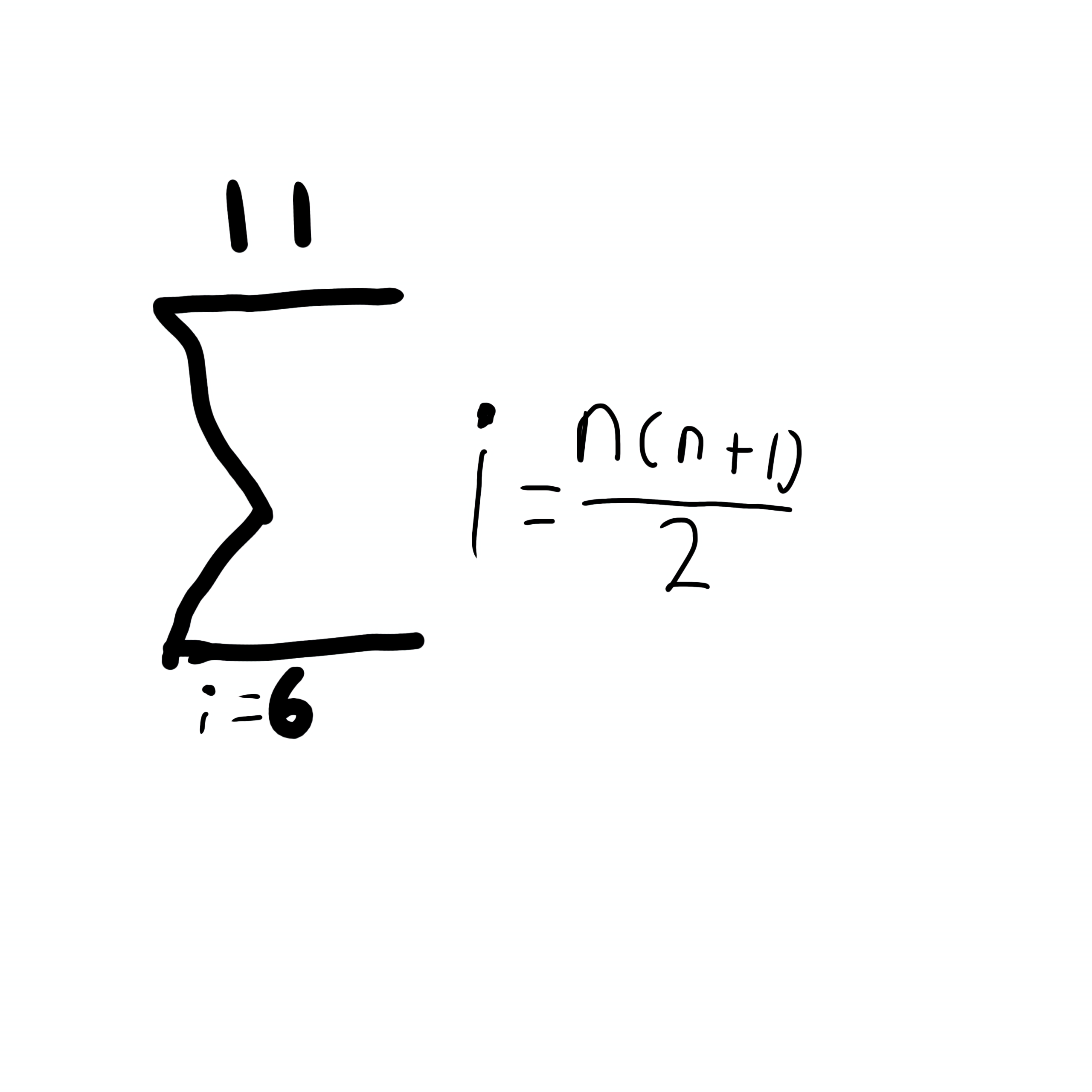
Summation Formulas
to find the answer to a sigma notation, you can use the formula \frac{n\left(n+1\right)}{2} , which basically means “multiply the top number of your notation by itself + 1 (so 11 × 12 for example) and divide by 2" so if n was 11, the answer would be 66
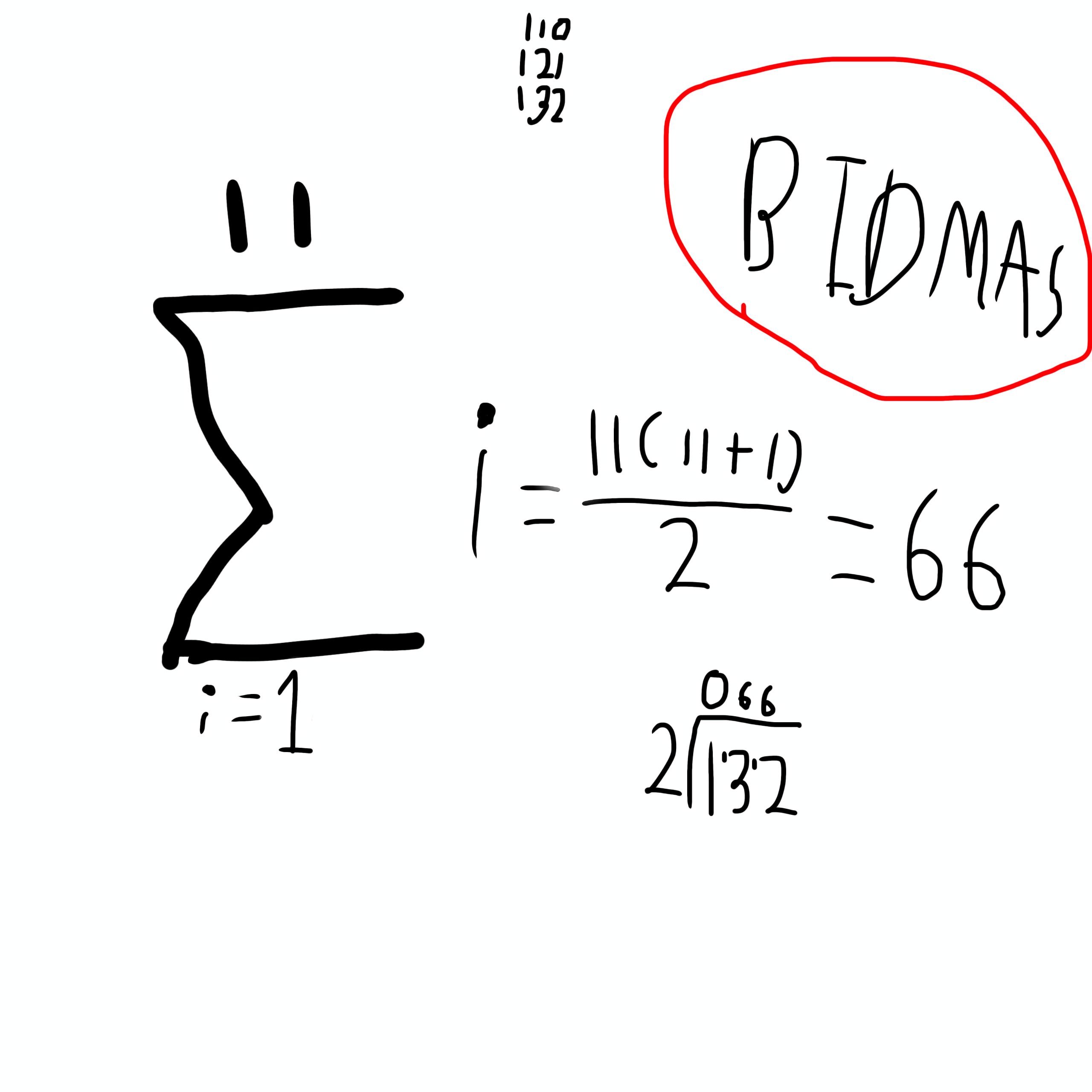
3
New cards
na
na
4
New cards
na
na
Note 
Flashcards (62)