Chapter 18: Confidence Intervals for Proportions

What is a confidence interval?

A range of values, derived from sample data, that is likely to contain the true population parameter.

What is the general form of a confidence interval?

Estimate ± Margin of Error

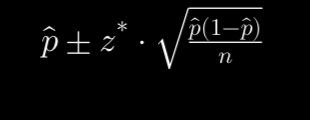
What is the confidence interval formula for a population proportion p?

What conditions must be met to use the confidence interval for proportions?

1. Random sample

2. 10% Condition: sample size ≤ 10% of population

3. Success/Failure: np >= 10 and n(1p) >=10

What does the confidence level represent?

The percentage of all possible samples that would capture the true population parameter.

What happens when you increase the confidence level?

• The margin of error increases

• The interval becomes wider

What happens when you increase the sample size?

• The margin of error decreases

• The interval becomes narrower

What does the margin of error depend on?

• Sample size

• Confidence level

• Sample proportion ^p

What is ≠*?

The critical value corresponding to the desired confidence level (e.g., 1.96 for 95%).

What’s a key misunderstanding about confidence intervals?

Saying “there’s a 95% chance the true parameter is in this interval” — the parameter is fixed, not random.

What happens if conditions aren’t met for inference on proportions?

The Normal model may be invalid; results might be inaccurate or misleading.

Why is the confidence interval centered at ^p?

Because ^p is the best point estimate of the true population proportion p.