Introducing Statistics:

• A proper analysis of data must take into account how the data was collected

• Keep in mind that samples may not be a good representative of the whole population data taken from

• Notice how individuals in the sample are different from all individuals within the population comparatively

Introduction To A Planning Study:

• Identify the population vs. the sample in your study

• A sample is a subset of a population

• Generalizations can only be made if the sample is randomly selected and if the entirety of the sample is taken from the same population

• When evaluating a study, consider confounding variables, outside influences, and the type of study

Types of Studies/Samples:

• Experimental

• Observational

• Randomization

• Matched pairs design

• Blind experiments

• Stratified samples

• Bias samples

• Placebo and control groups

• Simple random samples

Random Sampling and Data Collection:

• Random samples, when well executed, tend to provide a good representation of populations through data (unbiased estimates)

• A simple random sample gives every group of (n) individuals equal chance of being selected

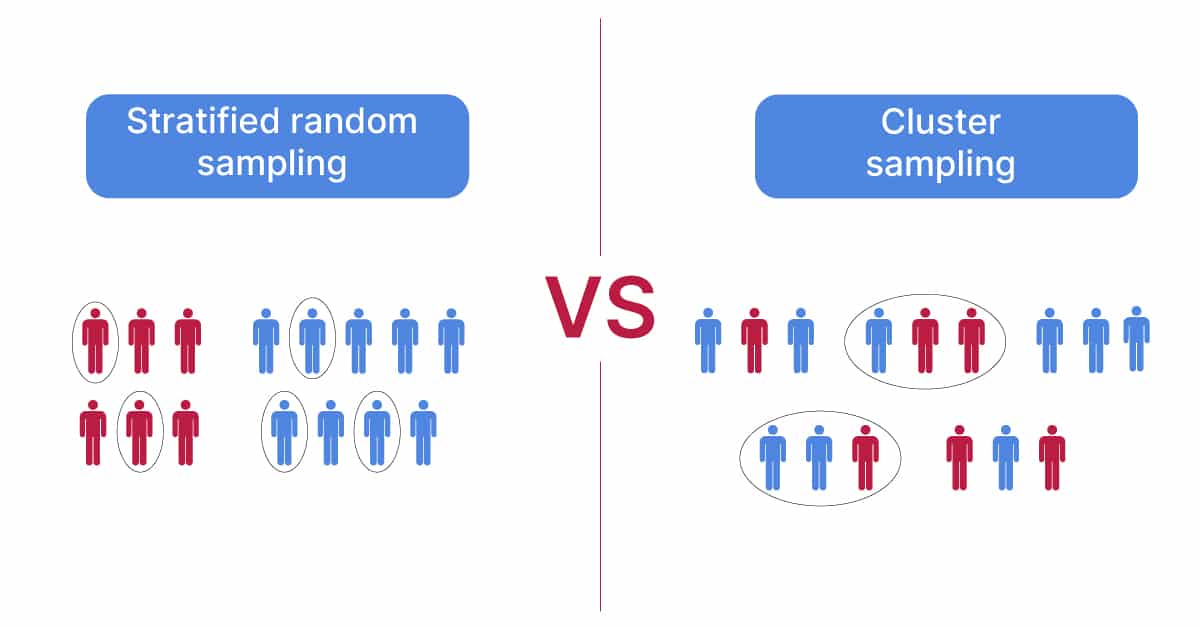
• Cluster sampling creates groups, then randomly samples entire groups (from their group of multiple clusters) (effective when heterogenous)

• Stratified sampling creates groups and then takes random samples from each of those groups (effective when homogenous)

• A voluntary response sample consists of people who choose themselves by responding to a general invitation.

• Choosing individuals from the population who are easy to reach results in a convenience sample.

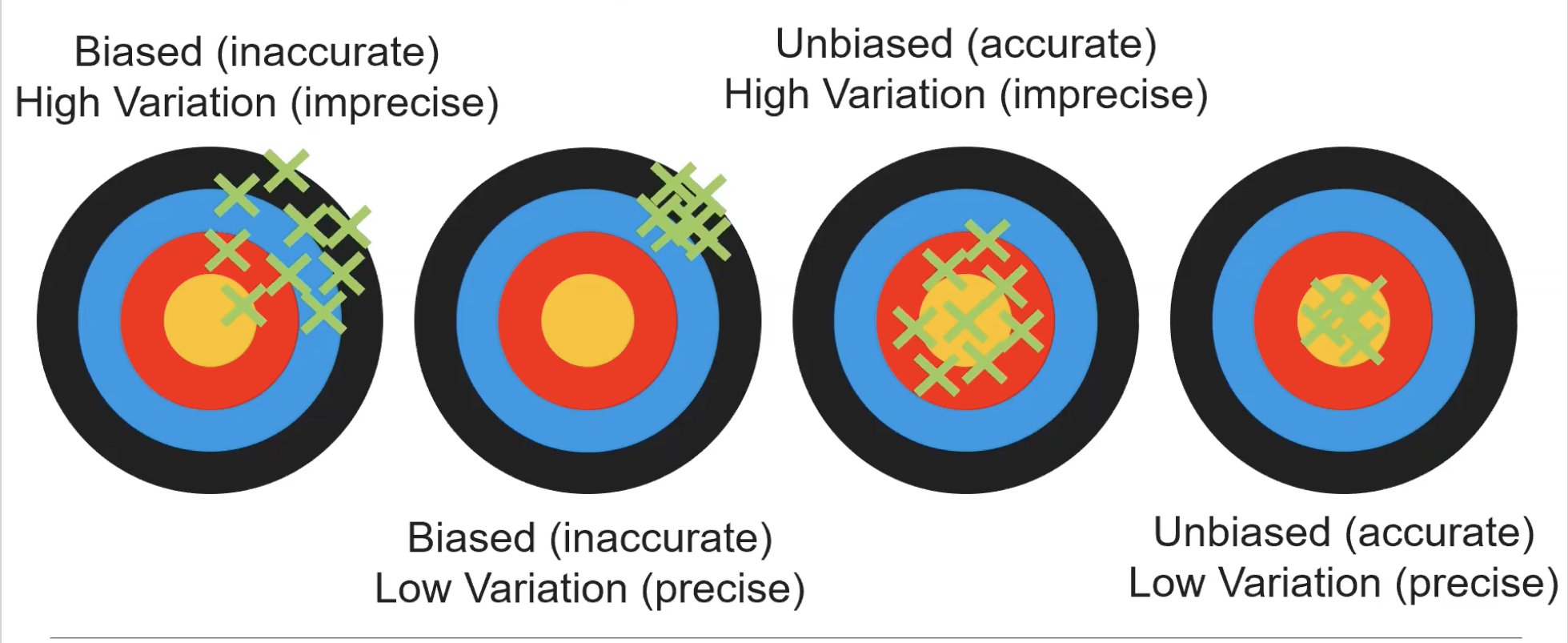
• Low variation provides precise data, while high variation data provides nonprecise data

• Biased samples provide inaccurate data, while unbiased samples provide accurate data

• A census collects data from every individual in the population.

Potential Problems With Sampling:

• Bias arises when certain responses are systematically favored over others

• When explaining a bias, make sure to compare differences between sample and population to highlight contrast

• Also, when explaining bias include if data is over or under-estimated

• Have the reader understand what the sampling method is and why it causes bias

• Undercoverage: occurs when some members of the population cannot be chosen in a sample. 

• Nonresponse: occurs when an individual chosen for the sample can’t be contacted or refuses to participate.

Taking Random Samples:

• Table D (select a line, split numbers in reflection to sample amount, take a sample)

• Use a graphing calculator (Step 1: MATH Step 2: PRB Step 3: randInter(, Step 4: enter)

• Stratified: spilt data into groups of strata, then SRS from each strata to get a sample of a desired amount

• Cluster: split data into groups based on proximity, then randomly select each cluster until the desired sample amount is satisfied

Principles of Experimental Design:

• Comparison: use a design that compares two or more treatments

• Random Assignment: Use the chance to assign experimental units to treatment

• Control: Keep other variables that might affect the response the same for all groups

• Replication: Use enough experimental units in each group so that any differences in treatment groups can be distinguished from chance

Designing Studies:

• Completely randomized design: the experimental units are assigned to the treatments completely by chance

• Double-blind experiment: neither the subjects nor those who interact with them and measure the response variable know which treatment a subject received

• Single-blind experiment: only the researcher knows which treatment the experimental units received

• Observed effect: so large that it would rarely occur by chance is called statistically significant

• A Block: a group of experimental units that are known before the experiment to be similar in some way that is expected to affect the response to the treatments

• Randomized block design: the random assignment of experimental units to treatments is carried out separately within each block

⭐️The main purpose of a control group is to provide a baseline for comparing the effects of the other treatments.