Ionization Constants, Ka and Kb , Determining Ka and Kb Values

16.3-164

Weak Acids and Bases in term of ionization

Incompletely ionized

• Molecules and ions exist in equilibrium

general equation for weak acid and bases

HA = any weak acid; B = any weak base
HA(aq) + H₂O ----> A- (aq) + H3O+ (aq)

B(aq) + H₂O ----> BH+(aq) + OH-(aq)

general equation for weak acids and the acid ionization constant (Ka).
pKa

Acid + Water -------> Conjugate Base + Hydronium Ion
HA(aq) + H₂O ----> A- (aq) + H3O+ (aq)

Ka= [A-] [H3O] / [HA]
pKa = -log[Ka]

general equation for weak base and the base ionization constant (Kb).
pKb

base + Water -------> Conjugate Acid + Hydroxide Ion
B(aq) + H₂O ----> BH+(aq) + OH-(aq)

Kb= Ka= [BH] [OH-] / [B]
pKb= -log [Kb]

Conjugate Acid-Base Pairs and Values of Ka and Kb

1. Consider ionization reaction of generic acid and water

2. Consider reaction of a salt containing anion of this acid (its conjugate base) with water

3. Now adding reactions, we get:
2H2O <=======> H3O+(aq) + OH-(aq)
so, Kb*Ka = [H+][OH] = Kw

So, for any conjugate acid-base pair:

Ka*Kb = Kw = 1.0×10^-14 (at 25 °C)

Using Properties of Logarithms fo the conjugate Acid-Base pairs

Then taking -log of both sides of the equation gives:
-log Ka * -log Kb = -log Kw = - (- 14)

So, from equation, we know that the stronger the conjugate acid, the weaker the conjugate base.

Equilibrium Calculations

Two general types of calculations:

1. Calculating Ka or Kb from initial concentrations of acid or base and measured pH in solution

2. Calculating equilibrium concentrations given Ka or Kb and initial concentrations

1. Calculating Ka and Kb from Initial Concentrations and Equilibrium Data

Need to evaluate mass action expression = reaction quotient Q when the reaction is at equilibrium.
Since Q = K, when at equilibrium (just find the equilibrium),

Can either be given initial concentrations and one equilibrium concentration.
Usually pH orpOH•
OR
can be given initial concentrations and % ionization
% ionization = (moles ionized per liter/ moles available per liter) ×100%

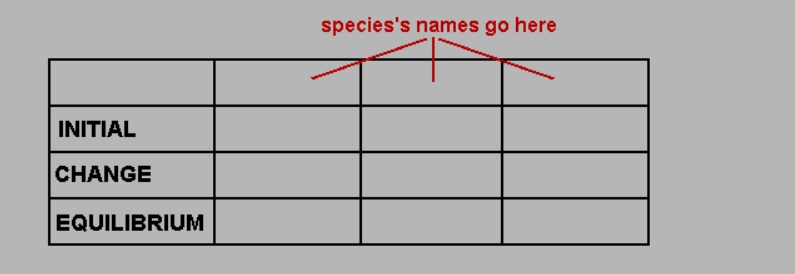
Example 1:
Niotinic acid (niacin) is a monoprotic acid with the formula HC6H4NO2. A solution that is 0.012 M in nicotinic acid has a pH of 3.39 at 25 °C.

What are the acid-ionization constants, Ka, and pKa for this acid at 25 °C?

What is the degree of ionization of nicotinic acid in this solution?

1.1. Write the equation given:
HC6H4NO2 + H2O ------> C6H4NO2 + H3O

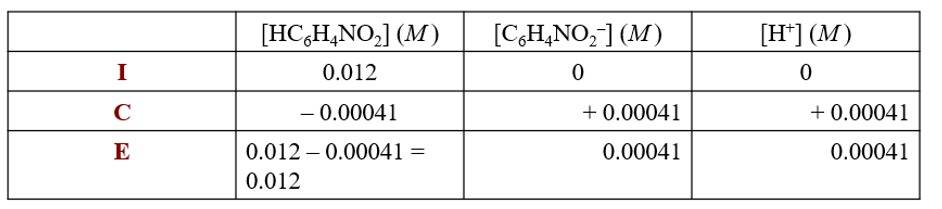
2.1. Make the ICE table

What is the value of x? We know the pH, so we can calculate [H] which is equal to x.

3.39=-log[H]
[H] = 4.1 x 10 ^ - 4

insert the value in the ICE table.

3.1. calculate the Ka,pKa

Ka= [product] / [rectant]
Ka= [0.00041] [0.00041] / 0.012 = 1.4*10^-5

pKa= -log [ 1.4*10^-5] = 4.85

4.1. calculate the the degree of ionization of nicotinic acid in this solution or % ionization

% ionization = (moles ionized per liter/ moles available per liter) ×100%
(0.0004/1 0.012 )x 100% = 3.4%

2. Calculating equilibrium concentrations given Ka or Kb and initial concentrations

Almost any problem where you are given Ka or Kb falls into one of two categories:

1. Only solute is a weak acid

2. Only solute is a weak base