Correlations and linear regression

Describe the uses of correlation analysis 

Correlations = Used to evaluate exploratory data, to evaluate the relationship between two measured variables 

• Measures of correlation ask “what is the relationship between A and B?” or “Does A increase with variable B?” 

• Can be applied to paired observations on two different variables OR applied to one variable measured on two occasions  

Ex: heart rate and level of exertion OR intelligence of a parent and child 

• Pairs of observations (X (independent) and Y (dependent)) are examined to see if they go “together” 

  • Taller people tend to weight more than shorter people 

• Strong correlation = can infer something about the second value by knowing the first  

  • Know how dependent variable is going to behave based on the independent  

• Does NOT equal causation 

  • Could be a 3^rd variable affecting results 

  • Ex: number of churches in a city and crime & random correlation website 

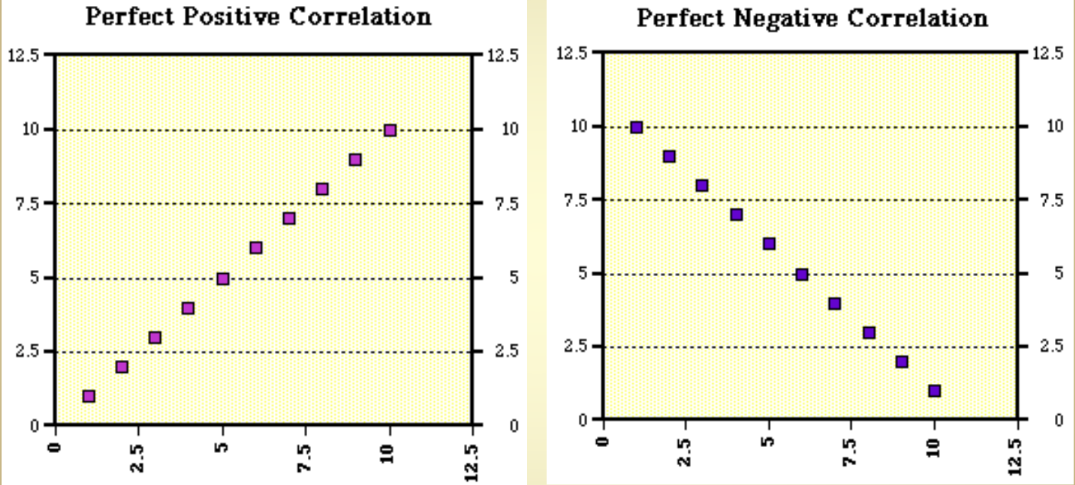
Perfect positive = X increases in the same amount as Y increases 

Perfect negative = X increases in the same amount as Y decreases 

*Can estimate correlation by looking at whether graph is going up/down (positive/negative) or are close or spread apart (1.00 - 0) 

Define the correlation coefficient 

Correlation coefficient (r) = provides an index that is a quantitative measure of the relationship between 2 variables (also known as Pearson’s Product Moment Correlation Coefficient) 

• Ranges from –1.00 to +1.00 

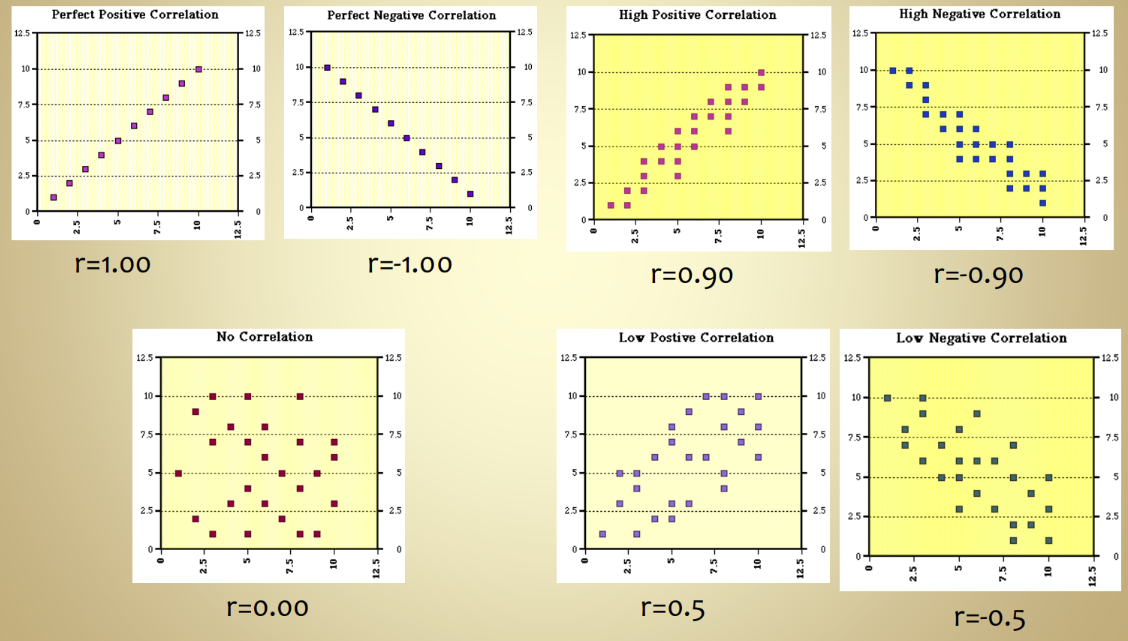
  • Magnitude of the correlation coefficient indicates the STRENGTH 

  • Closer to 1 = STRONGER relationship 

  • Closer to 0 = WEAK relationship (no correlation) 

  • Closer to 0.5 = low correlation 

• Gives the magnitude of a relationship 

  • The sign (+/-) indicates the direction of the relationship 

• Tells you that two sets of data are related in a proportional 

  • DOES NOT PROVIDE INFORMATION RELATIVE TO THE DIFFERENCE BETWEEN SETS OF DATA (just that it’s stat. Diff. From 0) 

  • Use t-test to infer similarities/differences  

• Only works with linear relationships 

Integrate the value of the correlation coefficient with the shape and spread of a scatter plot 

Scatter plots = each point represents the intersection of a pair of related observations 

• Have an X and Y axis 

• The closer the points are to the “straight line” = the higher the correlation (STRONGER RELATIONSHIP) 

• Ranges from –1.00 to +1.00 

• Magnitude of the correlation coefficient indicates the STRENGTH 

  • Closer to 1 = STRONGER relationship 

  • Closer to 0 = WEAK relationship (no correlation) 

  • Closer to 0.5 = low correlation 

• Gives the magnitude of a relationship 

• The sign (+/-) indicates the direction of the relationship 

• Can estimate correlation by looking at whether graph is going up/down (positive/negative) or are close or spread apart (1.00 - 0) 

 

There can be curvilinear relationships  

• Ex: anxiety level and performance 

• Linear correlation will be nearly 0 but the scatterplot will show a clear relationship (curved) 

Differentiate between significance of a correlation and strength of a correlation 

Significance of correlation (p-value) = Indicates that observed correlation is unlikely/likely due to chance 

• Is the correlation coefficient significantly different from 0? 

• Is the observed correlation a random effect or is it a good estimate of the population correlation? 

• DOES NOT mean there is a strong relationship 

  • Can only indicate that it is NOT due to chance at the most 

• Sensitive to sample size 

  • Large sample sizes = r of 0.20 will be considered significant 

  • Small sample sizes = r of 0.45 will be considered significant 

• Less useful in a correlation analysis than the actual magnitude of the correlation 

  • Look more at r value (than p) because all p-value says that it is statistically significant from 0 

• Does not provide information

  relative to the difference between sets of data

Strength of correlation (r ) = tell you that two sets of data are related in a proportional way

Significance DOESN’T tell you anything about the difference between the sets of data

Describe the uses of linear regression analysis 

Linear regression = an inferential procedure that draws conclusions about a population based on samples taken from that population 

• Uses relationship between variables as a basis for prediction 

  • Draws the line of best fit (regression line) 

• Variable X (independent) = predictor variable 

• Variable Y (dependent) = criterion variable 

• Used for correlations less than 1.00 

Interpret the parts of the straight line equation (define outliers and residuals)

Outliers = points that do not seem to fit with the rest of the scores  

• Lies outside the obvious cluster of scores 

• 1 outlier alone can significantly alter the statistical description of the data 

• Don't remove from data UNLESS there’s a good reason 

  • Measurement error 

Linear regression equation: Y = mx + b 

Y = predicted value of Y (dependent variable) 

m = slope (rate of change) 

x = value of independent variable X 

b = Y-intercept (value of Y when X = 0) 

Residuals = degree of error in regression line (residual value = difference between actual Y and predicted Y) 

• Points above/below the regression line (how far away are they from the line of best fit) 

Define the coefficient of determination and compare it to the correlation coefficient 

Coefficient of determination (r^2) = gives the percentage of the total change in Y scores that can be explained by the X scores 

• Measure of proportion 

• Ranges from 0.00 – 1.00 (NO NEGATIVE) 

  • 0 = no correlation 

  • 1 = high correlation 

• The amount of times you can account for Y based on X 

• Ex: 76% of change in blood pressure can be accounted by knowing the age 

  • Therefore, 24% of the time, the change in blood pressure is due to an unknown/unidentified variable 

 correlation coefficient (r ) = measures the strength and direction of the linear relationship between two variables

• CAN BE NEGATIVE

Define “extrapolation” 

Extrapolation = using linear regression to predict Y beyond the range of your data set 

• SHOULD NOT DO THIS ON DATA 

  • Because don’t know where the data will continue to go 

• Using linear regression to predict Y when you know X (“interpolation”) if it’s within the range of your data set (sometimes ok) 

Explain the use of linear regression for a comparison of methods study (what is the comparison method)

Comparison of methods = uses linear regression to evaluate new procedures or equipment in clinical setting  

• Obtain data from both procedures, determine correlation, linear regression line 

  • Old method = X-axis 

  • New method = Y-axis 

• A “perfect” method agreement is: 

  • Y= X 

  • m = 1 

  • b =0 

  • r >0.99 

Define the perfect method agreement for the straight line equation 

Implies that the observed data points perfectly align with the calculated regression line.

A “perfect” method agreement is: 

• Y= X 

• m = 1 

• b =0 

• r >0.99