Probability Distributions Definitions

Continuous random variable

• Has a support that is an interval in the real line.

• E.g., uniform, normal, exponential, Weibull, etc.

• Probability density function 𝑓ሺ𝑥ሻ measures the instantaneous change in the likelihood of 𝑋 having the value of 𝑥

• CDF:

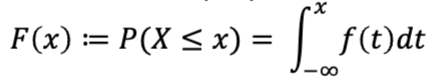
Discrete random variable

• The support is countable (may or may not be finite).

• E.g., Discrete uniform, Poisson, binomial, geometric, etc.

• Probability mass function 𝑓ሺ𝑥ሻ assigns probability to discrete support point 𝑥

• CDF:

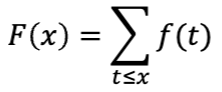
Binomial

the number of successes in 𝑛 trials where each trial is independent from each other with common success probability 𝑝.

Negative binomial

the number of trials required to achieve 𝑟 successes

Geometric is a special case (r=1)

Poisson

the number of independent events that occur in a fixed amount of time and space

Normal

good at approximating the distribution of the sum of a number of random variables

Central Limit Theorem => N(0,1)

Lognormal

good approximation for the product of a number of random variables

Exponential

models time between two independent events; it is the only continuous distribution with the memoryless property.

• If the time between two consecutive events follows exponential, then the number of events in a given interval follows Poisson.

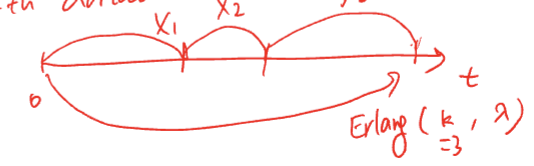
Erlang

the sum of 𝑘 i.i.d. exponential random variables; a special

case of gamma (time until the kth arrival)

Gamma

generalization of Erlang; very flexible at modeling a nonnegative continuous RV

Beta

very flexible at modeling a continuous RV with an interval support; can be a smoother substitute for a triangle distribution

Weibull

models time to failure for components; can model both increasing and decreasing hazard rates

k > 1: increasing hazard rate (time inc more likely to break)

k < 1: decreasing hazard rate (time inc less likely to break)

k = 1: expon(λ) (time inc likeliness to beak stays the same)

At a carpool stand, passengers arrive one by one. When there are three passengers, a driver waiting in the car queue drives up to the stand to pick them up.

How do you model the time between two consecutive pick-ups?

Erlang (3, λ)

At a carpool stand, passengers arrive one by one. When there are three passengers, a driver waiting in the car queue drives up to the stand to pick them up.

Time until the 50th pick-ups?

Erlang (150, λ)

Approx will with N(150/λ, 150/λ²)

The number of absent students in a class of 56?

Binomial (56, p)

p = probability of absence

The number of computer chips we inspect until finding the first defect?

Geom(p)

p = prob of defect

At the customer service hotline, the number of phone calls they receive in the busiest hour?

Poisson (λ * 1)

(rate of arrivals/hr *hr)

The time until the employee fails to perform a task where the longer she works on it, the better she gets (less likely to fail)?

Weibul, k < 1