STV4022

Standardavvik

Det gjennomsnittelige avviket til gjennomsnittet.

Et mål på spredning som som sier noe om graden av variasjon i en enkelt variabel. Standardavviket er på samme skala som variabelen, som gjør den lettere å tolke enn for eksempel variansen.

Standardfeil

Standardavviket til utvalgsfordelingen til en estimator.

Analytisk: standardavvik / kvadratroten av N

Man kan finne standardfeil gjennom simuleringer også, for eksempel gjennom en bootstrapsimulering. Eller gjennom bayesianske simuleringer som stan_glm i R.

Konfidensintervall

Området i utvalgsfordelingen som vi mener mest sannsynlig inneholder den sanne verdien.

Estimator

En estimator kan defineres som en regel for å komme frem til et parameterestimat. For eksempel er gjennomsnittet til et utvalg en estimator for populasjonens gjennomsnitt.

"Vi estimerer for å forsøke å lære om et ukjent populasjons-parameter"


Utvalgsfordelingen til estimatoren = fordelingen av estimater som vi ville fått dersom vi trakk en uendelig mengde utvalg og brukte estimatoren på hvert av dem.

Vi estimerer alltid med mer eller mindre usikkerhet, ettersom vi ikke vet den nøyaktige verdien til populasjons-parameteret. Men vi kan regne ut konfidensintervall for en estimators utvalgsfordeling. Med 95% sikkerhet er populasjons-parameteret to standardavvik pluss/minus fra estimatet.

Normalfordelingen

En kontinuerlig sannsynlighetsfordeling som er formet som en bjelle - kalles ofte "gaussian curve". Nyttig på grunn av sentralgrenseteoremet som sier at modellen nærmer seg en normalfordeling jo større N er.

Gjennomsnitt, median og typetall ligger i midten av fordelingen. Kurven blir bredere jo lenger vekk fra sentraltendensen observasjonene er / jo større standardavviket er. Bred kurve viser altså til mindre presis modell.

Logaritme

Logaritmen er tallet som grunntallet må opphøyes i for å få det aktuelle tallet.

Naturlig logaritme: har grunntall 2.7

Sigma (residual)

Sigma viser til residualenes standardavvik.

Tolkes som et mål på den UFORKLARTE variasjonen i dataene.

Kontinuerlige verdier vs. Kategoriske verdier

Kontinuerlige verdier er nummererte verdier, mens diskrete verdier er kategoriske verdier

Sentraltendens

Gjennomsnitt: sensitiv for uteliggere

Median: mer robust for uteliggere

Modus: observasjonen det er flest av

Populasjonsparameter

Den sanne verdien: for eksempel et gjennomsnitt for hele befolkningen

Hvordan velge riktig estimator?

Man velger den estimatoren som er forventingsrett, effektiv og konsistent

Forventningsrett estimator

Forventningsskjevhet beskriver systematiske skjevheter, målt ved:

Hvor mye gjennomsnittet av utvalgsfordelingen avviker fra den sanne parameteren. Hvis estimatoren er forventningsrett er gjennomsnittet av fordelingen lik den sanne parameteren. Da gjenstår bare eventuelle tilfeldig feil.

En forventingsrett estimator er en estimator som ikke systematisk over- eller underestimerer. Altså at estimatene ikke er skjeve den ene eller andre veien, men er riktig i gjennomsnitt og forventning.

Ettersom vi alltid estimerer med mer eller mindre usikkerhet, vil estimatene alltid differere litt fra den sanne parameterverdien.

Effektiv estimator

En effektiv estimator har en utvalgsfordeling med minst mulig varians / lavt standardavvik.
Varians beskriver spredningen av utvalgsfordelingen, altså:
"hvor store tilfeldige feil medfører estimatoren?"

Effektivitet må sees i sammenheng med forventingsrett estimator, man kan danne en estimator med nærmest ingen varians, men der forventningsskjevheten er høy, noe som ikke er ideelt(feks, dataene ble samlet på en måte som gjorde utvalget skjevt, så nå er fordelingen forventingsskjev, samtidig passer modellen godt med dataene og man har lav varians).
På den andre siden kan en smule med forventningsskjevhet være en ok pris å betale for en stor reduksjon i varians.

Konsistent estimator og Asymptotisk estimator

Egenskaper som er sanne når utvalgsstørrelsen bli stor / uendelig. For et veldig stort utvalg er estimatoren i praksis forventningsrett og effektiv, da mean squared error nærmer seg 0 jo større N man har. Da er estimatoren en konsistent estimator av den sanne verdien

Asymptotisk: sentralgrenseteoremet

Root Mean Squared Error (kvadratisk gjennomsnitt)

RMSE kan brukes til å sammenligne forholdet mellom effektivitet og forventningsretthet for en estimator.

Hvis vi ikke synes den ene typen feilen er verre enn den andre kan vi velge den estimatoren som har lavest RMSE.

Monte Carlo simuleringer

kan brukes for å evaluere asymptotiske kalkuleringe

Alternativ hypotese

Hypotesen med utgangspunkt i mistanken vår

Nullhypotese

Hypotesen som avskriver mistanken vår (den vi forsøker å "nulle" i en frekventisk klassisk hypotesetest)

Type-I feil

Å dømme en uskyldig --> Å forkaste en sann nullhypotese

Signifikansnivået er sannsynlighet for type-I feil

Type-II feil

Å ikke forkaste en usann nullhypotese.

Høyere utvalgsstørrelse typisk reduserer sannsynligheten for type II-feil.

POWER, høy power = mindre sannsynlighet for en type-II feil

Type-M feil (magnitude)

Å overdrive størrelsen på en effekt/sammenheng / når omfanget av en estimert effekt differerer betydelig fra den sanne verdien.

"Statistisk signifikans filteret" øker sjansen for type-M feil, da kravet om signifikante resultater for publisering fører til overestiemrte effekter, ettersom man må ha 2*standardfeil fra estimatet som ikke krysser 0 for å få signifikant resultat. Da vil resultater emd større SE også føre til at man må ha større estimater - uansett hvor ubetydelig sammenhengen egentlig er.

Type-S feil (sign)

Når tegnet til en effekt går motsatt vei av den sanne effekten

Svakheter ved signifikanstesting

Fundamentalt problem med type-1 og 2 feil:

• I mange tilfeller i sv tror vi aldri at nullhypotesen er sann: feks, endring av en lov vil alltid føre til NOE endring, så hypotesen om at loven fører til 0 endring gir ikke mening.

Har egentlig ingen praktisk betydning - Å unnlate å avvise en nullhypotese betyr ikke at vi aksepterer nullhypotesen. avvise en nullhypotese betyr ikke at den alternative hypotesen er riktig da det kan være mange andre alt. forklaringer som egnt er riktige.

Man trenger:

• overbevisende teori

• nye tester

• gjennomgang av alternative forkalrnger

Signifikans

Prosenttall som angir usikkerhet.

Hvis et 95%-konfidensintervall ikke inneholder 0, er estimatet signifikant på 5% nivå i en to-sidig test

Ô + - 2*SE(Ô)

Tosidig hypotesetest

Tester hvorvidt begge sider av en datafordeling er større eller mindre enn fordelingen

Ensidig hypotesetest

Tester hvorvidt estimatoren er større eller midnre enn parameterestimatet

P-hacking

Å leke rundt med signifikanstesting til et gitt nivå er nådd: eks, forskere fant følge Gelman lave p-verder i en medisinsk røntgenundersøkelse av en død laks.

Hvordan unngå dette:

• formulere hypoteser på forhånd

• ,mønstre fra data burde testes på nytt

• analysere all data, ikke kun deler av data

• raportere alle sammenligninger og analyser

• gjøre all data offentlig

Simulering

Spesifisere en sannsynlighetsmodell, og generere data fra modellen.

Til forskjell fra estimering, der modell og data = gir parameterestimater

Hvorfor simulere?

1. Mønstre av tilfeldig variasjon (plott over residualer får frem ikke modellerte mønstre i dataene)

2. Utvalgsfordelingen til data og estimatorene våre (bootstrapping: estimere usikkerhet i estimatene våre, feks får man bootstrappet Standardfeil)

3. Usikkerhet i prediksjoner fra estimerte modeller (posterior_epred for å illustrere usikkerhet i predikerte sannsynligheter i logistisk regresjon)

Byggeblokkene i simulering

• Sannsynlighetsfordeling (normalfordeling eller binomial fordeling)

• Set seed

• Funksjoner

• Subsetting

• If else statements

• Loops

Generere randomisert data

Feks: bruke Bernoulli-fordelingen - eneste parameter er sannsynligheten for suksess (p)

Eksempel R:

bernoulli_simulering

Set seed

R er avhengig av en RANDOM NUMBER GENERATOR for å generere data, rekkefølgen til dataene er bestemt av set seed. Hvis man bruker samme set seed vil man få de samme tallene hver gang hvis du kjører helt identisk simulering for eksempel flere ganger, hvis du der i mot kjører en simulering flere ganger uten å ha satt seed vil du få litt forskjellig output hver gang.

Funksjoner

Funksjoner tar input, gjennomfører en operasjon, og produserer output fra operasjonen.

Loops

Loops repeterer en operasjon for spesifiserte verdier. For eksempel kan man kjøre en loop av tallene 1:10, og den vil printe tallene 1 til 10 på rekke.

If else statements

Kan ofte leses intuitivt

Subsetting

Subsetting betyr å del en porsjon av dataene, som settes i squared brackets.

MAD SD

Kan tolkes som standardfeil, men bruken av median gjør målet mer stabilt. De ganger MAD med 1.483 for å få standardavviket av medianen.

I tolkningen av output fra stan_glm vil median og MAD SD fungere som henholdsvis punktestimat og standardfeil, men de fungerer som mer stabile oppsummeringer av små utvalg eller skjeve utvalgsfordelinger - som gjerne kan oppstå under bruken av logistisk regresjon og GLM.

Bootstrapping (+fordeler og ulemper)

Gir en formening om hvordan datasettet ville sett ut dersom vi kunne ha samlet inn data på nytt.

Bootstrapping er en form for resirkulering av datasett, der man kan anslå usikkerhet i parameterestimatene gjennom å få bootstrappet standardfeil --> særskilt nyttig dersom vi mangler mål på usikkerhet.

Fremgangmåte: Tilfeldig gjenvalg av utvalgets data der utbytting er "lov".

Man lager altså nye datasett - og hver observasjon kan forekomme flere ganger i datasettet, mens noe kan bli utelatt helt.

Komplikasjoner:

• passer dårlig for tidsserie- og flernivådata

• funker dårlig dersom det originale utvalgte var skjevt og var preget av lav validitet (eks: ingen mørke stemte på republikanere, men var bare ikke blitt spurt)

Hva er en regresjonsmodell

En måte å finne den regresjonslinjen som i størst grad beskriver sammenhengen mellom X og Y. Ofte ønsker man også å kontrollere for / holde konstante andre prediktorer.

Kan friste til å trekke kausale slutninger der disse egnt ikke er til stedet.

Man må da tolke outputen til modellen som sammenlikninger av enheter med ulike egenskaper.

Når X øker med en skalaenhet, øker Y med regrksjonskoeffisienten.

Konstantledd

Punktet hvor regresjonslinjen treffer Y-aksen. Verdien for konstantleddet representerer når X = 0

Regresjonskoeffisient

Stigningstallet til regresjonslinjen. Endringen i Y når X stiger med 1 skalenhet.

Tolkning multippel regresjon

Koffa = representerer gjennomsnittlig endring i Y, når det skjer en skalaenhet økning i gjeldende X, mens alle andre X holdes konstante.

F.eks.: 1 representerer den estimerte gjennomsnittlige endringen i Y, per enhets økning i X1 når X2, X3 og X4 holdes konstante.

Konstantledd = representerer Y når alle X-ene er 0.

Har ofte ikke praktisk betydning.
Her kan man ofte sentrere konstantleddet for å oppnå et konstantledd med en mer praktisk tolkning.

Sigma/standardavviket til residualene:
Tolkes som et mål på den UFORKLARTE variasjonen i dataene.

MAD SD:
Samtidig er ikke estimatet til regresjonskoeffisienten statistisk signifikant, ettersom MAD SD er såpass høy sammenlignet med regresjonskoeffisienten, at skalaen vil krysse null. Konfidensintervallet er bredt og inkluderer 0/krysser 0, det er med andre ord stor usikkerhet knyttet til estimatene.

Hva er samspill?

Samspill er når sammenhengen mellom to variabler påvirkes av en tredje variabel.
Feks: stemmeandelen for demokratiske kandidater kan være høyere når inntektene er høye, men kun når presidentenen er demokrat samtidig.

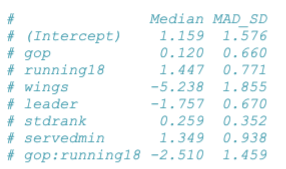
Tolk dette samspillet:
I dette tilfellet vil det si at sammenhengen mellom å være republikaner (gop) og å signere brevet
(filisave), er avhengig av hvorvidt man stiller til valg i 2018 (running18).

variabel*verdi på variabel +- samspillskoeffisient * (verdi på variabel i samspill * verdi på variabel i samspill)

Konstantleddet:
den predikerte verdien når alle uavhengige variabelen har verdien 0. Altså en person som ikke er republikaner (gop=0), og ikke stiller til gjenvalg (run18=0), og også har verdien 0 på alle de andre variablene. Altså vil predikert verdi for en person med 0 på alle variablene være 1.159

Samspillsleddet viser hvor mye hver av sammenhengene endrer seg når vi øker nivået på den andre variabelen i samspillet med én skalaenhet.

Hvis man vil se på sammenhengen mellom gop = 1 og utfallet:

0.120 * (1) - 2.51 *(1 * 0) = 0.120

0.120 (gop=1) – 2.51 *(gop=1*running18=0)

= 0.120


0.120 * (1) - 2.51 *(1 * 1) = 0.120

0.120 * (gop=1) – 2.51 *(gop=1*running18=1)

0.120 - 2.51

= - 2.39

Tilsvarende hvis man vil se på sammenhengen mellom running18 = 1 og utfallet:

1.447 * (1) - 2.51 * (0 * 1)

1.447 * (running18=1) - 2.51 * (gop = 0 * running18=1)

= 1.447


1.447 * (1) - 2.51 * (1 * 1)

1.447 * (running18=1) - 2.51 * (gop = 1 * running18=1)

1.447 - 2.51

= - 1.063

Forutsetninger lineære regresjon

1. Validitet

2. Ytre validitet (representativitet)

3. Additivitet og lineær modell

4. Uavhengige residualer (fravær av autokorrelasjon)

5. Lik varians for residualene (homoskedastisitet)

6. Normalfordelte residualer: (omtrent kun relevant for prediksjon)

Problemet med autokorrelasjon (avhengige residualer)

Dersom residualene korrelerer kan standardfeilen bli overestimert (gir veldig mening hvis du bare tenker litt på det, residualene er jo en slags feilkilde, eller avstanden fra estimert regresjonslinje og observasjonene, så hvis de dobles oppå hverandre gir det større standardfeil), + sannsynligheten for tilfeldige feil i koffa øker.

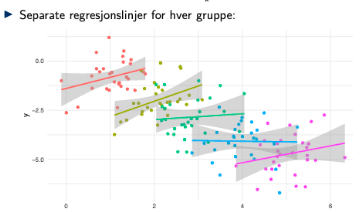
- oppfylles ikke for tidsseriedata, paneldata eller grupperte data (dette kan oppdages ved separate regresjonslinjer for hver gruppe for sistnevnte)

Plot av residualer over predikerte verdier - predict(mod1), resid(mod1)

1. mønsteret er tilfeldig, og ingen residualer skiller seg kraftig ut

2. residualene danner et horisontalt bånd rundt null. Dette tilsier at variansen til residualene er relativt like (aka homoskedastisitet)

Prediktive tester - posterior_predict()
"Posterior predictive tests"

Hvis en modell er en god "fit", burde vi kunne bruke modellen til å generere data som i høy grad ser ut som dataene vi har observert.

Vi bruker modellen til å generere data, for så å sammenligne de nye dataene med faktisk observerte data.

To generate the data used for posterior predictive checks (PPCs) we simulate from the posterior predictive distribution. This is the distribution of the outcome variable implied by a model after using the observed data y (a vector of N outcome values) to update our beliefs about unknown model parameters θ.

Sammenligning, ikke effekt

Multiplikativ vs. additiv

Additiv: En regresjonsmodell antar i utgangspunktet at sammenhenger er additive. Det vil at utfallsvariabelen (Y) kan skrives som en funksjon av typen:
Y = beta1 * X + beta2 * Z.
Additiv refererer her til pluss-tegnet i formelen. X og Z ganges med hver sin koeffisient og legges så sammen.

Multiplikativ: kan f.eks. inkludere et samspill, slik at man får en funksjon av denne typen:
Y = beta1 * X + beta2 * Z + beta3 * X * Z.
Her er X og Z ganget med hverandre i den siste delen av formelen. Det vil f.eks. si at sammenhengen mellom X og Y avhenger av verdiene på Z.

Logtransformering vil gi en slags multiplikativ modell, fordi log(a*b) = log(a) + log(b).

Hvorfor transformere?

1. Forenkle tolkning av modeller F.eks: endre skala, sentrere konstantledd til gjennomsnitt så det blir mer forståelig, standardisering for å enklere kunne sammenligne koeffisienter.

2. Modellere sammenhenger slik at de blir ikke-lineære eller ikke-additive (at prediktorene faktisk interagerer med hverandre).

Sentrering, hvorfor?

Sentrere prediktorene så det blir lettere å tolke konstantleddet, da blir feks konstantleddet gjennomsnittet til prediktoren(e)

Man tar for eksempel: prediktoren minus gjennomsnittet til prediktoren.

Man skifter dermed skalaen, men bevarer enheten - konsekvensen er at regresjonslinjen for prediktoren og utfallet ikke endrer seg, mens tolkningen av konstantleddet endrer seg.

Standardisering, hvorfor?

• Standardiserte koeffisienter reflekterer økninger på ett standardavvik i X

• Standardisering gjør det enklere å sammenligne koeffisienter, fordi man får de på samme skala, nemlig standardavvik.

"Når X øker med ett standardavvik, øker Y med koeffisienten"

⚠️ gir lite mening for binære variabler

Lineære vs. logistiske transformasjoner

Lineære transformasjoner endrer ikke selve sammenhenger vi modellere, kun tolkningen av koeffisientene. Ikke-lineære transformasjoner endrer selve sammenhengen(e) vi modellerer.

Hvorfor logtransformere?

1. Utfall som alltid er større enn 0. Noen typer modeller ignorerer at utfallet for noen variabler alltid er større enn 0. Dersom man gjør en posterior_predictive test vil man gjerne observere at fordelingen til prediksjonene fra modellen ikke samsvarer godt nok med fordelingen på Y. En måte å tilpasse modellen på så den i større grad samsvarer med fordelingen på Y, er å logtransformere Y.

⚠️ ikke like enkelt dersom utfallet også kan være akkurat 0, ettersom log-0 er udefinert, det vil si at en DIREKTE log-transformering av verdien 0 ikke er mulig.

2. Multiplikative sammenhenger (motsatte av additiv). Logtransformering tillater koeffisienter med multiplikativ tolkning. Sammenhengene mellom X og Y er ikke alltid additive, da bryter man i tillegg med en av forutsetningene for lineær regresjon. Dermed kan logtransformering være gunstig.

3. Mer enkelt er logtransformering ofte anbefalt for skjeve data, ettersom logtransformering gjerne har effekten av å spre ut data som har klumpet seg, og på den andre siden samle data som er veldig spredt - for eksempel til kun den ene siden av fordelingen. Det er flere grunner til å ville gjøre dette:

• Det kan bidra til at dataene i større grad likner på en normalfordeling, som kan være gunstig dersom man gjennomfører en statistisk analyse som forutsetter normalitet.

• Det kan bidra til å møte forutsetning om homoskedastisitet -altså at residualene er like på tvers av verdiene - for lineær regresjon

• Det kan også bidra til å gjøre et ikke-lineært forhold, mer lineært.

Tolkning av log Y

Nå er tolkningen på log-skala: feks inntekt og høyde

En skalaenhets/cm økning i x/høyde, korresponderer med en forskjell på koffa i log-inntekt.

Hvis man vil ha utregningen i prosent:

2.7 opphøyd i koeffisienten, minus 1, ganger 100

Tolkning av log X

1 prosent økning i logX korresponderer med en forskjell på koffa skalaenheter for Y.

Tolkning av log X og Y

1 prosent økning i X korresponderer med en forskjell på koffa prosent for Y.

Log-log transformasjoner --> koffa kan tolkes som forventet proporsjonell forskjell i Y, per proporsjonelle forskjell i X - altså prosent mot prosent.

kryssvalidering generelt

Ofte vil vi evaluere og sammenligne modeller uten å måtte vente på nye data - i kryssvalidering bruker man deler av data fra modellen til å predikere, mens en annen del holdes utenfor og behandles som en proxy for fremtidige data.

Dette betyr også at kryssvalidering gjør bukt med problemet med overestimering (overfitting?) som oppstår når man bruker samme data for estimering OG evaluering.

LOO

Kryssvalidering (Leave One Out)

• utelate en observasjon av gangen

• bruke resten av dataene til å predikere den utelatte observasjonen

• gjenta til man har predikert for hver og en utelatt variabel

• bruke elpd til å vurdere hvor godt modellen predikerer

• jo større elpd jo bedre!

Logistisk regresjon, hvorfor?

family = binomial(link = “logit”)

• lineære modeller er kontinuerlig og egner seg ikke bra for binære utfall, den logistiske der i mot passer også for utfall som er mellom 1 og 0.

• det er teknisk mulig å implementere en lineær modell, men den vil da predikere observasjoner større en 1 og mindre enn 0, samt ofte ikke passe god med observasjonene som ikke nødvendigvis tilnærmer seg en rett linje lenger, da vil også forutsetning om homoskedastisitet være brutt ettersom residualene gjerne vil ha rimelig forskjellige størrelser / avstand til regresjonslinjen.

Tolke logistisk regresjon uten predikerte sannsynligheter?

Logistisk regresjon oversetter fra den lineære formen, til sannsynligheten for et utfall.

• Nå er koffa vanskelig å tolke fordi de er på en logit-skala (endringer i log, ikke skalaenhet)

• Koffa vil avhenge av de andre prediktorene

Man kan tolke som odds, altså sannsynligheten for at noe vil skje / sannsynligheten for at noe ikke skjer.

exp(coefficients(logmod1)) #eksponensiering av koffa gir relative forskjeller i odds, men er fortsatt ikke veldig intuitivt og tolke "Når man øker normnetwoods med 1, øker oddsen med 14.5"

Tolke logistisk regresjon som predikerte sannsynligheter

-nå må man tolke i sammenheng med de andre X-ene

-vi må lage scenarier hvor verdiene holdes konstante (for eksempel på median-verdien)

-OG simuleringer for å fange usikkerheten knyttet til prediksjonene

GLM - 5 forutsetninger:

1. Utfallsvariabel Y

2. Prediktorer X, med sine koeffisienter β, som gir oss den lineære prediktoren Xiβ

3. Link-funksjon. Mange forskjellige funksjoner som kobler den lineære X til Y

   (for eksempel: Istedenfor å få de på samme skala som Y/utfallet, får du det på LOGIT-skala).

4. Fordeling: vi predikerer ikke utfallene perfekt, så det vil være noe variasjon rundt punktestimatene predikert av modellen, Y.

5. (av og til har vi andre tilleggs-parametere for å håndtere spesielle problemer som oppstår i noen type modeller)

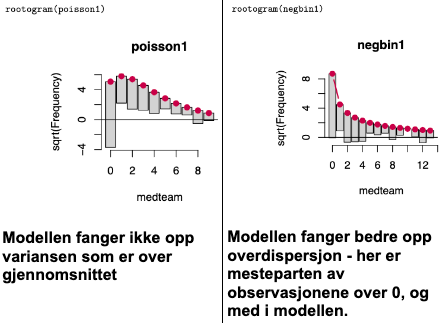
Tellemodeller, Poisson vs. Negativ binomisk modell

- Poisson-modellen antar at variansen i predikert utfall er lik gjennomsnittet
- Ofte er variansen større enn gjennomsnittet, så Poisson er ofte ikke realistisk for statsvitenskapelige data
- Prediksjonene fra poisson-modellen vil i så fall passe dårlig med data


- negative binomiske modeller ligner Poisson, men fanger bedre opp “overdispersjon” (at variansen er større enn gjennomsnittet)

Valg av glm styres av utfall:

POWER, definisjon, og 3 antakelser for gjennomføring

POWER er en designanalyse som kan gjennomføres for å komme frem til sannsynligheten for å få et signifikant resultat, dersom man gjennomfører en potensiell undersøkelse.

Man gjør tre antakelser som danner basisen for simuleringen.

1. Størrelse på sammenhengen (antakelse om hvor stor eller liten en sammenheng er)

2. Signifikansnivå

3. Utvalgsstørrelse

Gelman viser til signifikant funn i 80% av simuleringene som en slags terskel - da basert på hva forskningsinstitutter godkjenner.

NA - hva kan vi gjøre?

ATE og ATT for kausale slutninger

ATE - Average treatment effect

Gjennomsnittsforskjellen mellom de som har fått behandling og de i kontrollgruppe.

ATT - Average treatment effect on the treated

Gjennomsnittsforskjellen for de som har fått behandling

Ignorerbarhet

Gjennom å fordele behandling tilfeldig, sørger man for at de potensielle utfallene er selvstendige fra fordeling av behandling. På denne måten vil den gjennomsnittelige forskjellen i utfall for kontroll- og behandlingsgruppe kunne tilegnes behandlingen. Denne antakelsen kalles formelt for ignorerbarhet.

Gullstandard er eksperiement, for andre forskningsdesign handler det om å finne forskningsdesign som er "as if"-randomiserte.

trusler:
- bakenforliggende variabler, særskilt uobserverte ubakenforliggende variabler, da vi ikke kan kontrollere for disse.

ikke trusler:
mellomliggende variabler, ettersom de kommer etter X, viktig å ikke kontrollere for mellmliggende variabler da dette vil blokkere ut deler av mekanismen som kobler X til Y

SUTVA - stable unit treatment value assumption

De potensielle utfallene til en enhet påvirkes ikke av at andre enheter også får behandlingen.

Denne antakelsen vil for eksempel ikke holde i en undersøkelse om hvorvidt det å rekke opp hånden i forelesning har en positiv effekt på eksamenskarakter, ettersom andre studenter kan lære mer av at studenten stiller spørsmål.

Eksperiment

• den tilfeldige fordelingen av behandling gjør at ignorerbarhetsantakelsen holder i gjennomsnitt

• troverdig at forskjellene vi estimerer ikke påvirkes av bakenforliggende variabler

• vi kan estimere årsakssammenheng mellom X og Y, selv om selvfølgelig masse andre faktorer kan forklare variasjon i utfallene, og feks økologisk validitet kan være et problem for generalisering, vil vi fortsatt kunne estimere den direkte årsakssammenhengen mellom X og Y.

Regresjon vs. matching for ignorerbarhetantakelsen

Felles problem for matching og regresjon:

Kan ikke kontrollere for uobserverbare bakenforliggende variabler - uten et veldig sterkt forskningsdesign vil det dermed alltid være sannsynlig at man har utelatt variabler som bidrar til å forklare variasjonen i en sammenheng i større eller mindre grad.

Vi inkluderer de bakenforliggende variablene i regresjonsmodellen


Regresjon:
Vi vet kanskje ikke hvilken transformasjon av X vi skal velge, eller om vi skal ha interaksjoner mellom de ulike kontrollvariablene

På deler av fordelingen for X finnes det kanskje ikke enheter med begge verdiene vi er ute etter, f eks både D = 1 og D = 0.

Resultatene våre kan avhenge av tilfeldige valg om hvordan vi spesifiserte modellen.


Matching:
For hver enhet med feks D = 1, finner vi en enhet med D = 0 som er mest mulig lik på X, for så å matche disse.

Enheter som ikke har en “match” fjernes fra datasettet.

Reduserer problemet tilknyttet vilkårlige valg når vi spesifiiserer regresjonsmodellene,

Problemer:
MEN vi vil miste en del observasjoner dersom det er mange observasjoner som ikke har en match.

Hva bestemmer om en modell er en dårlig "fit"

En modell som er en dårlig fit har gjerne uvanlig store residualer eller spredningsmål, altså når det er stor forskjell mellom modellens predikerte verdier fra dataene og observerte verdier fra dataene. Dersom observasjonene differerer kraftig fra modellen, feks regresjonslinjen, er det en dårlig fit.

Sigma:

den sier noe om hvor mye uforklart variasjon det er rundt regresjonslinjen

Det er ofte begrenset hva man kan lese ut av disse verdiene, men man kan eventuelt sammenligne dem med standardavviket for de observerte verdiene på utfallsvariabelen: Om sigma er mye lavere, tilsier det at modellen forklarer/predikerer en betydelig del av variasjonen i dataene.