Exam 1 - Chemistry

Classify matter into types based on compositions (Chapter 1 - OB)

Recognize different types of properties and use these properties to help identify substances (Chapter 1 - OB)

Differentiate between physical & chemical changes (Chapter 1 - OB)

Explain the difference between matter, mass, and weight (Chapter 1 - OB)

Differentiate between hypothesis, theories, & laws (Chapter 1 - OB)

Recognize measurement systems and types (Chapter 1 - OB)

Determine the number of sig figs in a number or measurement (Chapter 1 - OB)

Round to the correct number of sig figs after a calculation (Chapter 1 - OB)

Write equivalencies between metric units using the numerical values of prefixes (Chapter 1 - OB)

Write conversion factors between metric units, metric & U.S. units, from context, and from percents (Chapter 1 - OB)

Types of Matter (Chapter 1)

Matter is anything that occupies space (has volume) and has mass, includes particles

2 types:

• Pure Substance

  • Element

  • Compound

• Mixture

  • Homogenous

  • Heterogenous

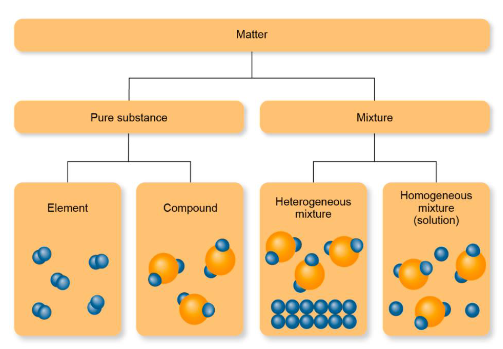
Type of Matter: Pure Substance (Chapter 1)

Element: made of a single type of atom, existing in its natural state

• Example: copper

Compound: made of more than one type of atom (element)

• Example: copper(II) chloride

Types of Matter: Mixture (Chapter 1)

Made of more than one substance, physically combined, sitting together

• Homogenous mixture

• Heterogeneous mixture

Types of mixtures: Homogenous mixture (Chapter 1)

Uniform in composition, cannot see the different components (molecules)

• Example: broth

Types of mixtures: Heterogeneous mixture (Chapter 1)

Not uniform in composition, can see the different components

• Example: stew

Substance Matter - Practice (Chapter 1)

• Salt

• M&M’s

• Food coloring

• Caffeine Molecule

• Aluminum Can

• Coffee

• Compound

• Heterogeneous mixture

• Homogeneous mixture

• Compound

• Element

• Homogeneous mixture

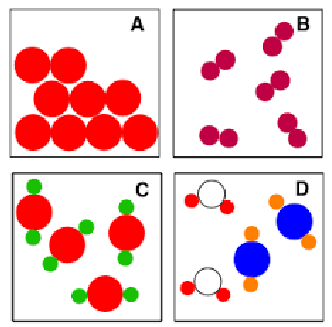
Particle Diagrams (Chapter 1)

• A

• B

• C

• D

• Element

• Element (diatomic)

• Compound

• Mixture (likely heterogeneous)

Types of Properties (Chapter 1)

• Intensive

• Extensive

Types of Properties: Intensive (Chapter 1)

Amount doesn’t matter, is a property of the substance no matter the size of the sample (part of the substance)

• Luster (shine), density

Types of Properties: Extensive (Chapter 1)

Amount matters, size of the sample dictates property, measurements matters

• Carat, mass

Properties Practice (Chapter 1)

• Size

• Density

• Flammability

• Boiling point

• Extensive

• Intensive

• Intensive

• Intensive

Types of Properties & Changes: Physical (Chapter 1)

Properties: Characteristics that can be observed without changing the identity of the substance

• Bread dough is pale in color, has a squishy texture, smells of flour

Changes: changes that alter the appearance of substance, but not its identity, process (Melting, Dissolving)

• Rolling or flattening changes shape

• Solid, Liquid, Gas

Types of Properties & Changes: Chemical (Chapter 1)

Properties: Characteristics (reaction) that describe the ability of a subtense to change into a different substance

• Bread dough is sensitive to heat

Changes: Changes that alter the identity of a substance, giving it new physical and chemical properties (React)

• Baking turns dough into bread, outside becomes brown and crusty

• Makes compounds from different types of elements

Practice: Chemical or Physical Properties / Changes (Chapter 1)

Properties:

• Yellow

• Reacts with acid

• Boils at 100°C

Change:

• Burning

• Melting

• Dissolving

Properties:

• Physical

• Chemical

• Physical

Change:

• Chemical

• Physical

• Physical

Mass (Chapter 1)

Amount of matter

(Measured as weight)

Metric Unit: gram (g)

SI unit: kilogram (kg)

Weight (Chapter 1)

Force of gravity acting on matter

• Measured same, but weight would be different on other planets/the Moon

Parts of the Scientific Method Practice- Observation, hypothesis, experiment, or conclusion (Chapter 1)

a. My sunflower grows best with moderate watering

b. My sunflower is not growing

c. My sunflower needs more water to grow

d. I am going to water my sunflower every other day

a. Conclusion

b. Observation

c. Hypothesis

d. Experiment

Hypotheses (Chapter 1)

Untested ideas based on observations

• When metal gains weight as it turns to a powder, air is added to it

Theory (Chapter 1)

Explanation for something based on many experiments by many scientists that has been accepted by the scientific community

• Oxygen theory of combustion: when metals burn in oxygen from the air combines with the metal to make a new substance

Law (Chapter 1)

Statement about something that is upheld consistently

• Law of conservation of mass: matter cannot be created nor destroyed

Metric System (Chapter 1)

• Used in science, health professions, most other countries, has values based on powers of 10

• International system of units (SI): official system of measurement used throughout the world

• Both systems used in chemistry, depending on context

Volume (Chapter 1)

The amount of space a substance takes up

Metric unit:

• Liter (L)

SI unit:

• cubic meter (m³)

Length (Chapter 1)

How long an object is

Metric & SI unit:

Meter (m)

Temperature (Chapter 1)

How hot an object is

Metric unit:

• degrees Celsius (°C)

SI unit:

• Kelvin (K)

Time (Chapter 1)

How long it takes for something to occur

Metric & SI unit:

• seconds (s)

Taking Measurements (Chapter 1)

Measurements can only be as precise as the device the measurements came from

• Identify the smallest increment marked on the device

• Estimate one place past markings

Precision (Chapter 1)

Repeatability or how finely a device measures

How close the data is to aeach other

Accuracy (Chapter 1)

How close to correct (to true value)

Sigficant Figures Rules (Chapter 1)

Any zeros to the left of all nonzero are not significant

Ancy zeros between significant digits are significant

Any zeros to the right of all nonzero digits in a number with decimal places are significant

Any zeros to the right of all nonzero digits in an integer are uncertain, but assume are not significant if no further information

All digits in the coefficient of a number in scientific notation are significant

Sig. Figs. Practice (Chapter 1)

• 2056.0

• 0.000193

• 1860

• 5

• 3

• 3

Rounding with S.F. (Chapter 1)

Determine how many s.f. are allowed, look at digit just past the last allowed digit — if greater than or equal to 5, if less than 5, round down

Rounding with S.F. Practice (Chapter 1)

• Round to 2 s.f.: 2060

• Round to 3 s.f.: 0.0102549

• Round to 2 s.f.: 100

• Round to 3 s.f.: 2193.5

• Round to 1 s.f.: 0.000356

• 2100

• 0.0103

• 1.0 × 10³

• 2193.5

• 0.0004

Adding/Subtracting S.F. (Chapter 1)

Look for least number of decimal places (least precise) value — this is number of decimal places the answer can have

Adding/Subtracting S.F. Practice (Chapter 1)

• 1.234 + 4.1 =

• 78 - 42.6 =

• 107.2 + 6.58 =

• 99 - 37.1 =

• 5.3

• 35 (no decimal places)

• 113.8

• 62 (no decimal places)

Multiplying/Dividing S.F. (Chapter 1)

Look for least number of s.f. — this is number of s.f. the answer can have

Multiplying/Dividing S.F. Practice (Chapter 1)

• 1500 × 2.63 =

• 0.153/0.006102 =

• 218 × 0.003 =

• 4.7 × 10⁶ / 952=

• 3900 (2 s.f.)

• 25.1 (3 s.f.)

• 0.7 (1 s.f.)

• 4900 (2 s.f.)

2-Step Math with S.F. Practice (Chapter 1):

• Determine how many centimeters are in 8.4 inches.

• Determine how many meters the value above represents

• 8.4 in. x 2.54 cm/1 in. = 21.336 → 21.3 cm (should be 2 s.f., keep 3 for now)

• 21.3 cm x 1 m/100 cm = 0.21 m (round to correct s.f. based on numbers provided — 2 s.f.)

2 - Step Math with S.F. Practice Part 2 (Chapter 1)

• (482 - 15.4)/26

• (0.021 + 0.95)(1.2)

• 17.61/(2.4 - 0.81)

• 482 - 15.4 = 467

  • 467/26 = 18 (2 s.f.)

• 0.021 + 0.95 = 0.97

  • 0.97 × 1.2 = 1.2 (2 s.f.)

• 2.4 - 0.81 = 1.6

  • 17.61/1.6 = 11 (2 s.f.)

Metric Units (Chapter 1)

• A base unit represents a type of measurement such as length or mass

• A prefix is part of the name of a metric unit that precedes the base unit and specifies the size of the measurement

• We can place a prefix in front of any metric unit to increase or decrease its size by some factor of 10

• The relationship of prefix to unit is expressed by replacing the prefix with its numeral value, ex. kilo = 1000, 1 kilometer = 1000 m

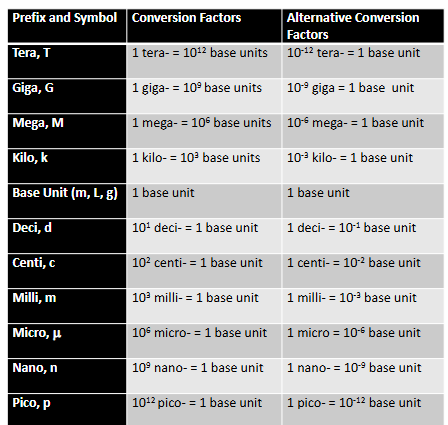
Metric Equivalencies Practice (Chapter 1)

• 1 L = ? mL

• 1 g = ? ng

• 1 um = ? m

• 1 g = ? kg

• 1000 mL or 10³

• 1 × 10⁹ ng

• 1 × 10^-6 m

• 1 × 10^-3 kg

Conversion Factors (Chapter 1)

A fraction that shows an equivalency between 2 units

• Values from the metric system are exact numbers — don’t count towards sig. figs.

• “Per” means fraction bar

• A percent can be written as a conversion factor out of 100 total objects

Examples:

• 1000 g/1 kg or 1 kg/1000 g

• 10 × 10^-9 L/1 nL or 1 L/1 × 10^-9 nL or 1 L/1 × 10⁹ nL or 1 ×10⁹ nL or 1 L

• 14% of the paperclips were purple:

  • 14 purple paperclips/100 paperclips

Special volume equivalency: 1 cm³ = 1 mL

• 1 cm³/1 mL or 1 mL/1 cm³

Conversion Factors Practice (Chapter 1)

Write 2 conversion factors for the relationship between each set of units

• Grams and milligrams

• Liter and deciliters

• Meters and gigameters

• 18% of the pens were blue

• 1 g = 1000 mg or 0.001g = 1 mg

  • 1 g/1000 mg or 1000 mg/1 g or 0.001 g/1 mg or 1 mg/0.001g

• 1 L = 10 dL or 0.1 L = 1 dL

  • 1 L/1 dL or 10 dL/1 L or 0.1 L/1 dL or 1 dL/0.1 L

• 1 Gm = 1 × 10⁹ m or 1 × 10^-9 Gm = 1 m

  • 1 Gm/ 1 × 10⁹ m or 1 × 10⁹ m/1 m or 1 × 10^-9 Gm/1 m or 1 m/1 × 10^-9 Gm

• 18 blue pens/100 pens

Unit Conversions Practice Part 2 (Chapter 1)

• How many inches are in 72.4 feet? (1 ft = 12 in.)

• How many cups is 0.0125 gallons? (1 Gallon = 4 quarts, 8 pints, 16 cups)

• 72.4 ft x 12 in/1 ft = 869 in

• 0.0125 gal x 16 cups/1 gal = 0.200 cups

Metric Unit Conversion Practice Part 3 (Chapter 1)

• How many nanometers are in 5.3 m?

• The volume of a liquid is 250 uL. What portion of a gigaliter is this?

• The mass of an object is 25.61 g. How many mg is this?

• How many megameters are represented by 450 cm?

• 5.3 m x 10⁹ nm/1 m = 5.3 × 10⁹ nm

• 250 uL x 1 L/10⁶ uL x 1 GL/10⁹ L = 2.5 × 10^-13 GL

• 450 × 1 m/100 cm x 1Mm/10^-6 Mm

Mixed Unit Conversions Practice (Chapter 1)

• If you drive 13.27 miles, how many centimeters have you traveled? (1 in = 2.54 cm, 1 mi = 5280 ft)

• An object is measured to have a mass of 126.4 g. How many pounds is this? (1 lb = 0.4536 kg)

• 13.27 mi x 5280 ft/1 mi x 12 in/1 ft x 2.54 cm/1 in = 2.136 × 10⁶ cm

• 126.4 g x 1 kg/1000 g x 1 lb/0.4536 kg = 0.2787 lb

Compounds Units Practice (Chapter 1)

• A boat travels at 45 miles per hour. What is this speed in km/min? (1 mi = 1.609 km)

• You buy some candy that costs 55 cents per pound. What is the price of the candy in dollars per kilogram? (1 lb = 0.4536 kg)

• 45 mi/1 h x 1.609 km/1 mi x 1 h/60 min = 1.2 km/min

• 55 cents/1 lb x 1 lb/0.4536 kg x 1 dollar/100 cents = 1.2 dollars/kg

Squared or Cubed Units (Chapter 1)

When a conversion factor has to be squared or cubed, both the numbers and units in the numerator and denominator must be squared or cubed

A useful conversion factor 1 mL = 1 cm³

Squared or Cubed Units Practice (Chapter 1)

• A volume is measured as 1.625 L. What is this volume in m³?

• A unit pressure is pounds per square inch (psi). How much is 34.1 psi in g/cm²? (1 lb = 0.4536 kg, 1 in = 2.54 cm)

• The density of aluminum is 2.7 g/cm³. What is this density in dg/L?

• The volume of a cube is determined to be 46.2 mm³. What is this volume in uL?

• 1.625 L x 1000 mL/1 L x 1 cm³/1 mL x (1 m/100 cm)³ = 0.001625 m³

• 34.1 lb/1 in² x 0.4536 kg/1 lb x 1000 g/1 kg x (1 in/2.54 cm)² = 2.40 × 10³ g/cm²

• 2.7 g/1 cm³ x 10 dg/1 g x 1 cm³/1 mL x 1000 mL/1 L = 27000 dg/L

• 46.2 mm³ x (1 cm/10 mm)³ x 1 mL/1 cm³ x 1 L/1000 mL x 10⁶ uL/1 L = 46.2 uL

Density (Chapter 1)

= mass/volume or d = m/V

Always the same for a given pure substance

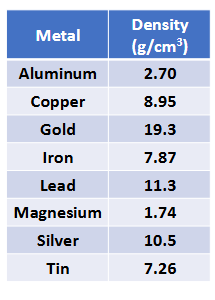
Density Practice (Chapter 1)

• Calculate the volume of a sample of aluminum with a mass of 13.7 g.

• 3.58 L of an unknown substance has a density of 7.87 kg/L. Find the mass of the sample. Identify the substance (1 kg/L = 1 g/mL)

• The mass of an unknown substance is 84.9 g and it takes up a volume of 1.169 × 10^-5 m³. Identify the substance.

• 270 = 13.7/V → 2.70V = 13.7 → V = 13.7/2.70 = 5.07 cm³

• 7.87 = m/3.58 → 7.87 × 3.58 = 28.2 kg Iron

• 84.9 g/1.169 × 10^-5 m³ x (1 m/100 cm)³ = 7.26 g/cm³ Tin

Temperature Formulas (Chapter 1)

T_c = 5/9 (T_F -32)

T_F = 9/5 T_C +32

T_K = T_C + 273.15

Temperature Practice (Chapter 1)

• Convert 195°F to °C (T_c = 5/9 (T_F -32))

• A liquid is measured to be 14.9°C, what is this temperature in kelvin? (T_K = T_C + 273.15)

• What is 402 K in °F? (T_F = 9/5 T_C +32)

• 90.6°C

• 288.1 K

• 264°F