Mechanical waves

Mechanical wave

A spreading disturbance (forced displacement of particles) in elastic medium- MW transfers energy but not mass

MW may take a form of an elastic deformation in solids or a variation of pressure in gases

What is sound?

Any MW/mechanical vibration producing hearing perception

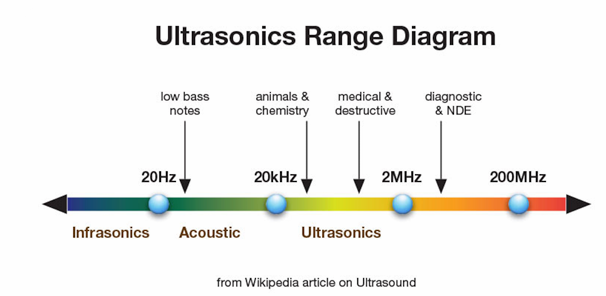
Acoustic spectrum, freq ranges

Infrasound → MW with frequency below 20Hz

Acoustic range → 20Hz - 20kHz

Ultrasound → High frequency above 20kHz

When can sound propagation occur? NB!

In elastic media only. The vibrations in elastic matter are transmitted consecutively from particle to particle causing recurrent alteration of density

Physical characteristics of sound (6):

• Sound intensity (I)

• Sound pressure (P)

• Sound frequency (f)

• Sound velocity (SV)

• Sound wavelength (λ)

• Acoustic impedance

1. Sound intensity (I)

The average sound energy transmitted per sec through unit area, perpendicular to the direction of sound propagation.

It quantifies the loudness of a sound at a given location.

Sound intensity : I = E/t.s

I - sound intensity (W/m²)

E - energy transferred by sound wave, joules (J)

t - time over which energy is transferred, seconds (s)

s - surface area through which sound wave passes (m²)

2. Sound pressure (P)

The sound force (N) acting on the surface area (m²) perpendicular to the sound direction

Sound pressure : p = Δpsin(φ)

p - instantaneous sound pressure at a particular point in the space at a given time, pascals (Pa)

Δp - peak sound pressure (maximum pressure), pascals (Pa)

sin(φ) - phase angle of the sound wave at a given point in space and time

How to calculate peak sound pressure (Δp)

If you know the sound intensity (I) :

I = Δp² / 2ρc Rearrange → Δp = √2Iρc I - sound intensity, W/m² Δp - peak sound pressure, Pa ρ - density of medium (kg/m³) c - speed of sound in medium (m/s)

If you know particle velocity (v) :

Δp = ρcv

v - peak particle velocity (m/s)

From the acoustic impedance :

Δp=zv

z = acoustic impedance (Pa·s/m) v = peak particle velocity (m/s)

3. Sound frequency (f)

Number of vibration per sec, measured in Hertz (Hz) Sound depends on physical properties of medium (density, temp, elasticity etc.) NOT on the frequency

Quantity related to f is the period - T = (1/f)

4. Sound velocity (v)

Quantity which depends on the properties of the medium through which sound propagates, dependent on the elastic properties and density of the medium

5. Sound wavelength (λ)

Distance between two consecutive sound fronts, measured in metres

Wavelength (λ)= Wave velocity (v) ⋅ Time period (t)

Wavelength (λ)= Wave velocity (v) / Frequency (f)

λ - meters (m) v - m/s t - seconds (s) f - Hertz (Hz)

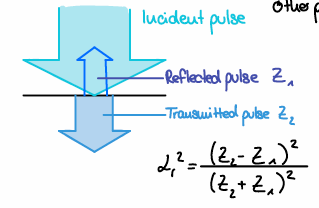
6. Acoustic impedance (z)

Sound propagation through a certain medium is determined from z, when sound wave encounters a border between two different media - one part of wave reflects, the other part passes due to differences in acoustic impedances Z1 & Z2.

Acoustic impedance (z) = p (density of medium) x v (sound velocity)

Two types of sound

Complex & simple tone

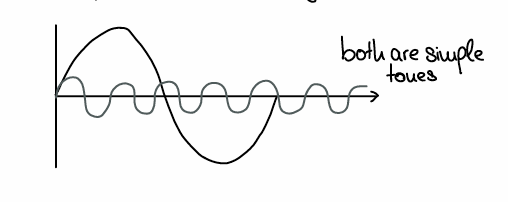
Simple tones

a.k.a pure tone - sound wave with a single frequency.

Vibration should have a sine wave & possesses a certain frequency.

Contains no overtones or harmonics

Examples : electronically generated beep

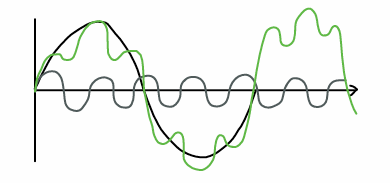
Complex tones

Consists of multiple frequencies, several simple tones.

Waveform appears jagged/irregular

Examples : human voice, musical instrument

Psychophysical characteristics (5)

These are subjective, they are measurements of sounds perceived by the human ear.

1. Sound intensity level E

2. Audibility area

3. Sound pitch

4. Timbre

5. Loudness level

Sound intensity level (E)

Logarithmic measure of the intensity of sound relative to a reference intensity.

Measure in decibels (dB), E is defined at 1000Hz sound frequency only.

E = k(10) ⋅ log₁₀​(I/I₀​)

• E - sound intensity level, dB

• k - coefficient, bel = 1, dB = 10

• I - sound intensity, W/m²

• I₀ - threshold of hearing, 10^-12 W/m²

Loudness of sound (L)

Quantity representing human subjective perception of sound magnitude

L= k ⋅ log10​(I/​I₀​)

• L - sound loudness, Phon

• k - coefficient depend on frequency, 10

• I - sound intensity, W/m²

• I₀ - threshold of hearing, 10^-12 W/m²

Audibility area

Are between threshold of audibility and threshold of pain/feeling

All sounds we perceive are inside this area

Our ears are sensitive to sound 1000-4000Hz

Human speech is spread over 400-1000Hz

Pitch

Corresponds to sound frequency. Higher the frequency - higher the pitch.

Determined by vibrating c/stics of vocal cords:

Men - 80-100Hz, low pitch

Women - 400-500Hz, high pitch

Timbre

Characterises complex sounds (sound colour)

How is intensity different from loudness?

Intensity is the rate at which a wave's energy flows through a given area. Loudness is a physical response to the intensity of a sound.

Deep-water wave has a wavelength of 10.0 meters. If it travels at 3.0 m/s, what is the wave's period?

Period= wavelength/speed
Period= (10.0 m)/(3.9 m/s)= 2.6 s