Geometry A Vocabulary - Summative 1 (Units 1 and 2)

Flashcards for Geometry A (Units 1 and 2 review)

Undefined terms

Building blocks; point, line, plane

Point

Has no size and no shape

Line

Straight and continues in both directions infinitely

Plane

Flat and extend in two dimensions infinitely with only length and width

Space

The set of all points

Intersection of 2 shapes

All the points that the intersecting figures have in common

Collinear

Points lie on the same line

Non-collinear

Points do not lie on the same line

Coplanar

Points lie on the same plane

Non-coplanar

Points do not lie on the same plane

Postulates

Rules which apply to geometry which are understood; they do not need to be proven to be true

Theorems

Rules that must be proven by applying definitions, postulates, or other theorems

Segment

Part of a line which has 2 endpoints

Ray

Part of a line that has one endpoint and continues in the opposite direction infinitely

Opposite rays

Two rays with a common endpoint that form a line

Angle

2 rays that have a common endpoint

Perpendicular lines

Lines that intersect to form a right angle

Parallel lines

Coplanar lines that don't intersect

Skew lines

Non-coplanar lines that do not intersect

Conditional statement

Has a hypothesis and a conclusion and can be written in the form 'if, then'

Midpoint

Divides a segment into 2 equal parts

Angle bisector

Divides an angle into 2 equal parts

Counter example

Disproves a general statement/conjecture

Biconditional statement

A way to express a true statement & its converse simultaneously

Transversal

Line that intersects 2 or more lines

Corresponding angles

Formed by a transversal and 2 lines where the angles lie on the same side of the transversal either above or below each intersected line

Alternate interior angles

Angles lie between the two lines and on opposite sides of the transversal

Converse

A statement that is formed by switching the hypothesis and conclusion

Inverse

A statement that is formed by negating both the hypothesis and the conclusion

Contrapositive

A statement that is formed by switching and negating both the hypothesis and the conclusion

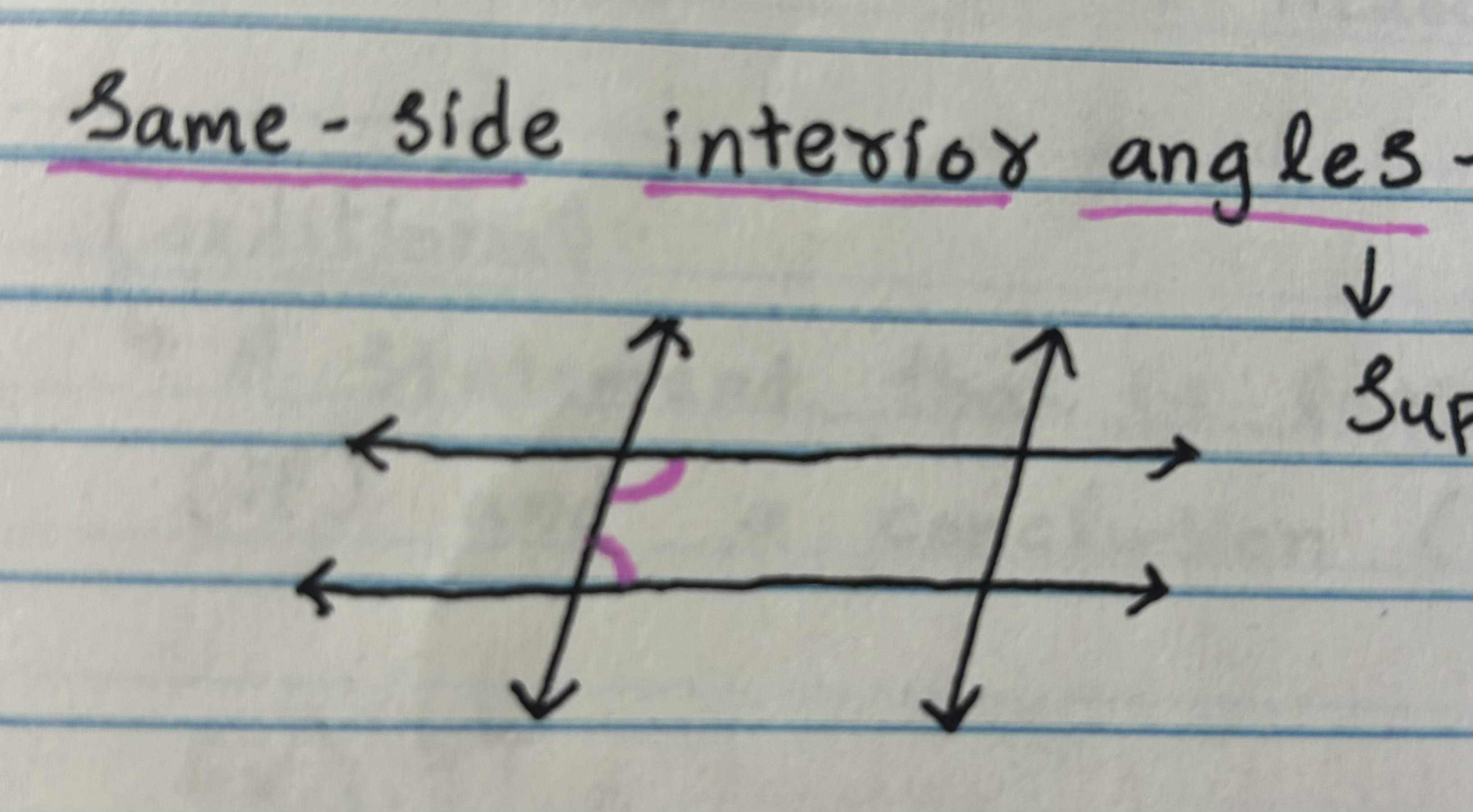
Same-side interior angles

Same position, inside, supplementary = 180 degrees.

Angle theorems

To prove the angles have certain relationships.

Converse theorems

To prove that the lines are parallel

Example question

Facts of spherical geometry

Angle sum for triangles exceed 180 degrees

Parallel lines can intersect in 2 places

Lines do not appear straight, appear curved.

Facts of Euclidean geometry

Angle sum for any triangle is 180 degrees

Parallel lines do not intersect (ever)

Shortest distance between any 2 points is a straight line

How to Identify a plane

Naming 3 non-collider points

key concepts

Set of 3 points is always coplaner.

A set of 4 points or more is only sometimes coplaner.

A set of 3 collinear points may be on more than one plane simultaneously.

A set of 3 non-collinear points exist on only one unique plane.

Any set of 2 points is always collinear.

A set of 3 or more points is only sometimes collinear.

Midpoint formula

Used to determine the midpoint of a line segment, calculated as the average of the x-coordinates and the average of the y-coordinates of the endpoints.

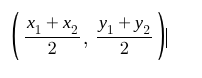
Congruence/Measurement postulate

If 2 line segments have the same measure,then they are congruent.

Segment addition postulate

If A,Z and B are collinear and Z is between points A and B, then: AZ+ZB = AB

Congruence / Measurement postulates(angles)

If two angles have the same measure, they are congruent.

Distance formula for points on a number line

Distance AB, between A and B is given |a-b| or |b-a| = Distance - length!

Distance = length = measure

1.) Subtract points that are given

2.) Find absolute value = (negative number changes to positive number, if a number is positive, then that is the absolute value too- no change required).

3.) Result is the distance between them.