Ultimate AB Calc Cheat Sheet

if k is a positive constant, then the limit as x approaches 0 of (k/x^2) =

positive infinity

if the limit as x approaches a of f(x) = L1 and the limit as x approaches a of g(x) = L2, then the limit as x approaches a of [f(x) + g(x)] =

L1 + L2

if the limits for both f(x) and g(x) DNE but the sums of the right hand and left hand limits are the same, then. . .

the sum is the answer (same for multiplication and division)

the limits of x to the power fractions

remember what ms. pisapia said in class about how the limit as x approaches infinity makes the other numbers insignificant

when you are taking the limit and the denominator is 0, then. . .

the limit will be positive or negative infinity depending on the sign of the function

limit as x approaches 0: sinx/x

1

limit as x approaches 0: (1-cosx)/x

0

derivative of a function definition

f'(x) = limit as h approaches 0 of (f(x+h)-f(x))/h

continuity criteria

1. f(x) exists

2. limit as x approaches a of f(x) exists

3. f(x) = limit as x approaches a of f(x)

jump discontinuity

when the curve "breaks" at a particular place and limits from left and right exist, but they will not match

essential discontinuity

vertical asymptote

removable discontinuity

a "hole" in a graph

even function

graph is symmetrical with respect to the y-axis; f(x) = f(-x)

odd function

graph is symmetrical with respect to the origin; f(-x)=-f(x),

• identical after rotating 180 degrees

if the highest power of x is in the numerator, then

the limit as x approaches infinity is infinity

if the highest power of x is in the denominator, then

the limit as x approaches infinity is zero

if the numerator and denominator have equal powers, then

the limit as x approaches infinity is the coefficients divided by each other

the derivative of a turn in a curve =

0

when does the derivative not exist

1. sharp corners

2. vertical tangent lines/asymptotes

3. cusps

4. discontinuities

d/dx k/x (k is a constant)

-k/(x^2)

d/dx k * sqrt(x)

k/(2sqrt(x))

d/dx sinx

cosx

d/dx cosx

-sinx

d/dx tanx

sec^2x

d/dx cotx

-csc^2x

d/dx secx

secxtanx

d/dx cscx

-cscxcotx

chain rule

f'(g(x))g'(x)

d/dx ln(g(x))

1/g(x) * g'(x)

d/dx e^(g(x))

e^g(x) * g'(x)

d/dx loga(x)

1/xlna

d/dx loga(g(x))

g'(x)/g(x)lna

d/dx a^x (a is a constant)

a^x * ln(a)

d/dx x^x

x^x * (lnx+1)

d/dx a^(g(x)) (a is a constant)

a^x * ln(a) * g'(x)

quotient rule

lowdhigh-highdlow/low^2

product rule

f'(x)g(x)+f(x)g'(x)

d/dx inverse f(x) at y or x = c (constant)

1/f'(inverse of f(c)) (c could be the x or y-coordinate)

d/dx inverse sin(u)

1/sqrt(1-u^2) du/dx

d/dx inverse cos(u)

-1/sqrt(1-u^2) du/dx

d/dx inverse tan(u)

1/(1+u^2) du/dx

d/dx inverse cot(u)

-1/(1+u^2) du/dx

d/dx inverse sec(u)

1/(|u| * sqrt(u^2 - 1)) du/dx

d/dx inverse csc(u)

-1/(|u| * sqrt(u^2-1)) du/dx

when velocity and acceleration have the same signs

particle is speeding up

when velocity and acceleration have opposite signs

particle is slowing down

when the velocity is zero and the acceleration is NOT zero

the particle has momentarily stopped and is CHANGING DIRECTION

volume of a sphere

4/3πr³

surface area of a sphere

4πr²

volume of a conical cone

(1/3)πr²h

slope of tangent line necessary formula

y - y1 = m(x - x1)

normal line

line perpendicular to the tangent line

concave up tangent line

underestimate

concave down tangent line

overestimate

L'Hospital's Rule: 0/0 and infinity/infinity cases

• just take the derivative of both the top and bottom and plug in the c-value

• MUST BE WRITTEN IN FRACTION FORM

• REPEAT UNTIL NOT IN INDETERMINATE FORM (0/0 or infinity/infinity)

limit as x approaches c of f(x)/g(x) = f'(c)/g'(c)

mean value theorem

if f(x) is continuous and differentiable, there's some point in the interval where the slope of the tangent line equals the slope of the secant line that connects the endpoints of the interval

f '(c) = [f(b) - f(a)]/(b - a)

rolle's theorem

if y = f(x) is continuous on the interval [a, b] and is differentiable everywhere on the interval (a, b), and if f(a) = f(b), then there is at least one number c between a and b such that f'(c) = 0

if f'(a) = 0 and f''(a) > 0, then . . .

there is a relative minimum

if f'(a) = 0 and f''(a) < 0, then . . .

there is a relative maximum

how to find vertical asymptotes

set the denominator equal to zero and solve for x

how to find horizontal asymptote

• degree of numerator smaller than degree of denominator - y=0

• degree of numerator same as degree of denominator - y= leading coefficient of numerator/ leading coefficient of denominator

• degree of numerator greater than degree of denominator - no horizontal asymptote

to calculate the absolute extrema. . .

plug in ALL the critical points AND end points and see which y-value is the greatest/least

concavity is when the first derivative is increasing or decreasing, therefore....

if f''(x) > 0, concave up, if f''(x) < 0, concave down

fraction exponent simplify easy formula

look at picture

left riemann sum formula (under the condition that all the rectangles have the same width)

((b-a)/n) [y0 + y1 + y2 + y3 + . . . y(n-1)]

right riemann sum formula (under the condition that all the rectangles have the same width)

((b-a)/n) [y1 + y2 + y3 + y4 + . . . y(n)]

midpoint riemann sum formula (under the condition that all the rectangles have the same width)

((b-a)/n) [y(1/2) + y(3/2) + y(5/2) + y(7/2) + . . . y((2n-1)/2)]

trapezoid rule formula

(1/2)((f(x1)+f(x2))(h) + (f(x2)+f(x3))(h) + . . . )

inscribed vs. circumscribed

all corners of the rectangle lie inside the curve vs. all corners of the rectangle lie outside the curve

riemann sum formula complicated

the image isn't 100% accurate

fundamental theorem of calculus 1

• d/dx ∫ (any constant to x) f(x) dx = f(x) (the constant changing does NOT matter)

• if the upper limit of the integral is a function like x^2, then we multiply the answer by the derivative of that term

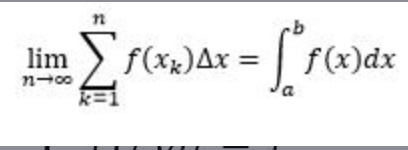
integral of sin(ax) dx

-cos(ax)/a + C

integral of cos(ax) dx

sin(ax)/a + C

integral of sec(ax) * tan (ax) dx

sec(ax)/a + C

integral of sec^2 dc

tan(ax)/x + C

integral of csc(ax) * cot(ax)(dx)

-csc(ax)/a + C

integral of csc^2 (ax)(dx)

(-cot(ax))/a + C

fundamental theorem of calculus 2

∫ f(x) dx on interval a to b = F(b) - F(a)

• used this for that graph question to find f(-6) and f(5) when given the 1st derivative graph

integral of tanx dx

-ln|cosx| + C

integral of cotx dx

ln|sinx| + C

integral of secx dx

ln|secx + tanx| + C

integral of cscx dx

-ln|cscx+cotx| + C

integral of a^x dx

1/ln(a) * a^x + C

integral of 1/sqrt(1-x^2) dx

arcsinx + C

integral of 1/(1+x^2) dx

arctanx + C

Integral of 1/x(sqrt((x^2)-1))

arcsecx + C

when can you use long division to solve for integrals?

when the degree of the numerator is greater than the degree of the denominator

what does the function y = 1/x look like?

look at image

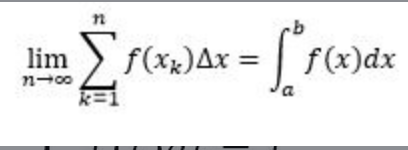
newton's law of cooling

T = (To - Ts) * e^(-kt) + Ts

• Ts = surrounding temperature

• To = initial temperature

ln(1)

0

when the rate of growth is proportional OR exponential...

dy/dt = ky

separation of variables

integration

y = Ce^(kt)

average value of a function on an interval

(1/b-a) (a,b)∫ f(x)dx

how to find the area between 2 curves expressed as a function of x (integral, unit 8)

integral from a to b [f(x) - g(x)]dx

when to integrate with respect to x or y

x: vertical slices, perpendicular to x-axis, when functions are higher than one another ( y = something)

y: horizontal slices, perpendicular to y-axis, horizontally higher (x = something)

equilateral triangle area

(s^2√3)/4

given the hypotenuse of an isoceles right triangle, the area is

((hypotenuse)^2)/4

volume with disc method around the x-axis

pi * integral from a to b [f(x)]^2 dx

volume with disc method around the y-axis

pi * integral from a to b [f(y)]^2 dx

removable discontinuity formula

when you factor the numerator and denominator, the term that you can cancel out is the REMOVABLE DISCONTINUITY