Lecture 2 Linear Alg

vector form of linear system:

can be written more succintly as:

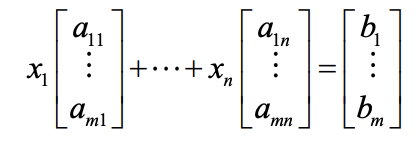
Matrix form of a linear system

Ax=b

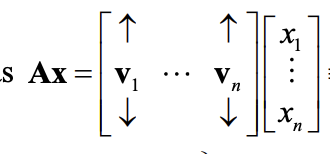
A function T: Rⁿ —> R^m is a linear transformation if T satisfies the linearity property T(x) = T(c1v1 + c2v2) = _____

• Or if there exists an nxm matrix A such that T(x) = ___

• any function of the form L(x) =ax + b is not linear unless b = __

A(x)

0

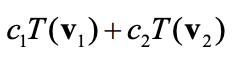
standard or elementary basis vectors e1, e2, … en

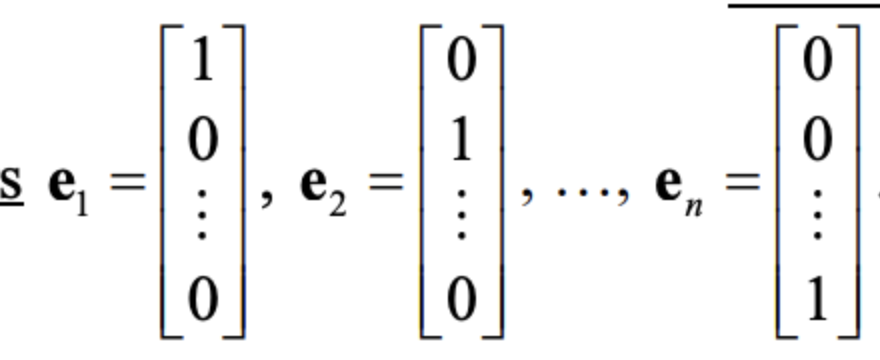
Ae_n =

v_n

nth column of matrix A

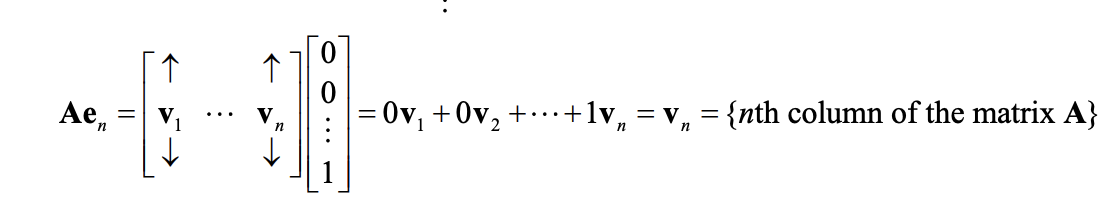
Identity function Id Rⁿ → Rⁿ is simply Id(x)=x

Identity matrix I_n

This matrix has 0’s everywhere except on the main diagonal, and all of the diagonal entries are equal to 1.

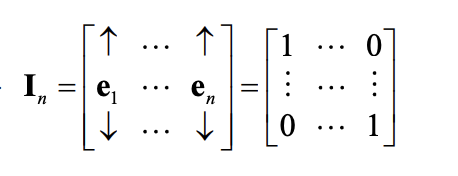
Dilation (scaling) is a transformation of the form T (x) = rx for r>0

Matrix A:

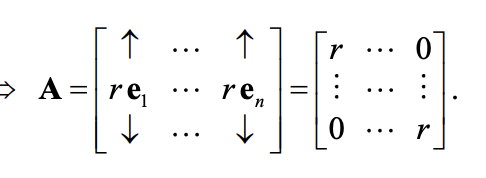
Counterclockwise rotation in R2 Matrix Rθ

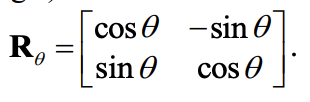
Rotation-dilation in R2 Matrix A:

If we let a =rcosθ and b =r sinθ we see any matrix of form _____

will represent a rotation-dilation where the scaling is by r= ____ and the angle of rotation is determined by θ =___

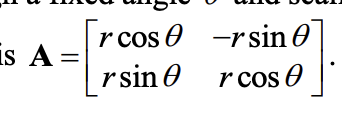
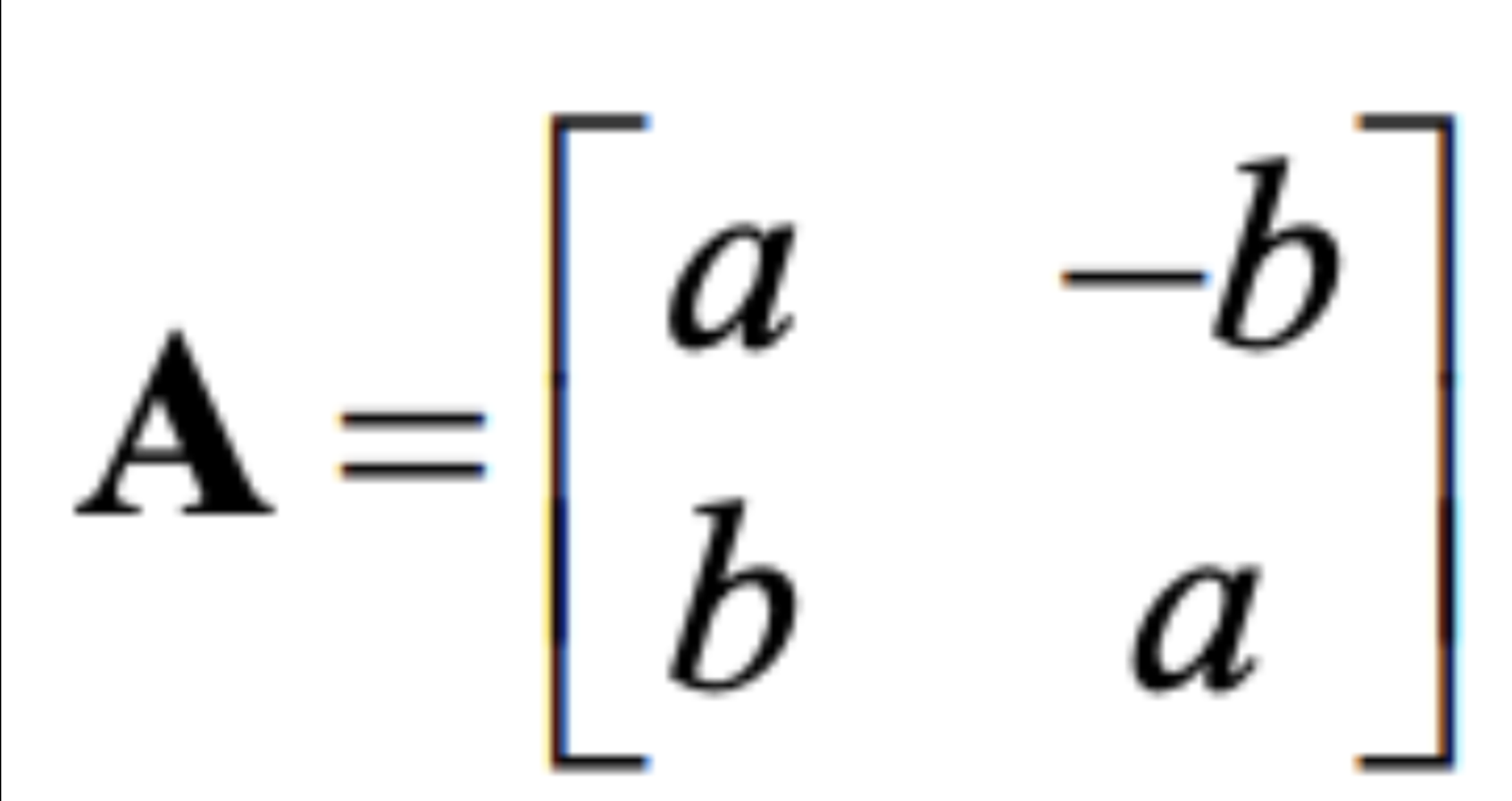
√(a²+b²), tan^-1(b/a) in appropriate quadrant

Orthogonal projection of x onto L if u is a unit vector parallel to L:

T(x) = projL(x) is linear, how to create matrix:

do T(e1), T(e2) for each en

Reflection of vector x through a line L:

Matrix of reflection:

2projL(x) - x

2A-I

A respresents matrix of orthogonal proj

Horizontal Shear w/ dilation matrix A3

Vertical Shear w/ dilation matrix A4

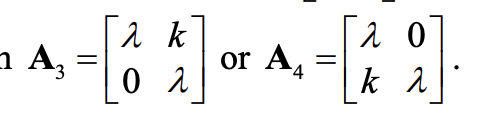
Solving for inverse matrix A^-1, going from y -> x

• Represent the two equations as a matrix:

• Do row reduction rref [ A | I_n| to see if u can get:

  • If left half fails to be I_n, then A is not invertible

• If the matrix A has full rank __, then we will be able to solve uniquely for x in terms of y

[A | I_n]

[I_n | A^-1]

n

if det(A) is not 0, or else A will not have full rank and will not be invertible

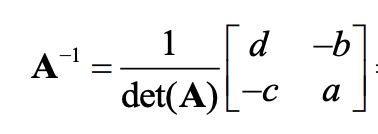
refLx matrix is of form

where a²+b²=1

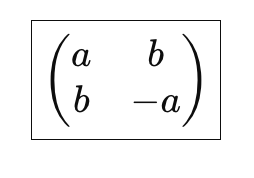
how to do dot product of two vectors

multiply the values of the same row, then add up all the sums of the rows

how to multiply matrixes: ___

If A is mxn and B is nxp (n must be same for both, meaning ___ of A must equal ___ of B), AB is ___

Row of the first × column of the second

columns, rows

mxp

a linear transformation from Rn to Rm is represented by an __ x _ matrix

Build the matrix by doing T(___) for how ever many ___ you need

mxn matrix

e1, e2, etc. columns/previous n dimensions