Princeton Review AP Calculus BC, Chapter 12: Infinite Sequences and Series

Sequences & Series

Sequence: An infinite succession of numbers that follow a pattern * Usually denoted with a subscript using aₙ * Usually the terms are generated by a formula, ex. aₙ=(n-1)/n beginning with n=1 is 0, 1/2, 2/3, etc. * n is always an integer
Officially: * “A sequence has a limit L if for any ε>0 there is an associated positive integer N such that |aₙ - L| < ε for all n ≥ N. If so, the sequence converges to L and we write lim (n → ∞) aₙ = L” * If a sequence has no finite limit, it diverges.

Infinite Series
An infinite series is an expression of the form a₁ + a₂ + a₃… + aₖ + …. The numbers a₁, a₂, a₃, etc. are the terms of the series * In other words, an infinite series is a sequence of terms where the terms are added up, there is a pattern to the order of the terms, and there are an infinite number of terms.

As n increases, the partial sum includes more and more terms of the series. So if aₙ approaches a limit as n approaches ∞, then this limit is likely to be the sum of all of the terms in the series, thus a convergence. * If the sequence of partial sums converges to a limit S, then the series is said to converge and S is called the sum of the series. * If the sequence of partial sums diverges (doesn’t have a limit), then the series is said to diverge which means that a divergent series has no sum.

Geometric Series

Used in the form of ∞Σ(n=1) a*r^(n-1)

\ * These show up often on the AP exam: often asked to determine whether the series converges or diverges, and if it converges, to what limit. * If |r|

For example, the series (1/2)+(1/2^2)+(1/2^3) converges, while 2+2^2+2^3 diverges.

If a geometric series converges, you can figure its sum out by doing the following: * Multiply the expression by r * aₙ = a + ar + ar^2 + ar^3… + ar^(n-1) → raₙ = a + ar + ar^2 + ar^3… + ar^(n-1) * Subtract the second expression from the first * aₙ - raₙ = a - ar^n * Factor out aₙ from the left side * aₙ(1-r)=a-ar^n * Divide through by (1-r) * aₙ=(a(1-r^n))/(1-r)

If we want to find the sum of the first n terms of a geometric series, we use the following formula:

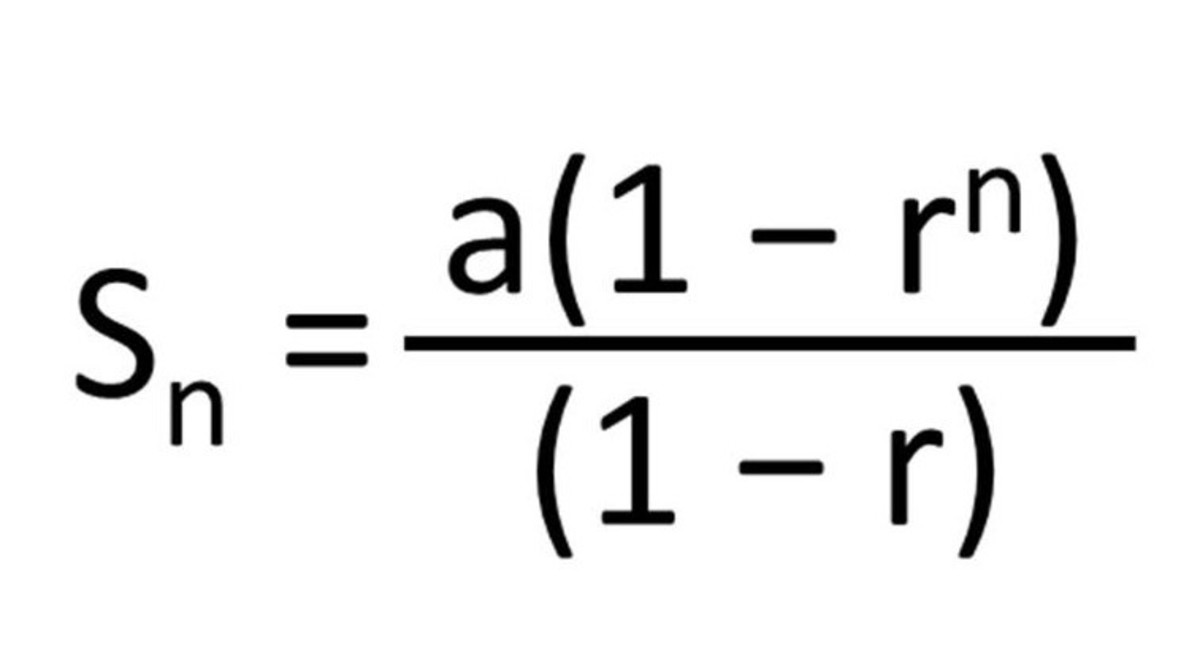
For an infinite geometric series, if it converges, lim (n→∞) r^n = 0, and its sum is found this way: * S = (a)/(1-r)

The nth Term Test For Divergence
The nth term test means we find the limit of the series and see if we get zero or not * If the limit = L (any number other than 0), the series diverges * If the limit = 0, we need to choose a different test

Integral Test for Convergence * If f is positive, continuous, and decreasing for x≥1, and aₙ=f(n), then

Either both converge or both diverge.

In other words, if you want to test convergence for a series with positive terms, evaluate the integral and see if it converges.

Harmonic Series & P-series

Harmonic Series: (1/n) pattern

Might look as though it is converging, but it diverges
The sums are not approaching a limit, so as the sequence of partial sus diverges, so does the sequence of partial sums for the harmonic series

\ p-Series

A series of the form (1/n^p) converges if p>1 and diverges if 0<p<1

Tests for Convergence

Comparison Tests for Convergence

Let 0 ≤ aₙ ≤ bₙ for all n * If the summation of bₙ from 1 to ∞ converges, then the summation of aₙ from 1 to ∞ converges * If the summation of aₙ from 1 to ∞ diverges, then the summation of bₙ from 1 to ∞ diverges
Essentially, if all of the terms of a series are less than those of a convergent series, then it too converges. If all of the terms of a series are greater than those of a divergent series, then it too diverges

\ Limit Comparison Test

Alternating Series Test for Convergence

Used for terms that alternate between positive and negative
The series using (-1)^(n+1) bₙ converges if the following conditions are all satisfied * bₙ > 0 (which means that the terms must alternate in sign) * bₙ > bₙ₊₁ for all n * bₙ → 0 as n → ∞

Absolute Convergence Theorem:

The series Σaₙ converges absolutely if the corresponding series Σ|aₙ| converges

Ratio Test for Convergence

Determining Absolute or Conditional Convergence

Sometimes, an alternating series will converge, but when we look at the absolute value of the terms, it doesn’t.
An alternating series that is not absolutely convergent is called conditionally convergent

\ Alternating Series Error Bound

When summing an alternating series with a finite number of terms, the sum will not be the same as the sum with an infinite number
If we want to find the error, we need to evaluate | S-Sₙ |
Can put a bound on the error: a number that the error is less than, which is simply the absolute value of the next term in the alternating series * If summing the first 10 terms in an alternating series, the error will be less than the absolute value of the eleventh term

\ Finding Taylor Polynomial Approximations of Functions

We can approximate a function on an interval centered at x=a by using a Taylor series (if centered about x=0, it’s a Maclurin series).
In a Taylor polynomial, the terms are found from thee derivatives of f as follows: * If f can be differentiated n times at a, then the nth Taylor polynomial about x=a is * pₙx = f(a) + f’(a)(x-a) + (f’’(a)/2!)(x-a)^2+ (f’’’(a)/3!)(x-a)^3+… + (f^(n)(a)/n!)(x-a)^n(x-a)^n

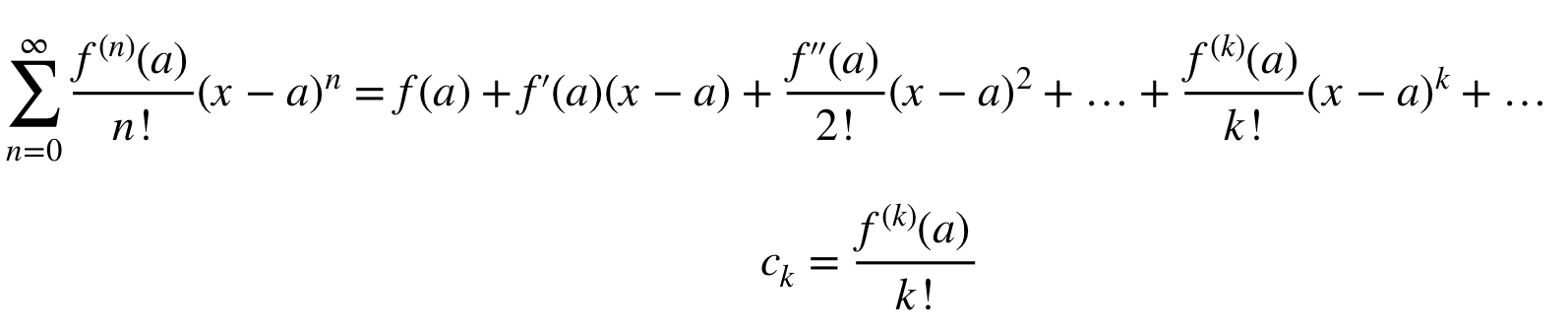
Lagrange Error Bound

The “error bound” of a Taylor polynomial, aka the Lagrange error

If you are finding an nth degree Taylor polynomial, a good approximation to the error bound is the next nonzero term in a decreasing series.

\ Radius and Interval of Convergence of Power Series

Going from n = 0 to n = ∞ instead of n = 1 to n = ∞
Radius of convergence: R. * If the series converges only for x=0, the radius of convergence is 0 * If the series converges absolutely for all x, the radius is all x * Set of all values of X (-R, R) is the interval of convergence

\ Representing Functions as Power Series

We can use differentiation and integration of power series to find the power series of other functions
Can approximate the integral using its Maclurin and approximate the solution using the aforementioned series
Find a new Taylor series from a known Taylor series.