electrons in atoms unit 3

describe light

light is an electromagnetic wave which carries energy. different colors of light correspond to different wavelengths and frequences

describe the order for wavelength

decreasing to increasing

• gamma rays

• x-rays

• rainbow (violet to red)

• infrared

• microwave

• radio

describe the order for energy

decreasing to increasing

• radio

• microwave

• infrared

• rainbow (red to violet)

• x-rays

• gamma rays

describe the order for frequency

decreasing to increasing

• radio

• microwave

• infrared

• rainbow (red to violet)

• x-rays

• gamma rays

describe frequency

Frequency, ν, is the number of peaks passing the observation point per unit time.  The SI unit of frequency is Hz, (1 Hz = 1 s‒1 ).

describe wavelength

Wavelength, λ, is the distance between peaks measured in m.  Nanometers (1 nm = 10‒9 m) are often used in the case of visible light.

whats the equation for speed of waves

c (speed of light)= wavelenght * frequency

describe the connection between frquency wavelgnth and energy of light

• Frequency and wavelength of light are inversely proportional

• The energy of light is proportional to frequency. 𝐸 = ℎv

describe diffraction

the bending of waves around corners. Constructive and destructive interference patterns.

describe refraction

the bending of light as its speed changes in passing from one medium to another

what is blackbody radiation

all objects emit electromagnetic radiation due to thermal energy (except at 0 K)

what is the ultraviolet catastrohpe

Classical wave theory could not predict observed spectra

describe what max planck did

• Planck explained the observed spectrum – its exact shape – by postulating that light energy is quantized.

• The smallest increment of light energy is the energy of a single particle of light, a photon.

• The energy of one photon of light with frequency, ν, is given by 𝐸𝑝ℎ𝑜𝑡𝑜𝑛 = ℎ𝜈 where h = 6.62606957×10‒34 Js is called Planck’s constant

what does the voltmeter do

Voltmeter → measures how fast the e- are going (Kinetic Energy)

what does the ammeter

how many e- are ejected and travelling (Current)

describe the photoelectric efffect

Sufficiently high frequency/energetic photons eject electrons from the surface of a metal.

• Ephoton > Ethreshold

• Ethreshold = work function of the metal, symbol Φ

• Φ changes with different metals

what section has the smallest work function

Alkali metals have the smallest work functions - it takes less energy to eject an electron from an alkali metal.

• According to decreasing work function,  lithium > sodium > potassium > rubidium > cesium.

describe the work function

If Ephoton > Φ, then the excess energy goes towards the kinetic energy of the ejected electron

Exactly one electron is ejected from the metal surface for every one photon of light (provided it is energetic enough).

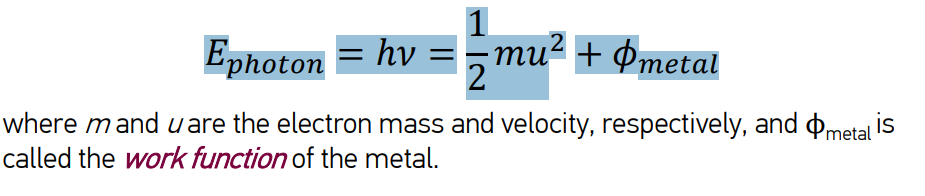
describe daltons atom

single, indivisible entity unique for each element, cannot be altered or destroyed and combines to more complex compounds

describe plum pudding model

negative charged “corpuscles” (electrons) embedded in a sea of positive charge

describe nucluer model

highly concentrated positive charge in a very small volume which contained the bulk of the atom’s mass surrounded by orbiting electrons

describe energy of electron transition

The difference between two of these energies determines a transition energy equal to the energy of the photon emitted or absorbed.

• E > 0: absorption of a photon

• E < 0: emission of a photon

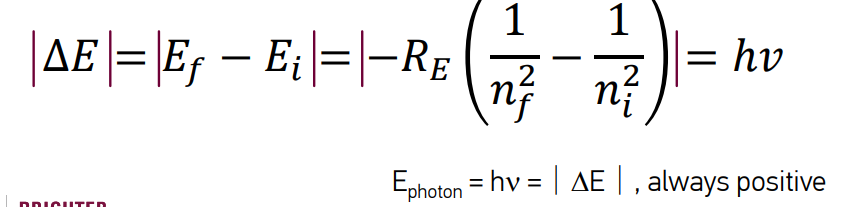
describe what de broglie did

• Electrons & nuclei, & light are all treated as wave-like & particle-like

• de Broglie first suggested that particles, such as electrons, are wavelike, characterized by a wavelength

• The wavelength of matter (in meters) is equal to the ratio of Planck’s constant over the product of the mass (in kg) times the velocity (in m/s).

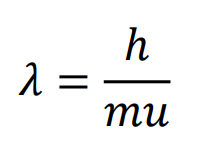
what is the Heisenberg Uncertainty Principle

There is uncertainty in the position of an electron in an atom.

• One can only speak of the probability of finding the electron in a volume within the atom.

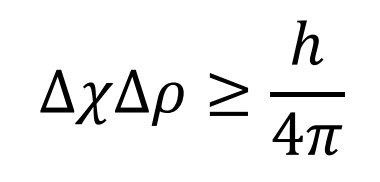
describe the wave function

• The solutions to Schrodinger’s Equation correspond to a wave function, Ψ, which (together with the spin) describes the state of the electron in the atom as a wave

• The square of the wave function, Ψ2 , at each position gives the likelihood of finding the electron in that location.

• The region of space where we find an electron 90% of the time defines the boundaries of the orbital

describe the pinicpal qunatum number (n)

• The Principal Quantum Number describes the energy and distance of the electron from the nucleus

• It is analogous to the energy levels in the Bohr Model of the Atom

• The greater the value of n, the further the electron is from the nucleus and the more energy it has

• n=1,2,3,…

describe angular momentum number (ℓ)

• Because of the spherical symmetry of the hydrogen atom (and electron spin), there is more than one state for each energy level.

• The electron in hydrogen has an orbital angular momentum associated as it orbits about the proton nucleus.

• Angular momentum (azimuthal) has a magnitude, with associated quantum number - angular momentum quantum number

• ℓ = 0, 1, 2, …, n ‒1

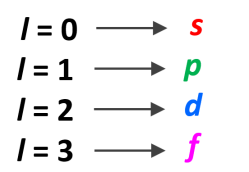
describe magnetic quantum number (mℓ)

• Angular momentum has an orientation-associated quantum number - magnetic quantum number

• Orbitals with the same angular momentum number are degenerate in energy

• mℓ = ‒ℓ, ‒ℓ + 1, …, ℓ ‒1, ℓ

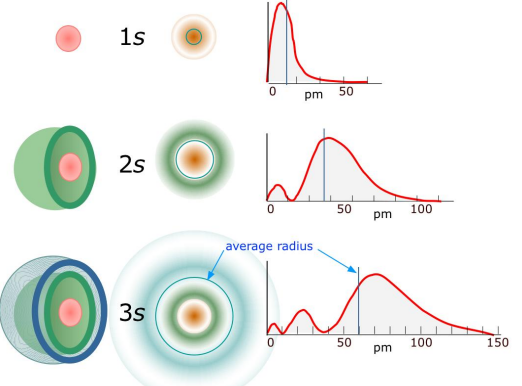
describe s orbitals

• The ℓ = 0 orbitals have spherical shape. m ℓ = 0

• Between nodes is a radial node

• The ns orbital has n – 1 radial nodes.

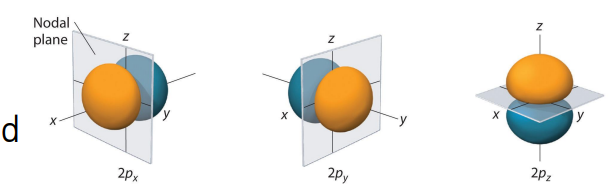
describe p orbitals

• The ℓ = 1 orbitals have dumbell shape.

• Three degenerate np orbitals mℓ = -1, 0, +1

• Angular nodes between positive and negative lobes

• The np orbital has n – 2 angular nodes.

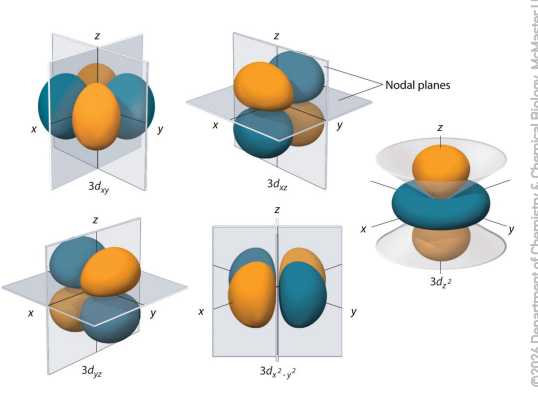
describe d orbitals

• The ℓ = 2 orbitals have clover shape.

• Five degenerate np orbitals mℓ = -2, -1, 0, +1, +2

• Angular nodes between positive and negative lobes

describe the spin quantum number

• In addition to the orbital quantum numbers already introduced, the electron has a spin quantum number,

• ms = ½ or ‒½, spin angular momentum pointing up or down, respectively.

• There are two states associated with the lowest energy level: (n, ℓ, mℓ , ms ) = (1, 0, 0, ½) and (1, 0, 0, ‒½)

describe one electron systems

Ions with only one electron – i.e., He+ , Li2+,…, have the same orbitals as hydrogen, except that they held more closely to the nucleus by the larger nuclear charge.

• ex. The energy levels of He+ are four times deeper than those of H because the nuclear charge is doubled.

describe multielectron systems

• Electron repulsion makes calculating the states and energy levels difficult – computers approximate this

• Each electron is assigned to an orbital

describe Pauli Exclusion Principle

two electrons with the same spin cannot occupy the same orbital.

describe Ground State Electron Configuration

set of occupied orbitals filled in order of increasing energy

• Aufbau’s Principle – the occupation of electrons in order of increasing orbital energy

descirbe nucleur shielding

• For one electron species, the greater the nuclear charge (Z), the lower the energy of the electron.

• For multielectron species, electrons repulsions destabilize the electrons (shielding – S) and increase their potential energy

describe the effective numcleur charge equation

Inner electrons shield outer electrons from the full attractive charge from the nucleus (effective nuclear charge) Zeff = Z – S

• Orbitals that penetrate closer to the nucleus experience a higher effective nuclear charge and reduced shielding (s > p > d > f)

what is hunds rule

electrons occupy degenerate orbitals singly first to avoid repulsions (pairing energy)

describe the Electron Configuration Exceptions

describe paramagnetic

atoms with unpaired electrons that are attracted to magnetic fields

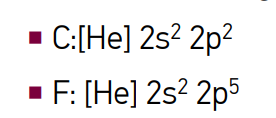
describe diamagnetic

atoms with entirely paired electrons that are weakly repelled by magnetic fields

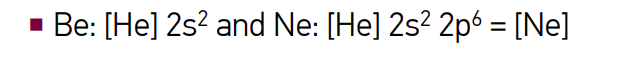
describe the devlopement of the periodic table

• Dmitri Mendeleev (1834 – 1907 CE) formulated the Periodic Law and the Periodic Table of Elements which predicted elements yet discovered

• Mendeleev organized the known elements into eight groups, in order of increasing mass. He left gaps for undiscovered elements and predicted their properties