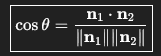Vectors Formulae (Shortest Distance, Angle Between)

Point Line

• Take the vector from a point on the line to your point.

• Cross it with the line’s direction vector.

• Divide the length of that cross product by the length of the line’s direction vector.

• ✅ Gives the shortest (perpendicular) distance.

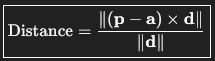
Skew Lines

• Take the vector connecting any point on line 1 to any point on line 2.

• Dot it with the cross product of the two lines’ direction vectors.

• Take the absolute value and divide by the length of the cross product of the directions.

• ✅ Gives the shortest distance between the lines.

Angle Line and plane

• Take the line’s direction vector.

• Dot it with the plane’s normal vector.

• Divide by the product of their lengths.

• Take the arcsine of that value.

• ✅ This gives the angle between the line and the plane.

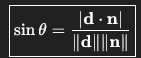
Angle Plane and plane

• Take the normals of the two planes.

• Dot them together and divide by the product of their lengths.

• Take the arccosine of that value.

• ✅ This gives the angle between the planes.