S2.1 Ionic Bonding - Retake

Guiding question — What determines the ionic nature and properties of a compound?

• Ionic character increases with greater ΔEN (metal + non‑metal, large electronegativity difference) and with small, highly charged cations plus large, highly polarizable anions (Coulomb’s law + polarization argument). Your notes frame this as “electrostatic attraction between oppositely charged ions in a lattice.”

• Structure: a giant ionic lattice (not molecules) → high mp/bp, brittleness, low volatility, conducts only when ions are mobile (molten/aqueous), and often soluble in polar solvents via ion–dipole interactions.

• Strength of ionic bonding measured by lattice enthalpy (ΔH°_latt): increases with higher ionic charges and smaller ionic radii → stronger electrostatic attractions → higher mp and lower volatility.

• Non‑metals (high EN) gain e⁻ to attain noble‑gas configurations, forming anions (e.g., O + 2e⁻ → O²⁻; Cl + e⁻ → Cl⁻). Your notes treat this in “6.1 Ionic bonding” with the electron transfer picture.

• IB positions this in Structure 1: ionic bonding and expects symbol/equation fluency.

Predict the charge of an ion from the electron configuration (include transition elements).

• s‑/p‑block rule of thumb:

  • Group 1 → +1, Group 2 → +2, Group 13 → +3; Group 15 → −3, Group 16 → −2, Group 17 → −1 (to reach ns² np⁶).

• Electron configuration approach: remove outermost (highest n) s‑electrons first; for anions, fill to octet (e.g., Na [Ne]3s¹ → Na⁺; O [He]2s²2p⁴ → O²⁻). Your notes provide the electron‑transfer narrative.

• Transition elements: variable charges because successive ionization energies of ns and (n−1)d electrons are comparably spaced; removal can continue to different totals → variable oxidation states (Fe²⁺/Fe³⁺, Cu⁺/Cu²⁺).

Structure 3.1 — How does periodic position relate to ion charge(s)?

From periodic trends:

• Metals (left) form cations with charges matching group number (1 → +1, 2 → +2, 13 → +3).

• Non‑metals (right) form anions to complete octet (17 → −1, 16 → −2, 15 → −3).

• Transition metals show multiple possible charges; use Stock notation in names.

AHL Structure 1.3 — Why do successive ionization‑energy trends in transition elements explain variable oxidation states?

In transition metals, the ns and (n−1)d subshells are close in energy → successive ionization energies do not jump sharply after removing ns electrons; it remains feasible to remove additional electrons from (n−1)d → multiple stable cationic states (e.g., Ti²⁺, Ti³⁺, Ti⁴⁺).

Deduce the formula and name of an ionic compound from its component ions (incl. polyatomic ions).

• Balance total charge to zero to get empirical formula (e.g., Al³⁺ + SO₄²⁻ → Al₂(SO₄)₃).

• Naming rules: cation first, then anion; for binary salts the anion takes “-ide” (sodium chloride, magnesium oxide). For transition metal cations, use Stock numerals (iron(III) chloride). IB emphasizes interconversion name↔formula; your notes include worked ionic examples.

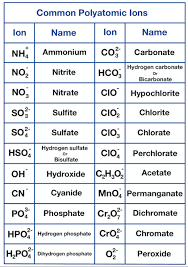
Polyatomic Ions

Ammonium NH₄⁺, hydroxide OH⁻, nitrate NO₃⁻, hydrogencarbonate HCO₃⁻, carbonate CO₃²⁻, sulfate SO₄²⁻, phosphate PO₄³⁻.

Reactivity 3.2 — Why is forming an ionic compound from elements a redox reaction?

• Metal atoms are oxidized (lose e⁻): Na → Na⁺ + e⁻.

• Non‑metal atoms are reduced (gain e⁻): ½Cl₂ + e⁻ → Cl⁻.

• Combine → overall redox forming the ionic lattice (Na(s) + ½Cl₂(g) → NaCl(s)). Covered in your notes’ ionic bonding section and IB reactivity links.

AHL Structure 2.2 — How is formal charge used to predict the preferred structure of sulfate?

• Formal charge on an atom = valence − [nonbonding + ½(bonding)]. Structures with lower magnitudes of FC and negative charge on the more electronegative atoms (O) are preferred.

• Sulfate, SO₄²⁻: best described by resonance with overall FCs distributed primarily on O; choose drawings that keep S close to 0 and O at −1/0 patterns rather than placing positive charge on O. IB asks you to use FC to rationalize the preferred depiction.

AHL Reactivity 3.1 — Polyatomic anions are conjugate bases of common acids.

Examples: NO₃⁻ from HNO₃, SO₄²⁻ from H₂SO₄, CO₃²⁻ from H₂CO₃, HCO₃⁻ from H₂CO₃ (one deprotonation), PO₄³⁻ from H₃PO₄, OH⁻ from H₂O. IB emphasizes acid–base conjugate pairs.

Relationship between stability of the anion and the conjugate acid’s Ka

• Stronger acid → larger Ka → weaker conjugate base (i.e., the anion is more stable/less reactive).

• Conversely, weaker acid (small Ka) → conjugate base is stronger/less stabilized. IB’s AHL reactivity outcomes expect this link.

Explain the physical properties of ionic compounds: volatility, electrical conductivity, solubility.

• Volatility: very low because giant ionic lattices need large energy to separate ions (strong electrostatic attractions).

• Electrical conductivity: do not conduct as solids (ions fixed), but do conduct when molten or aqueous (mobile ions carry charge).

• Solubility: often soluble in polar solvents (e.g., water) due to ion–dipole attractions that compensate for lattice enthalpy; solubility varies with ΔH°_soln (lattice vs hydration enthalpies).

Include lattice enthalpy as a measure of ionic bond strength; influence of radius and charge.

• Definition (IB): ΔH°_latt is the enthalpy change when one mole of an ionic solid is separated into gaseous ions (endothermic, positive by dissociation definition). Your notes treat lattice enthalpy explicitly.

• Trends:

  • Higher ionic charges → larger ΔH°_latt.

  • Smaller ionic radii (shorter r) → larger ΔH°_latt.

Tool 1, Inquiry 2 — What experimental data demonstrate ionic physical properties?

• Melting/boiling point data (e.g., NaCl high mp) demonstrate strong ionic bonding.

• Conductivity tests: solid NaCl (no current), molten NaCl / NaCl(aq) (lamp lights) → need mobile ions.

• Solubility tests: ionic solids dissolving in water but not in non‑polar solvents → ion–dipole vs dispersion.

• Your notes highlight these property‑evidence links under “Ionic bonding” learning outcomes.

• IB Topic overview also emphasizes linking experimental evidence to structure/properties.

Structure 3.1 — Use lattice enthalpies & the bonding continuum to explain melting points of metal chlorides across Period 3.

• NaCl (Na⁺ Cl⁻): classic ionic lattice → high mp.

• MgCl₂ (Mg²⁺ Cl⁻): higher cation charge strengthens lattice, but structure and coordination keep mp also high.

• AlCl₃ (Al³⁺ Cl⁻): very high charge density Al³⁺ strongly polarizes Cl⁻, inducing covalent character; AlCl₃ tends to form molecular/dimeric species (esp. in vapor/anhydrous forms), giving a much lower mp compared with NaCl/MgCl₂ — a drop that reveals the ionic→covalent continuum rather than a monotonic increase with charge. Your notes point to using lattice enthalpy and polarization to rationalize such trends.

Define Ionic Bonding

“The ionic bond is formed by electrostatic attractions between oppositely charged ions.”

Explain

Why ionic crystals are brittle:

• Ions sit in a 3D, alternating +/− lattice held by strong electrostatic attractions.

• When a shear force shifts one layer relative to another, like charges are forced adjacent (e.g., Cl⁻ over Cl⁻, or Na⁺ over Na⁺).

• Strong repulsion between like charges causes the layers to separate along planes → the crystal shatters (brittle). Your notes explicitly flag brittleness as a key property of ionic lattices.

Deduce (formulas & names with polyatomic ions)

Naming rule (IB): Cation first, then anion; binary anions end with “-ide.” Know the required polyatomic ions by name & formula: NH₄⁺, OH⁻, NO₃⁻, HCO₃⁻, CO₃²⁻, SO₄²⁻, PO₄³⁻.

Examples:

• Ca²⁺ with HCO₃⁻ (charge −1): need 2 anions to balance +2 → Ca(HCO₃)₂. Name: calcium hydrogencarbonate. (Method: cross‑balance charges to get total 0.)

• NH₄⁺ with SO₄²⁻: need 2 ammonium ions to balance −2 → (NH₄)₂SO₄. Name: ammonium sulfate. (Your notes list all required polyatomic ions.)

Discuss (qualitative solubility: hydration vs lattice enthalpy)

• To dissolve, water must pull ions from the lattice and solvate them with ion–dipole attractions.

• Competing energies:

  • Lattice enthalpy (formation): how much energy you “lose” when breaking the solid (must overcome this). Larger |ΔH°_latt| → harder to dissolve.

  • Hydration enthalpy (of the gaseous ions): energy released when ions are surrounded by water. More negative hydration enthalpies (small/high‑charge ions) → easier to dissolve.

• Qualitative rule: A salt is more likely soluble when the sum of hydration enthalpies (favorable) offsets the lattice enthalpy (unfavorable). Your notes directly link ion charge and radius to larger lattice enthalpies and note ion–dipole interactions underlying solubility.

1. What is ionic bonding?

• Ionic bonding is the electrostatic attraction between oppositely charged ions (cations and anions).

• It usually occurs between metals (which lose electrons to form cations) and non-metals (which gain electrons to form anions).

• The resulting compound is electrically neutral — total positive charge equals total negative charge.

• It’s a strong, non-directional force, acting in all directions throughout the lattice.

• Example: Sodium chloride (NaCl) → Na⁺ and Cl⁻ held together by ionic bonds.

2. How do metals and non-metals form ions?

• Metals:

  • Lose electrons from their outer (valence) shell to achieve a noble gas configuration.

  • Form positive ions (cations) because losing electrons leaves more protons than electrons.

  • Example: Na → Na⁺ + e⁻

• Non-metals:

  • Gain electrons to fill their outer shell and achieve a noble gas configuration.

  • Form negative ions (anions) because gaining electrons makes electrons outnumber protons.

  • Example: Cl + e⁻ → Cl⁻

3. Why is ion formation energetically favourable?

• Atoms tend toward stable electron configurations like noble gases.

• For metals, losing a few outer electrons is easier (requires less energy) than gaining many.

• For non-metals, gaining a small number of electrons is easier than losing many.

• Energy changes involved:

  • Ionization energy (endothermic) — energy required to remove electrons from the metal.

  • Electron affinity (exothermic) — energy released when the non-metal gains electrons.

• The overall process releases energy when the lattice forms (lattice enthalpy), making it favourable.

4. How can you predict the charge on an ion?

• From group number in the periodic table:

  • Group 1 → +1

  • Group 2 → +2

  • Group 13 → +3

  • Group 15 → –3

  • Group 16 → –2

  • Group 17 → –1

• Transition metals:

  • Can form ions with variable charges due to similar energies of outer s and d electrons.

  • Roman numerals in names indicate the charge: e.g., Copper(II) oxide → Cu²⁺O²⁻, Copper(I) nitrate → Cu⁺(NO₃⁻)

  • This is called Stock notation.

5. What is a binary ionic compound?

• A compound made from only two different elements: one metal cation, one non-metal anion.

• The cation is named first, then the anion (ending in -ide).

• Example: Na + I → sodium iodide.

6. What are polyatomic ions and why are they important?

• Polyatomic ions: ions made of two or more atoms bonded covalently, carrying an overall charge.

• Common examples to memorise:

  • Ammonium: NH₄⁺

  • Hydroxide: OH⁻

  • Nitrate: NO₃⁻

  • Hydrogencarbonate: HCO₃⁻

  • Carbonate: CO₃²⁻

  • Sulfate: SO₄²⁻

  • Phosphate: PO₄³⁻

• Naming compounds with polyatomic ions: name the cation first, then the polyatomic ion (no -ide change if the anion is polyatomic).

7. What is the structure of ionic compounds?

• Ionic compounds form giant 3D crystal lattices.

• Positive and negative ions arranged in a regular, repeating pattern for maximum attraction and minimal repulsion.

• Ratio of ions corresponds to empirical formula (e.g., NaCl has a 1:1 ratio).

• Each ion is surrounded by oppositely charged ions in all directions.

• The structure is held together by strong electrostatic attractions.

What are the physical properties of ionic compounds and why do they occur?

• High melting & boiling points:

  • Strong electrostatic forces require a lot of energy to break.

  • Higher ion charge density → stronger attractions → higher melting points (e.g., MgO > NaCl).

• Brittleness:

  • Stress causes like-charged ions to align → strong repulsion → lattice shatters.

• Solubility in water:

  • Water is polar; partial charges attract ions, forming ion–dipole interactions that pull the lattice apart.

• Electrical conductivity:

  • Solid: non-conductive (ions fixed in place).

  • Molten or dissolved: conductive (ions free to move).

9. What is lattice enthalpy and what factors affect it?

• Lattice dissociation enthalpy (ΔHₗₐₜₜᵒ):

  • Energy required to separate 1 mole of an ionic solid into gaseous ions.

  • Always positive (endothermic).

  • Larger ΔHₗₐₜₜᵒ → stronger ionic bonds.

• Factors increasing lattice enthalpy:

  • Higher ionic charges → stronger attraction.

  • Smaller ionic radii → ions closer together → stronger attraction.

• Examples:

  • MgO has higher ΔHₗₐₜₜᵒ than NaCl because Mg²⁺ and O²⁻ have higher charges and smaller sizes.

10. Why is the formation of an ionic compound a redox reaction?

• Metal is oxidised: loses electrons → oxidation.

• Non-metal is reduced: gains electrons → reduction.

• Oxidation and reduction happen simultaneously → redox reaction.

11. How do you determine the formula of an ionic compound?

• Find charges of cation and anion.

• Combine them in the smallest ratio so total charge = 0.

• Examples:

  • Al³⁺ and O²⁻ → Al₂O₃.

  • Ca²⁺ and NO₃⁻ → Ca(NO₃)₂.

12. How do you relate ionic bonding to periodic trends?

• Metals on the left of the periodic table:

  • Low ionization energies → lose electrons easily.

• Non-metals on the right:

  • High electron affinities → gain electrons easily.

• Down a group:

  • Larger ionic radius → lower lattice enthalpy → lower melting point.

• Across a period:

  • Greater nuclear charge & smaller size → higher lattice enthalpy.

13. What is meant by the “bonding continuum” and covalent character in ionic bonds?

• Bonding is not purely ionic or purely covalent; it exists on a continuum.

• Covalent character in ionic bonds arises when:

  • The cation is small and highly charged → high polarizing power.

  • The anion is large and easily distorted → high polarizability.

• Distortion of the electron cloud in the anion causes sharing of electron density → covalent character.

• Example: AlCl₃ shows significant covalent character compared to NaCl.

• Trend: Higher charge density → greater covalent character → lower-than-expected melting point.

14. How can formal charge help predict the preferred structure of sulfate?

• Formal charge: hypothetical charge if electrons were shared equally.

• Formula:
  FC = (valence electrons in free atom) – (nonbonding electrons) – (bonding electrons ÷ 2)

• In sulfate (SO₄²⁻):

  • Different resonance structures can be drawn.

  • The preferred structure minimizes formal charges and places negative charges on the more electronegative atoms (oxygen).

• In IB HL, this is used to justify why double bonds in sulfate are often shown as delocalised rather than fixed.

18. How does lattice enthalpy explain solubility trends?

• Dissolving an ionic solid requires:

  • Breaking the ionic lattice (endothermic, lattice enthalpy).

  • Hydrating the ions (exothermic, hydration enthalpy).

• If hydration enthalpy > lattice enthalpy → soluble.

• If lattice enthalpy is very large (e.g., MgO), compound may be insoluble despite being ionic.

Overview:

• The Born–Haber cycle is an enthalpy cycle used to calculate or analyse lattice enthalpy by breaking ionic compound formation into separate steps, all of which can be measured or estimated.

• It links atomic processes, electron transfer, and lattice formation to the overall enthalpy of formation (ΔHf°).

---

Example: Sodium chloride (NaCl) formation from Na(s) and Cl₂(g).

Step-by-step process:

1. Sublimation of the metal (ΔHsub)

   • Converts solid Na(s) → Na(g).

   • Endothermic (requires energy to overcome metallic bonding).

2. Ionisation of the metal (Ionisation energy, IE₁)

   • Na(g) → Na⁺(g) + e⁻.

   • Endothermic (energy required to remove an electron from gaseous atom).

3. Dissociation of the non-metal molecule (½ bond enthalpy, ΔHdiss)

   • ½ Cl₂(g) → Cl(g).

   • Endothermic (energy required to break covalent Cl–Cl bond).

4. Electron affinity of the non-metal (EA)

   • Cl(g) + e⁻ → Cl⁻(g).

   • Exothermic (energy released when a gaseous atom gains an electron).

5. Formation of the ionic lattice (Lattice enthalpy, ΔHlatt°)

   • Na⁺(g) + Cl⁻(g) → NaCl(s).

   • Strongly exothermic (large energy release due to strong electrostatic attractions).

---

Cycle equation:

---

Key points for ionic bonding:

• Lattice enthalpy is the biggest single contributor to the stability of an ionic compound — large negative value makes the compound energetically favourable.

• High lattice enthalpy → higher melting point, lower solubility in water (unless hydration enthalpy is larger).

• Comparing lattice enthalpies via Born–Haber cycles explains:

  • Trends in melting points.

  • Stability of ionic solids.

  • Differences between compounds with similar ions but different charges/sizes.

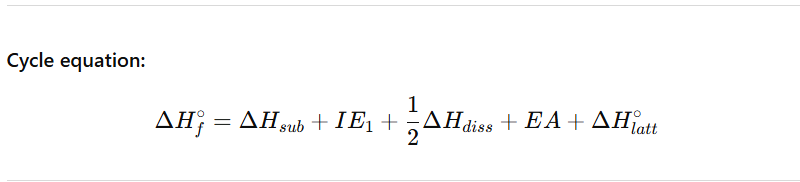
How can you distinguish experimentally between an ionic and a covalent compound?

• Electrical conductivity: Ionic (molten or dissolved) conducts; covalent does not.

• Melting/boiling point: Ionic → high; covalent (simple molecular) → low.

• Solubility: Ionic → soluble in polar solvents; covalent → soluble in non-polar solvents.

• Physical state at room temp: Ionic → solid; covalent → often liquid or gas.