Lens Systems, Thick Lenses

ou will expand your knowledge about refraction to thick lenses and lens systems (e.g., spectacle lenses are thick lenses and the eye and a spectacle lens can be considered a lens system).

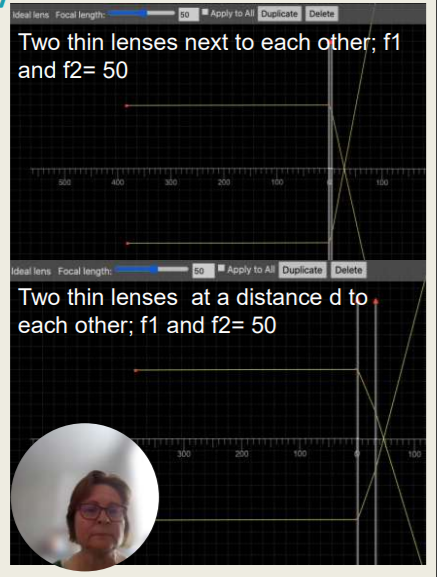
Introduction - Lens System

• The combined power (Fe ) of two thin lenses insignificantly close to each other:

  • F_e = F₁ + F₂

  • Exmaple: F_e = 1/50 + 1/50 and fe =25

  • Light rays focus 2.5 divisions behind lens 2 (see picture)

• If lens 2 is moved a distance (d) away from lens 1, the two parallel light rays focus at a different location behind lens 2:

  • only 1 division instead of 2.5 divisions.

• Implication: the total power F is reduced due to the distance (d) between the lenses

• F = F₁ + F₂ - d x F₁ x F_{2 (equivalent power)}

By moving lens 2 a distance (d) away from lens 1 the _________ is reduced due to the distance (d) between the lenses.

Total power (F)

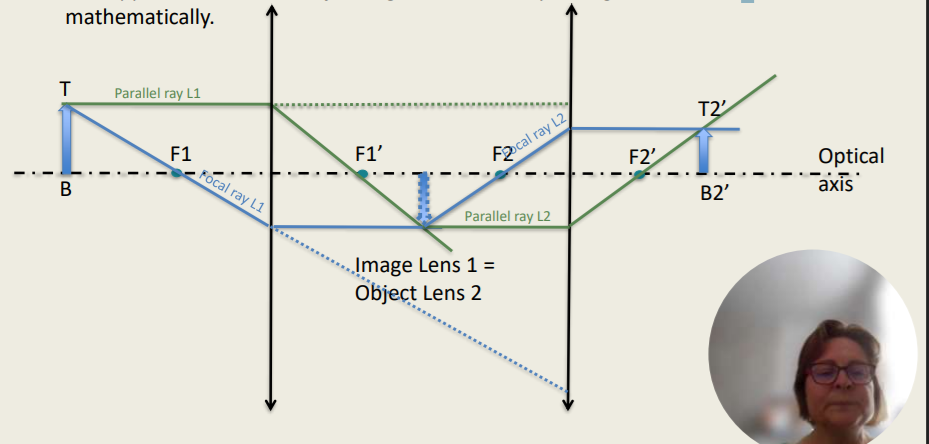
Image Formation Graphically

• How will the image form on a lens system consisting of two lenses:

  • Lens one: The image formed by L1 acts as object for L2

  • Lens 2: final image (B2’T2’) forms behind lens 2 in this case.

• This approach is called “Step-along-method” of raytracing and can also be done mathematically.

The image formed by ______ acts as an object for L2.

L1

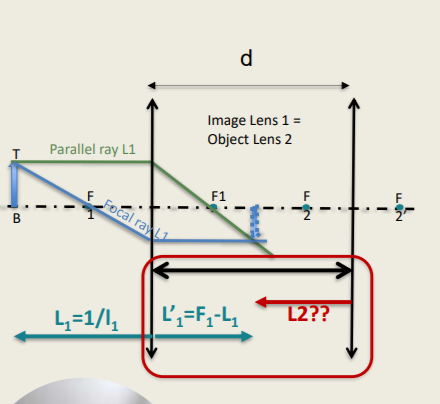
Image Formation Mathematically

The ‘Step-Along’ Method:

• Given L due to object position, annd F1 as F2

• L1’ = F1 + L1

• L1’ serves as object for lens 2 determined by distance (d) between lenses - transition from lens 1 to lens 2.

• We see from picture (directions considered):

• i1’ = i2 + d and this i2 = i1’ - d (convert into equal units!!!)

• Converting into a vergence: 𝑳𝟐 = 𝑳𝟏’ / 𝟏−𝒅 × 𝑳𝟏′ (effective power)

• 𝑳𝟐’ = 𝑭𝟐 + 𝑳𝟐

• Image vergence distance can be calculated then by: 𝑙2’ = 1 / 𝐿 2’

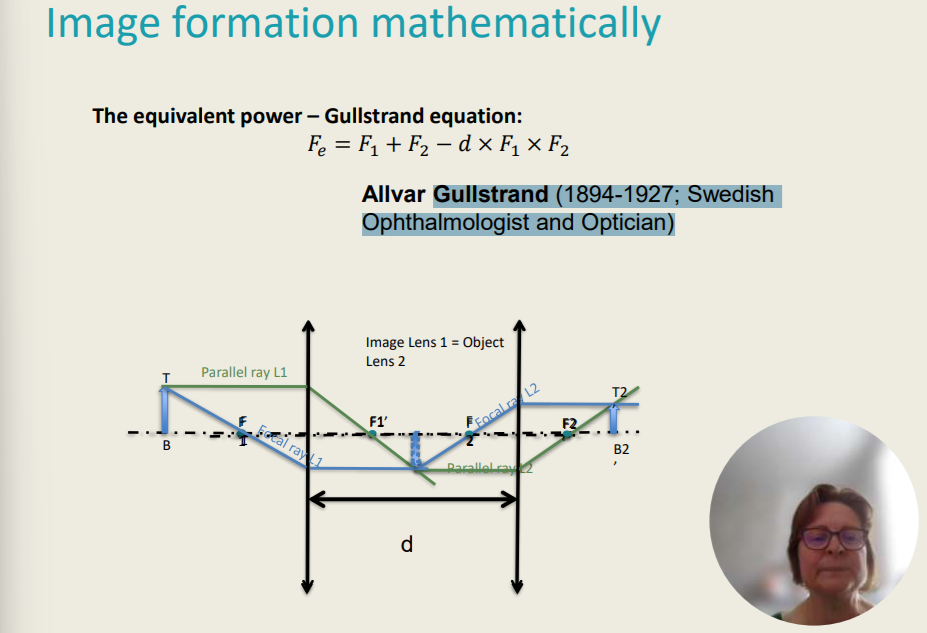
• The equivalent power – Gullstrand equation:

  • 𝐹_𝑒 = 𝐹₁ + 𝐹₂ − 𝑑 × 𝐹₁ × F₂

• Allvar Gullstrand (1894-1927; Swedish Ophthalmologist and Optician)

The equivalent power is the __________.

Gullstrand equation

Combining Two Thin Lenses (1) - System

• By producing the incident parallel ray forwards and the emergent focal ray backwards until they intersect, the system behaves as if it were a single thin lens.

• P’ is called the second principle point and H’P’ the second principle plane. The distance fe ’ is called the second equivalent focal length.

• Thus, to produce a focus at F’, the two lenses F1 and F2 can be replaced by a single lens of equivalent power F’e placed at P’ in the plane H’P’.

• Consider now a light ray emergent from F and passing through the lens system so that the emergent vergence through the system is zero. By producing the emergent ray backwards and the incident ray forwards until they intersect, the system behaves as if it were a single thin lens.

• P is called the first principle point and HP the first principle plane. The distance fe is called the first equivalent focal length.

• Thus, to produce a focus at F, the two lenses F1 and F2 can be replaced by a single lens of equivalent power Fe placed at P in the plane HP.

P’ is called the _____________ and H’P’ is the second principle plane. The distnace fe’ is called the second equivalent focal length.

Second Principle Point

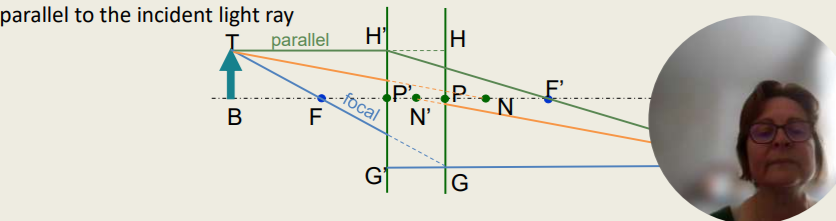
Combining Two Thin Lenses - Nodal Points (3)

• We now trace the rays as done before (on a single lens) through our ‘system’:

• Parallel to the optical axis to second principle plane H’ but leaves the system as if from the plane H’P’ and through F’

• Passes through F to meet the first principle plane H at G leaving the system from G’ parallel to the optical axis

• Directed towards the first nodal point, N and emerges as if from the second nodal point N’, parallel to the incident direction (N and N’ do not coincide with principle planes)

• New: The nodal points, N and N’ are defined as the two points on the principal axis of a lens system such that a ray of light directed towards the first nodal point N, emerges from the system as if it emanated from the second nodal point N’ and in a direction parallel to the incident light ray

The ray passes through ____ to meet the first principle plane H at G leaving the system from G’ parallel to the optical axis.

F

Lens System - Newtons Formula

• The equivalent focal power and focal lengths (first and second) can be calculated as follows:

  • 𝑭𝒆 ′ = 𝟏 / 𝒇𝒆 ′ and 𝐹𝑒 = − 1 / 𝑓𝑒 and 𝒇𝒆 = −𝒇e’

• Objects and images through the lens system are related by Newton’s formula:

  • (f_e’)² = -xx’ or f_ef_e’ = xx’

• Linear magnification, m through the lens system can be calculated as follows:

  • m = h’ / h = - f_e / x = - x’ / f_e’

Objects and images through the lens system are related by ____________.

Newton’s Formula

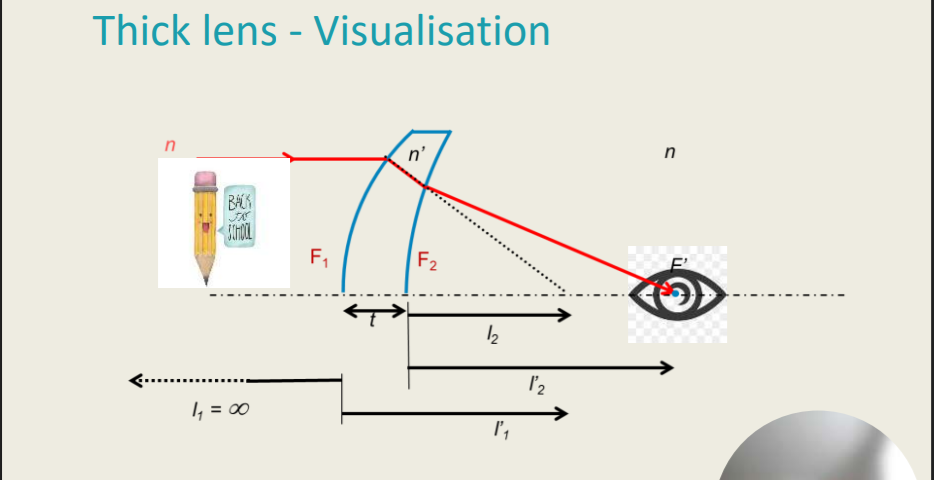
Thick Lenses - The Difference to Thin Lenses

• For thin lenses the power is given by the sum of both surface: 𝑭 = 𝑭𝟏 + 𝑭2 and F can be calculated as follows: F = n / f’

• Example: The focal length of a thin lens in air is 25 cm in front of the lens surface. What is the power of the lens?

  • f’ = - 0.25 m ; n_air = 1

  • Substituting gives 𝑭 = 𝟏 / −𝟎.𝟐𝟓 𝒎 = −𝟒. 𝟎𝟎 𝑫

• A thick lens differs from a thin lens by the centre thickness t and thus F = F1+F2+??

• Application: In spectacle lenses you have a front surface with a front surface radius r₁ and a back surface with a back surface radius r2

A thick lens differs from a thin lens by the _______ and thus F = F1 + F2

Centre Thickness (t)

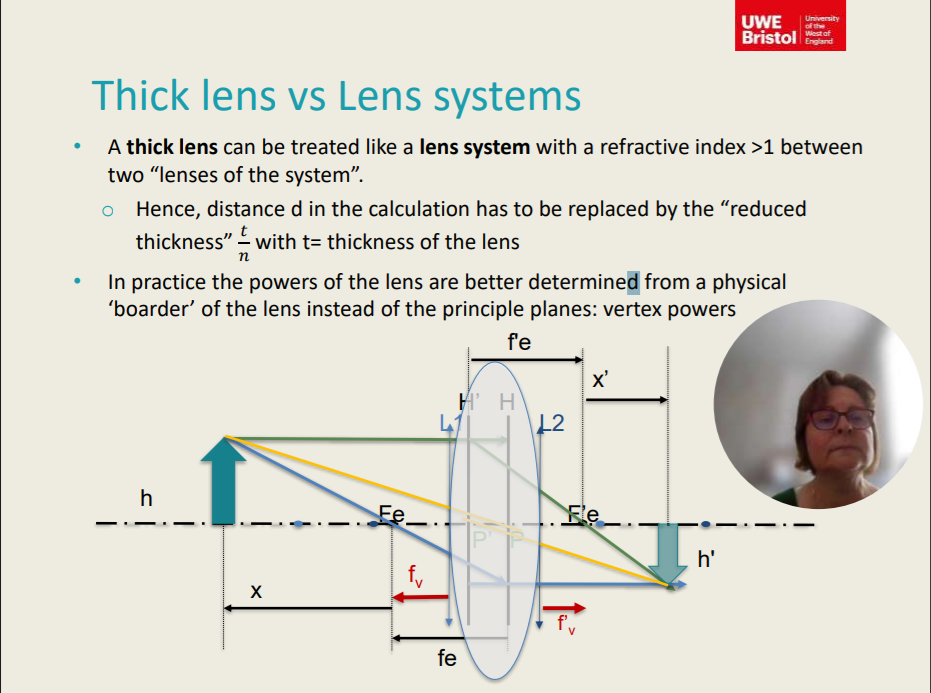
Thick Lens vs Lens Systems

• A thick lens can be treated like a lens system with a refractive index >1 between two “lenses of the system”.

  • Hence, distance d in the calculation has to be replaced by the “reduced thickness” 𝑡 / 𝑛 with t= thickness of the lens

• In practice the powers of the lens are better determined from a physical ‘boarder’ of the lens instead of the principle planes: vertex powers

Distance (d) in the calculation has to be replaced by the ________ t / n with t = thickness of the lens.

Reduced thickness

Spectacle Lenses - Thick Lenses

• For spectacle lenses measurement of the back vertex power or BVP (F’v) is the crucial power value due to representing the power of the lens from the viewpoint of the lens wearer.

• How to derive this equation?

• 𝑭 𝒗’ = 𝑭𝟏 + 𝑭𝟐 − 𝒅 × 𝑭𝟏 × 𝑭𝟐 / 𝟏 − 𝒅 × 𝑭𝟏 𝒘𝒊𝒕𝒉 𝒅 = 𝒕 / n (for FVP)

The _____ is a crucial power value.

Back vertex power (BVP)

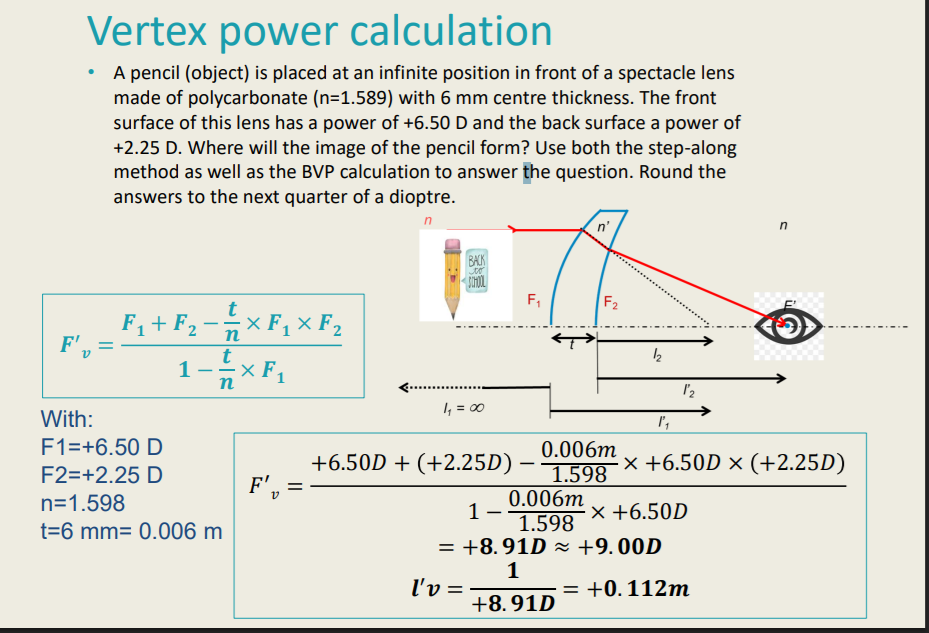
Step- Along Method vs Vertex Power Calculation on Thick Lens

A pencil (object) is placed at an infinite position in front of a spectacle lens made of polycarbonate (n=1.589) with 6 mm centre thickness. The front surface of this lens has a power of +6.50 D and the back surface a power of +2.25 D. Where will the image of the pencil form? Use both the step-along method as well as the BVP calculation to answer the question. Round the answers to the next quarter of a dioptre.

How I Would Calculate This Answer:

Vertex Power Calculation

𝑭 ′ _𝒗 = 𝑭𝟏 + 𝑭𝟐 − 𝒕 / 𝒏 × 𝑭𝟏 × 𝑭𝟐 / 𝟏 − 𝒕 / 𝒏 × 𝑭𝟏

• F1 = +6.50D

• F2 = +2.25D

• n = 1.598

• t = 6mm = 0.006m

𝑭 ′ _𝒗 = +6.50D + +2.25D − 0.006m / 1.598 × (+6.50D) × (+2.25D) / 𝟏 − 0.006m / (1.598) × (+6.50D)

F’_v = +8.91D = +9.00D

I’_v = 1/ (+8.91D) = +0.112m

Step - Along Method

• Surface Power: 𝑭 = 𝑳 ′ − 𝑳

• Incident Vergence: 𝑳 = 𝒏 / 𝒍

• Emergent Vergence: 𝑳′ = 𝒏′ / 𝒍′ Parallel rays (infinite position) have a vergence of “0 D” (L1)

• With:

  • F1 = +6.50D

  • n = 1

  • n’ = 1.589

  • L1 = +0.00D

• Rearrange 𝐹1 = 𝐿 ′1 − 𝐿1 for L’1: 𝐿 ′1 = 𝐹1 + 𝐿1

• 𝐿 ′1 = +6.50𝐷 + 0.00𝐷 = +6.50D

• Rearrange 𝐿 ′1 = 𝑛 ′ / 𝑙 ′1 for l’1: 𝑙 ′1 = 𝑛 ′ / 𝐿 ′1

• 𝑙 ′1 = 1.598 / +6.50𝐷 = +0.246m

Transition S1 > S2

• Surface Power: 𝑭 = 𝑳 ′ − 𝑳

• Incident Vergence: 𝑳𝟐 = 𝒏 / 𝒍𝟐

• Emergent Vergence: 𝑳 ′ = 𝒏′ / 𝒍 ′

• Parallel rays (infinite position) have a vergence of “0 D”

• 𝑙 ′1 = 1.598 / +6.50𝐷 = +0.246𝑚

• Image l’1 serves as object for 2nd surface: 𝑙2 = 𝑙 ′1 − 𝑑

• 𝑙2 = +0.246𝑚 − 0.006𝑚 = +0.24𝑚

• 𝐿2 = 𝑛 / 𝑙2 = 1.598 +0.24𝑚 = +6.66D

• Rearrange 𝐹2 = 𝐿 ′2 − 𝐿2 for L’2: 𝐿 ′2 = 𝐹2 + 𝐿2

• 𝐿 ′2 = +2.25𝐷 + +6.66𝐷 = +8.91𝐷

• Rearrange 𝑳 ′𝟐 = 𝒏′ / 𝒍 ′𝟐 for l’2: 𝒍 ′𝟐 = 𝒏′ / 𝑳 ′𝟐

• 𝒍 ′𝟐 = 𝟏 / +𝟖.𝟗𝟏𝑫 = +𝟎. 𝟏𝟏𝟐m

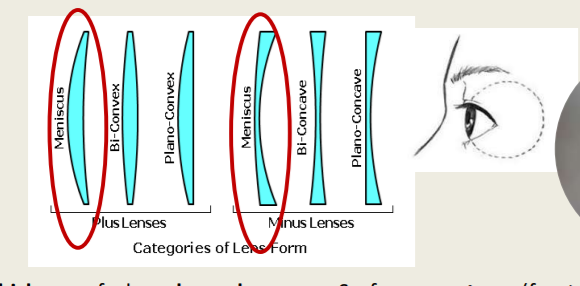
Thickness Calculation Spectacle Lenses

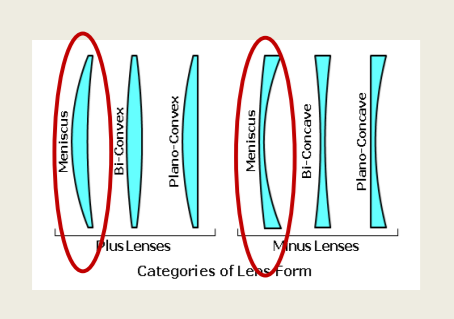
• Spectacle lenses have a distinct combination of curvatures: they are called “meniscus” (meaning: concave back surface).

• The thickness of a lens depends upon …. Surface curvatures (front and back), size of the lens (determined by frame) and lens material (n determines refraction)

Lens thickness depends on the ________ , size of the lens (frame dependent) and the lens material (n determines refraction).

Surface of Curvatures (front and back)

Why is Thickness of a Spectacle Lens of Importance?

• Spectacle lenses should be sufficiently robust, whilst being thin as possible to maintain a good cosmetic appearance.

• Since most lenses possess spherical (circular) curves, the thickness of a lens can be calculated by measuring the curve drop of the surface from the chord limiting the diameter of the surface

The lens thickness can be calculated by measuring the ___________ from the chord limiting the diameter of the surface.

Curve Drop of the Surface

Calculating Centre - and Edge Thickness of Spectacle Lenses

• using saggita (s) (meaning: the height of a segment of a circle sphere”)

• 𝑠 = 𝑦² ×𝐹 / 2000 × (𝑛′−𝑛) with

  • s = saggita/sag in mm

  • y = half the lens diameter in mm

  • F = surface power (front surface of lens)

  • n’ = refractive index second medium (lens)

  • n = refractive index first medium (air)

• Knowing “s” allows to calculate centre thickness in positive lenses and edge thickness of negative lenses, but also the power of the surface.

________ is the height of a segment of a _________.

Saggita; Circle Sphere

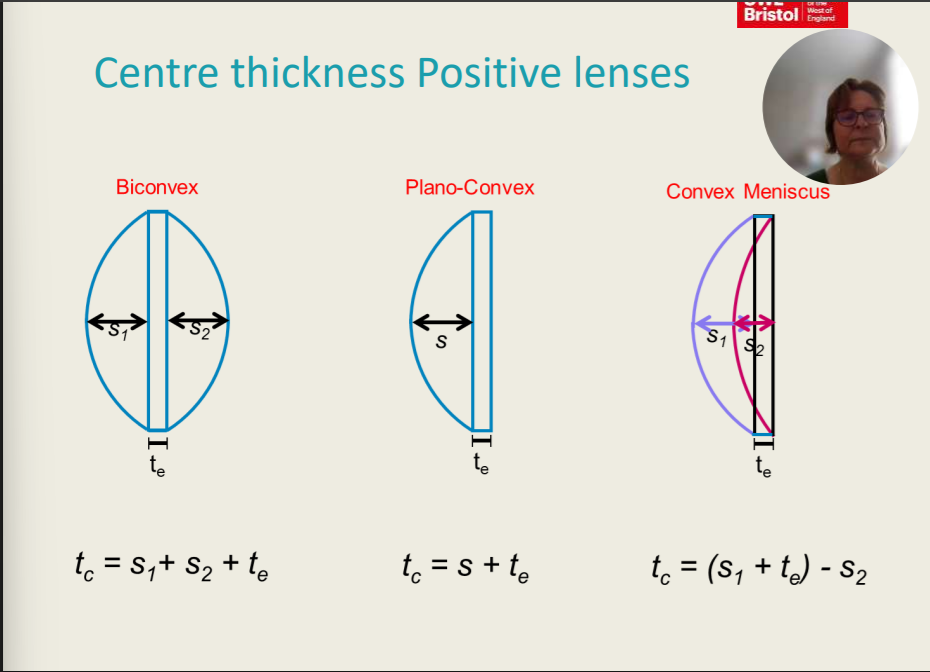
Centre Thickness Positive Lenses

• Biconvex

  • t_c = S₁ + S₂ + t_e

• Plano-convex

  • t_c = s + t_e

• Convex Meniscus

  • t_c = (S₁ + t_e) - S₂

The _____ types of positive lenses are biconvex lenses, convex meniscus lenses, and plano- convex lenses.

Three

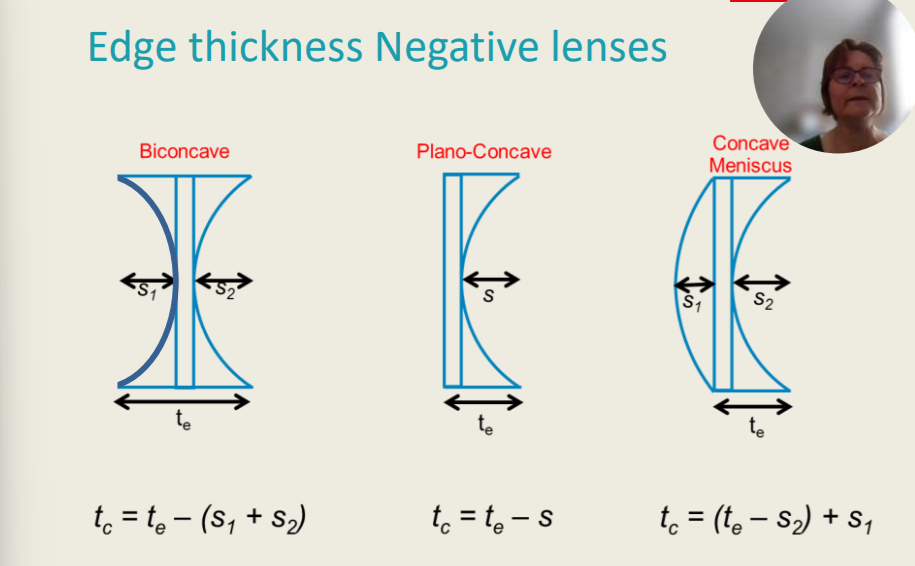
Edge Thickness Negative Lenses

• Biconcave

  • t_c = t_e - (S₁ + S₂ )

• Concave Meniscus

  • t_c = t_e - S

• Plano-Concave

  • t_c = (t_e - S₂) + S₁

There are _____ types of negative lenses which are biconcave, plano-concave and concave meniscus lenses.

Three

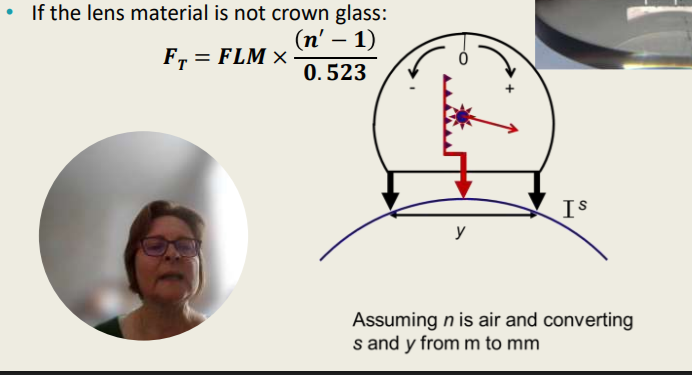
The Surface Power

• The lens measure is a practical application of this principle: It measures the surface power of a lens by applying the sag-equation.

• Lens measures are calibrated for crown glass (n’=1.523)

• If the lens material is not crown glass:

  • FT = FLM x (n’ - 1) / 0.523

  • Assuming n is air and converting s and y from m to mm

The _______ can measure the surface power of the lens and the lens measures are calibrated for _________ with a refractive index of _______.

Sag-Equation; Crown Glass; 1.523

Lens Thickness Calculation

Calculate the edge thickness of a -10.00DS spectacle lens made in meniscus form from crown glass. The surface powers of the lens are +4.00DS (front surface) and -14.00DS (back surface). The spectacle lens has a centre thickness of 1mm and a lens diameter of 44mm. Please round the result to two decimals.

How to Calculate the Answer:

• Minus-lens, Meniscus

• F1 = +4.00D

• F2 = -14.00D

• tc = 1mm

• Dia = 44mm → y = 22mm

• n = 1.523

• Lens Thickness Calculation - S1

  • 𝑠 = 𝑦² ×𝐹 2000 × (𝑛′−𝑛) with n’=n in second medium and n=>n in first medium; F in D and s, y in mm;

  • s needs to be calculated at both surfaces at the lens! 𝑡𝑐 = (𝑡𝑒 − 𝑠2) + 𝑠1 (needs rearranging for te)

  • 𝑠1 = 𝑦² × 𝐹1 / 2000 × (𝑛 ′ − 𝑛) = 22𝑚𝑚² × (+4.00𝐷) / 2000 × (1.523 − 1) = +1.85𝑚m

• Lens Thickness Calculation - S2

• 𝑠1 = 𝑦² × 𝐹1 / 2000 × (𝑛 ′ − 𝑛) = 22𝑚𝑚² × (-14.00𝐷) / 2000 × (1 - 1.523) = +6.48

• Lens Thickness Calculation - T_e

• 𝑡_𝑐 = (𝑡𝑒 − 𝑠2) + 𝑠1 (needs rearranging for te)

• Rearranging:

  • –s1: 𝑡𝑐 − 𝑠1 = (𝑡𝑒 − 𝑠2)

  • +s2: 𝑡𝑐 − 𝑠₁ + 𝑠2 = 𝑡e

• Calculation:

  • 1𝑚𝑚 − 1.85𝑚𝑚 + 6.48𝑚𝑚 = 𝑡𝑒 = 5.63𝑚m

Need to Know:

• Read the notes of the image.

Centre- and edge- thickness of _______ can be calculated from the sagg-equation s= = 𝑦² ×𝐹 / 2000 × (𝑛′−𝑛)

Thick Lenses

Think for yourself

Try to see if you can answer this from the seminar.