FBS Geometry • Postulates

Segment Addition Postulate (Seg. Add. Post.)

the parts = the whole
AB + BC = AC

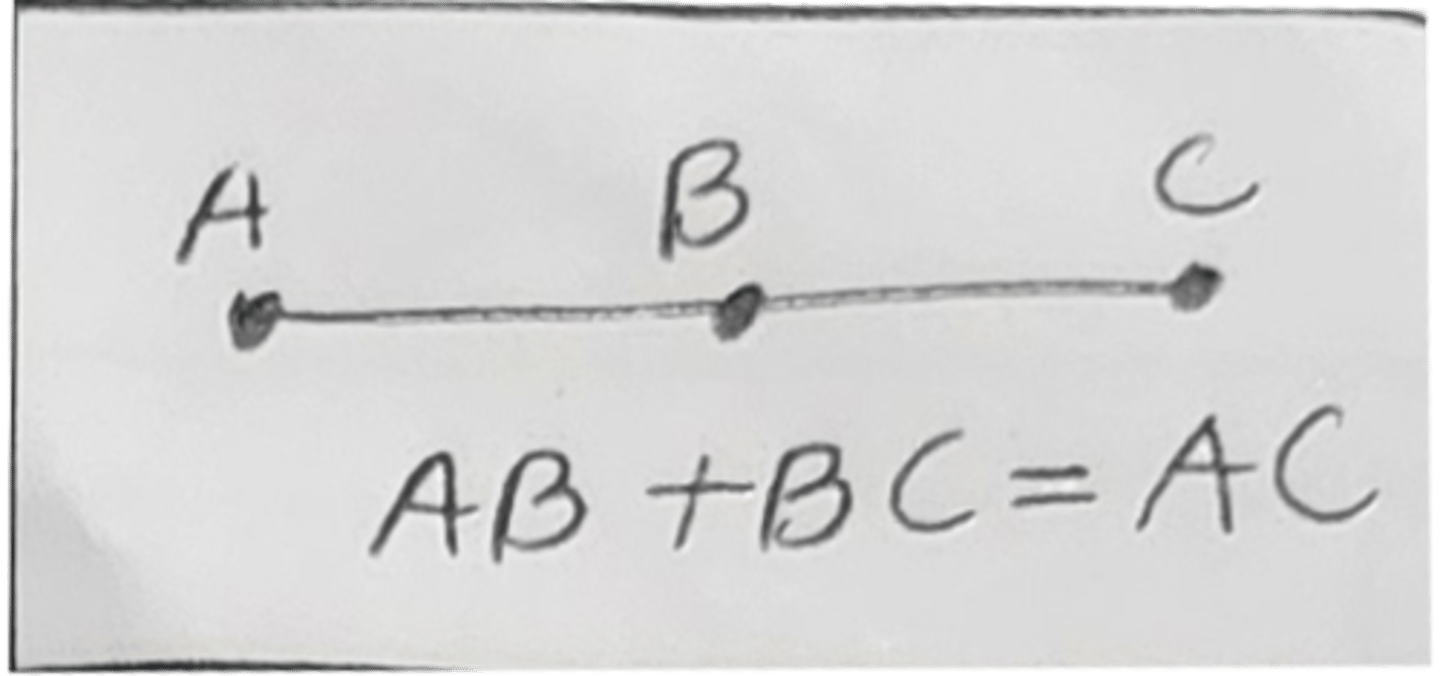
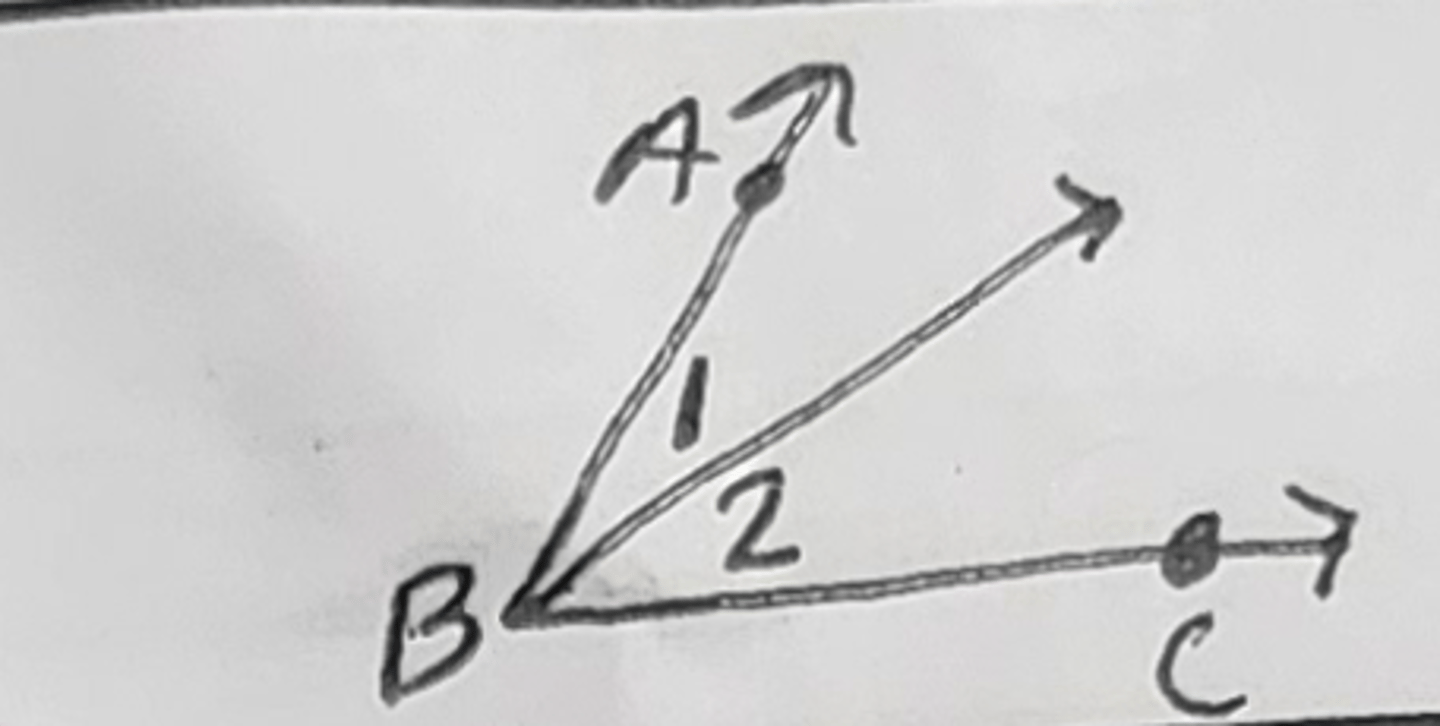
Angle Addition Postulate (< Add. Post.)

the parts = the whole
<1 + <2 = <ABC

Addition Property of Equality (Add. Prop. of = OR + prop of =)

when you add the same thing to both sides

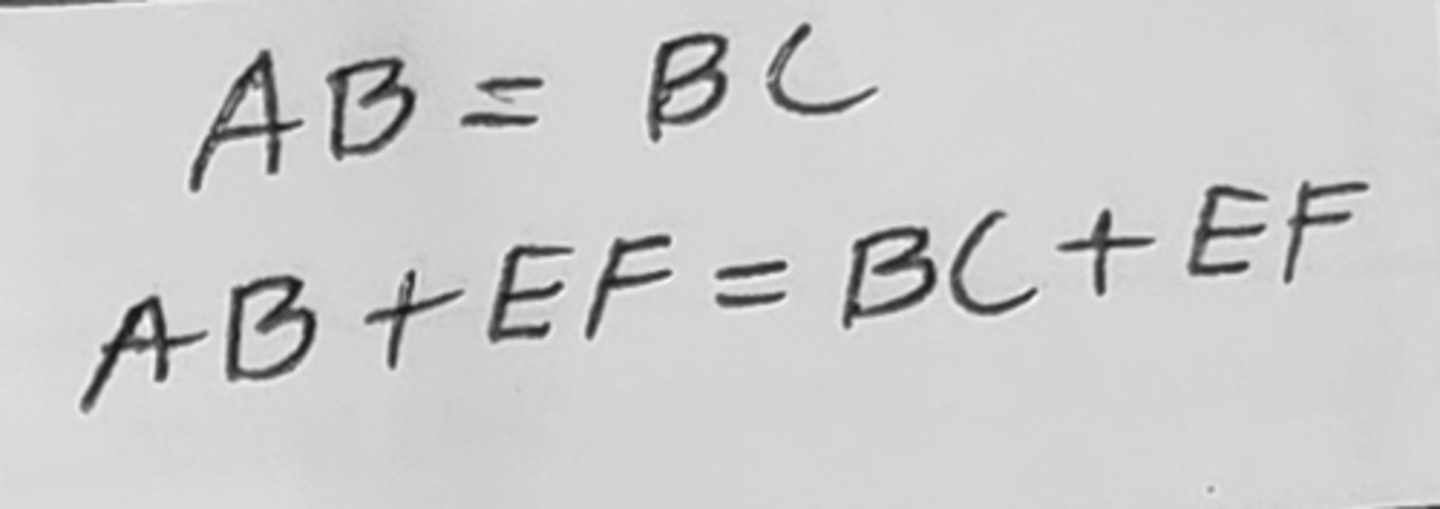
Subtraction Property of Equality (Sub. Prop. of = OR - prop of =)

when you subtract the same thing to both sides

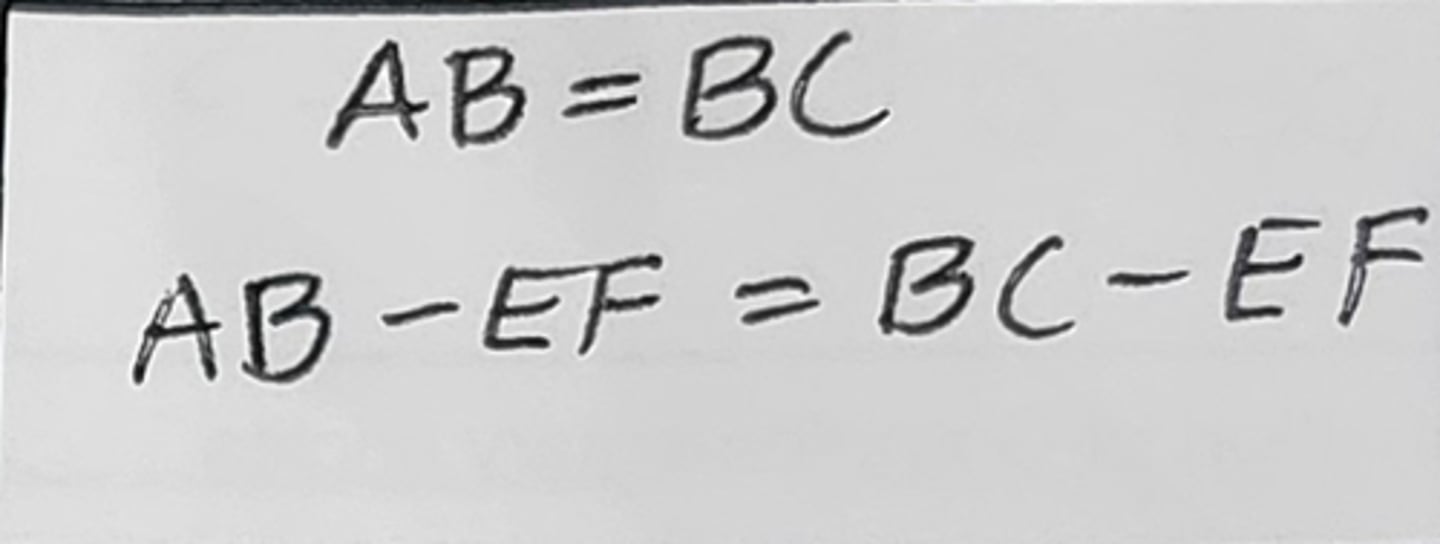
Multiplication Property of Equality (Mult. Prop. of = OR X prop of =)

when you multiply the same thing to both sides

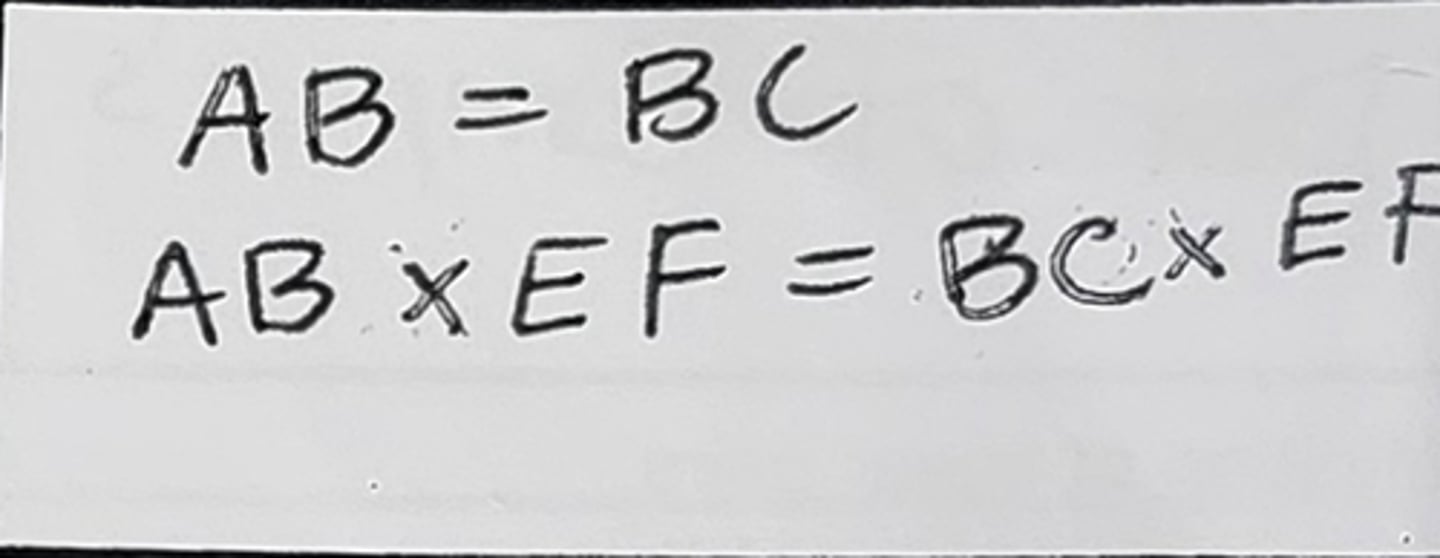
Division Property of Equality (Div. Prop. of = OR ÷ prop of =)

when you divide the same thing to both sides

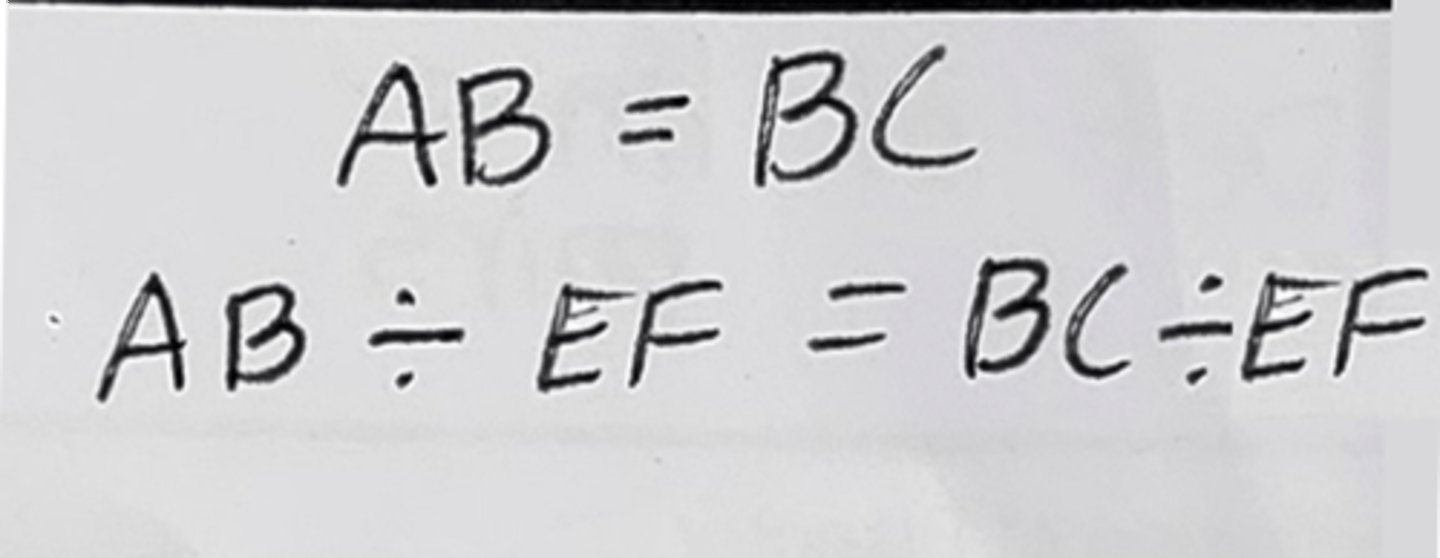
Substitution Property of Equality (Subs Prop of =)

when you substitute/replace something in an equation

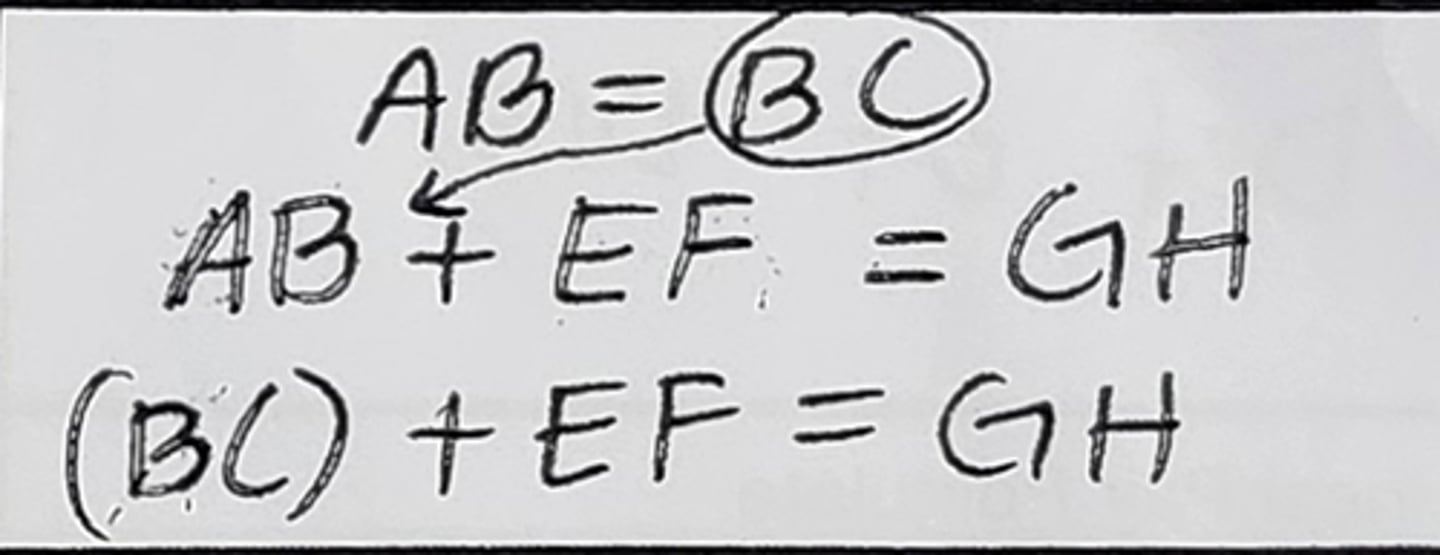
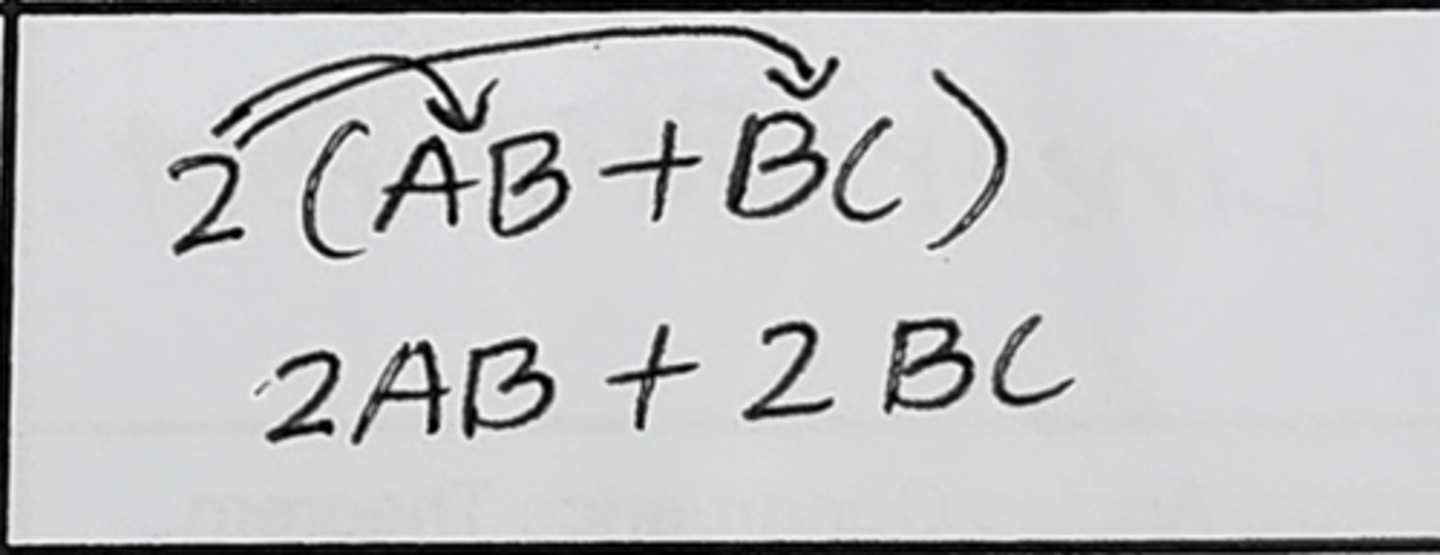
Distributive Property of Equality (simplify) (Distr. Prop. of =)

when you distribute/multiply something to a group of numbers

Reflexive Property of Equality (Reflex Prop of =)

Reflection

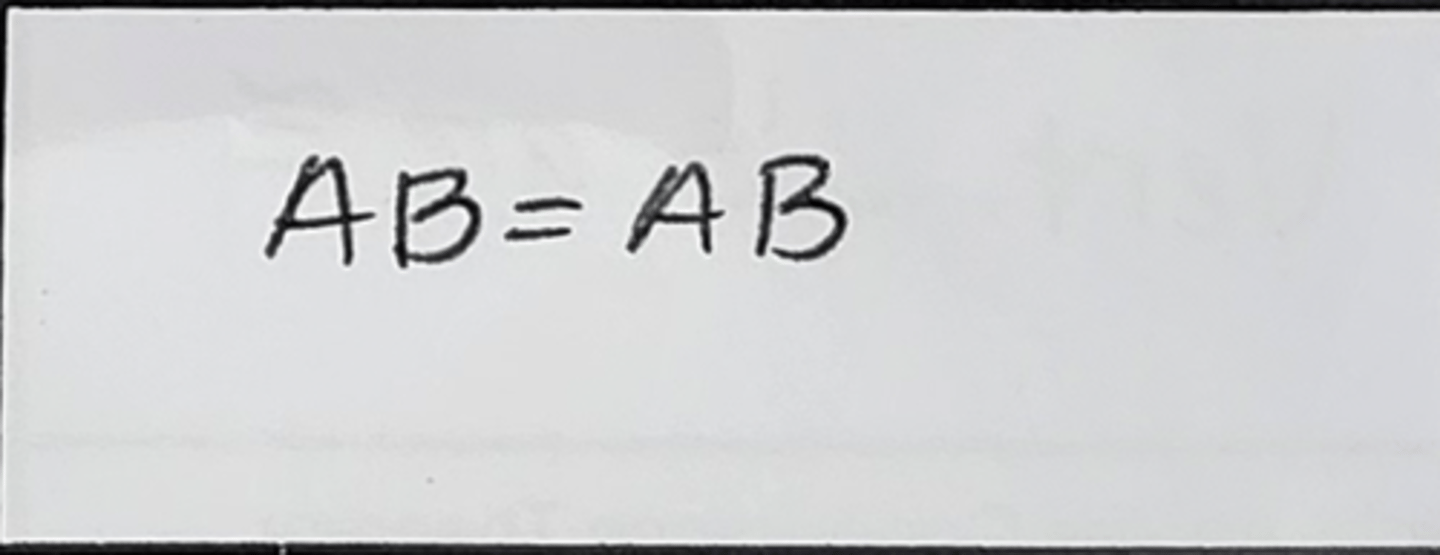
Symmetric Property of Equality (Sym Prop of =)

Switch

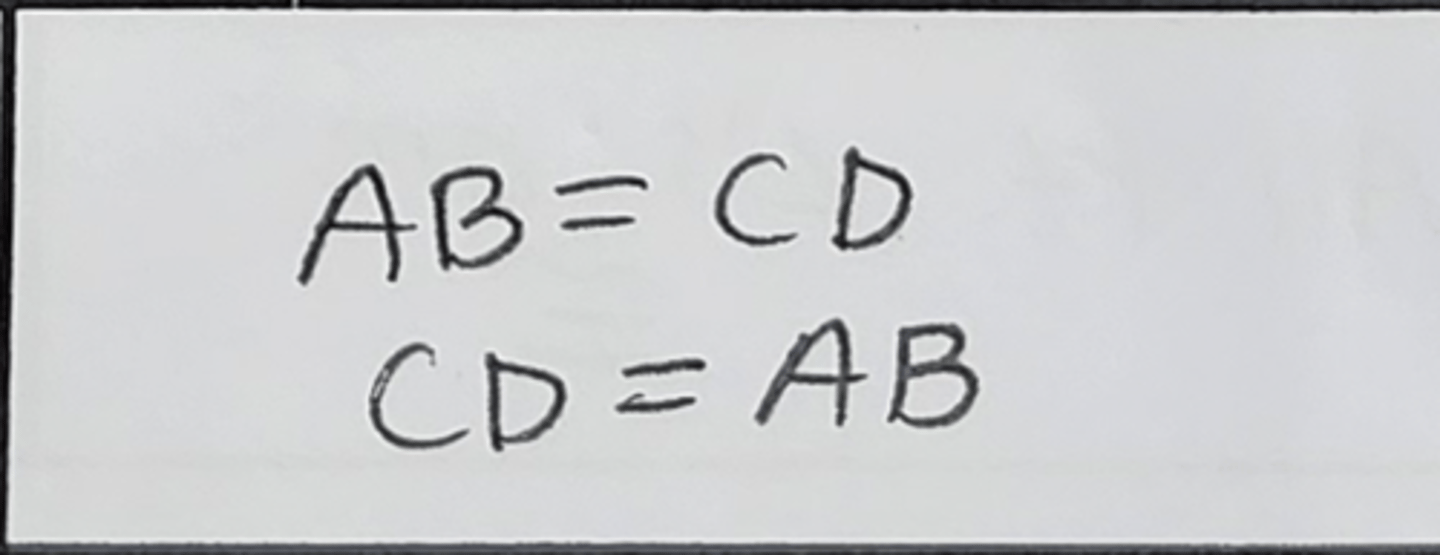
Transitive Property of Equality (Trans Prop of =)

need a connection

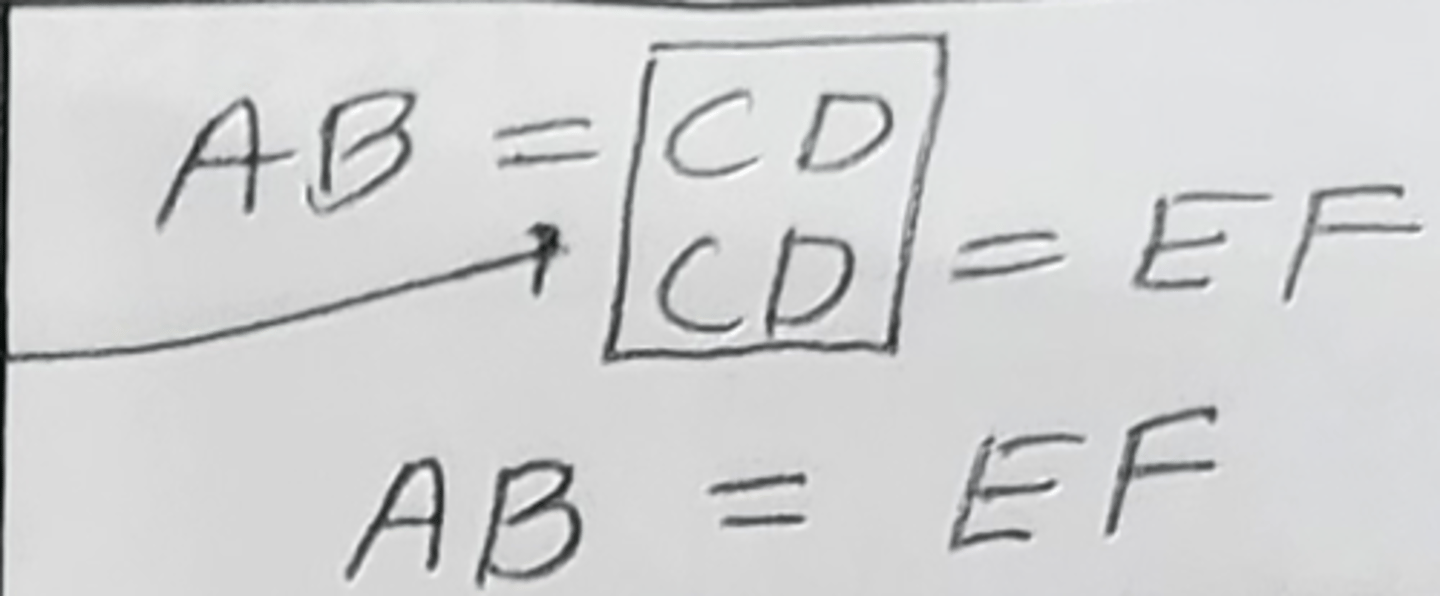
Definition of Midpoint (def of midpoint)

a point that gives 2 equal parts

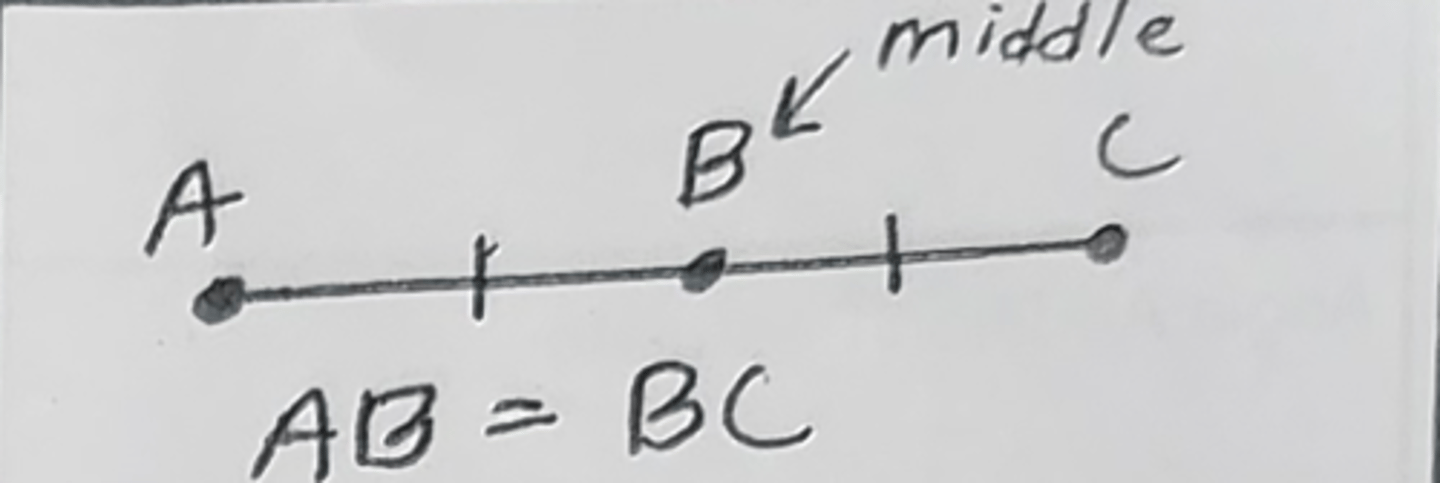
Definition of Congruence (Def. of ~=)

congruent to equal
equal to congruent

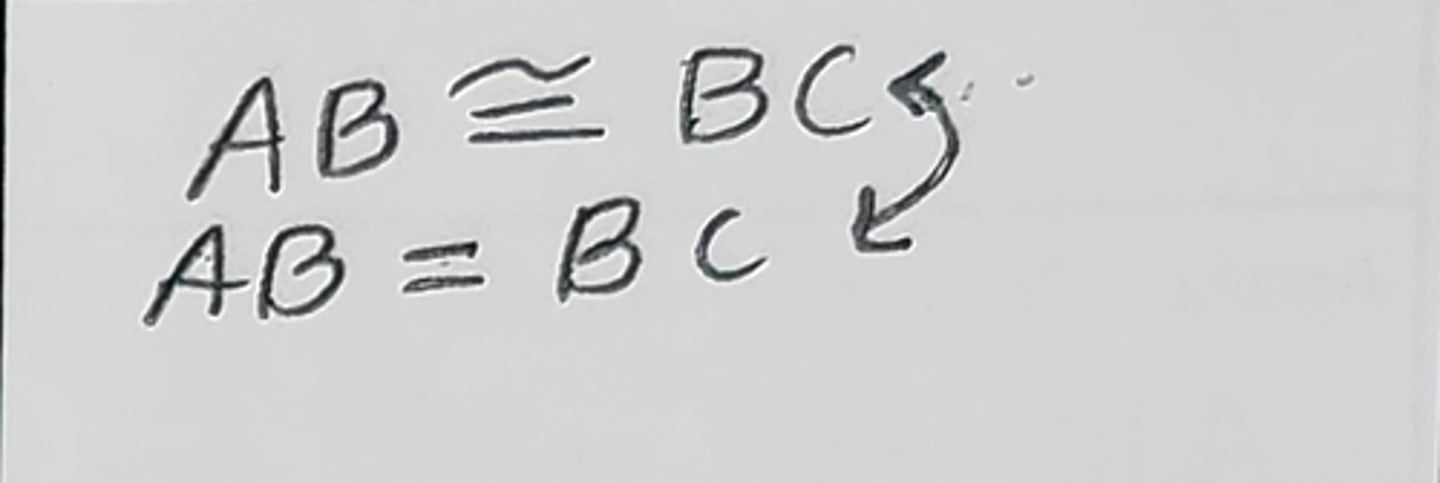
Definition of Supplementary Angles (Def of Supp <'s)

2 <'s that add up to 180°

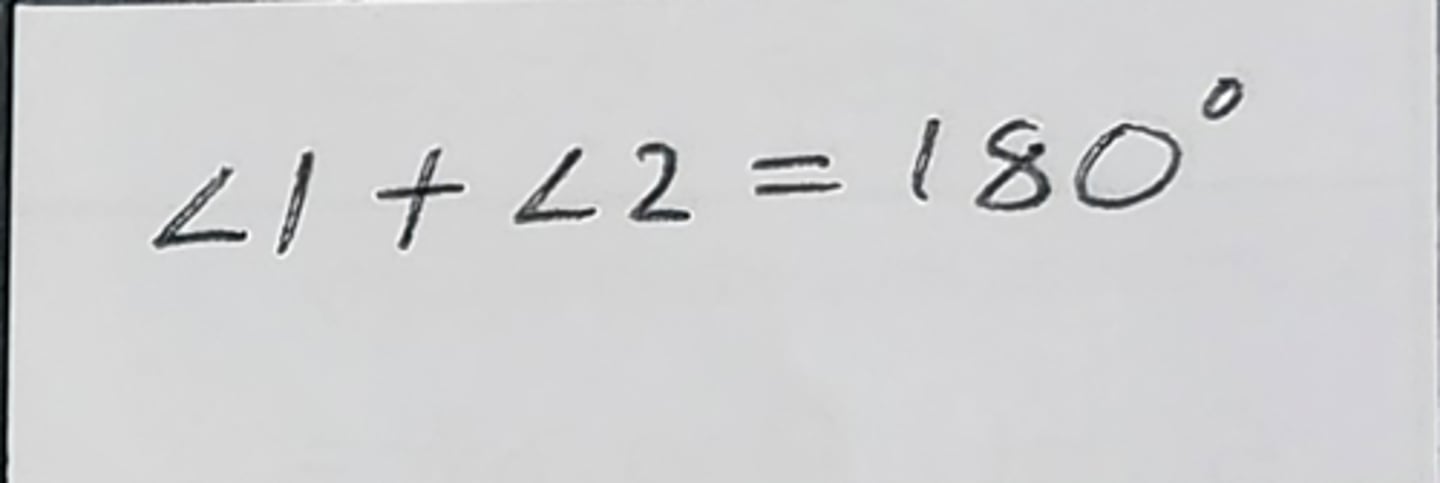
Definition of Complementary Angles (Def of Comp <'s)

2 <'s that add up to 90°

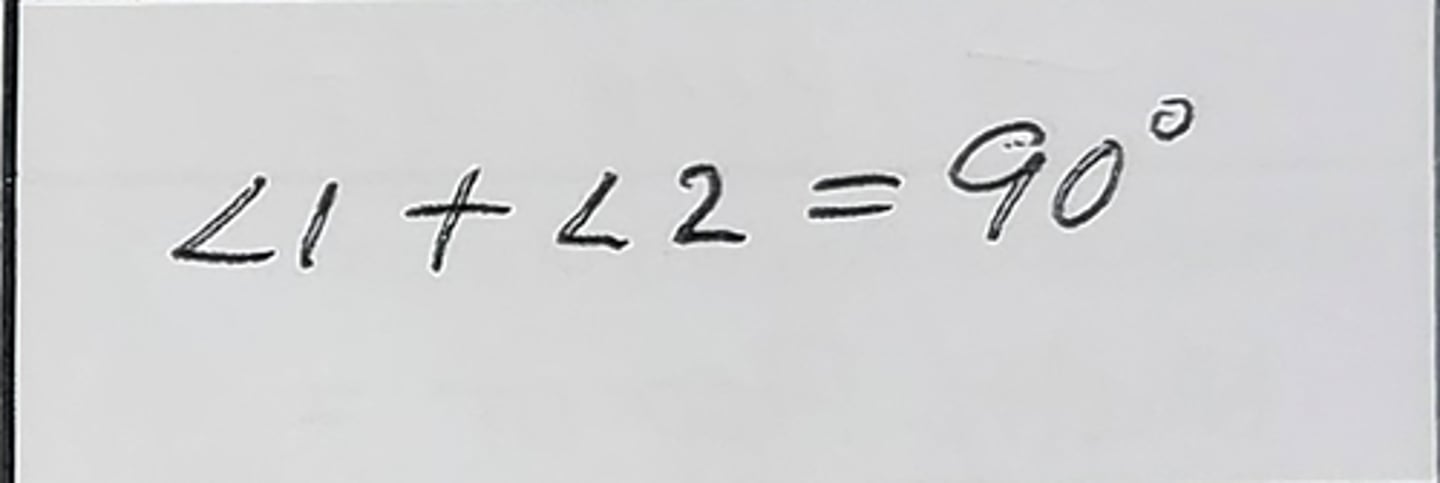
Definition of Linear Pairs (Def of linear pairs)

2 adjacent angles that make a straight line

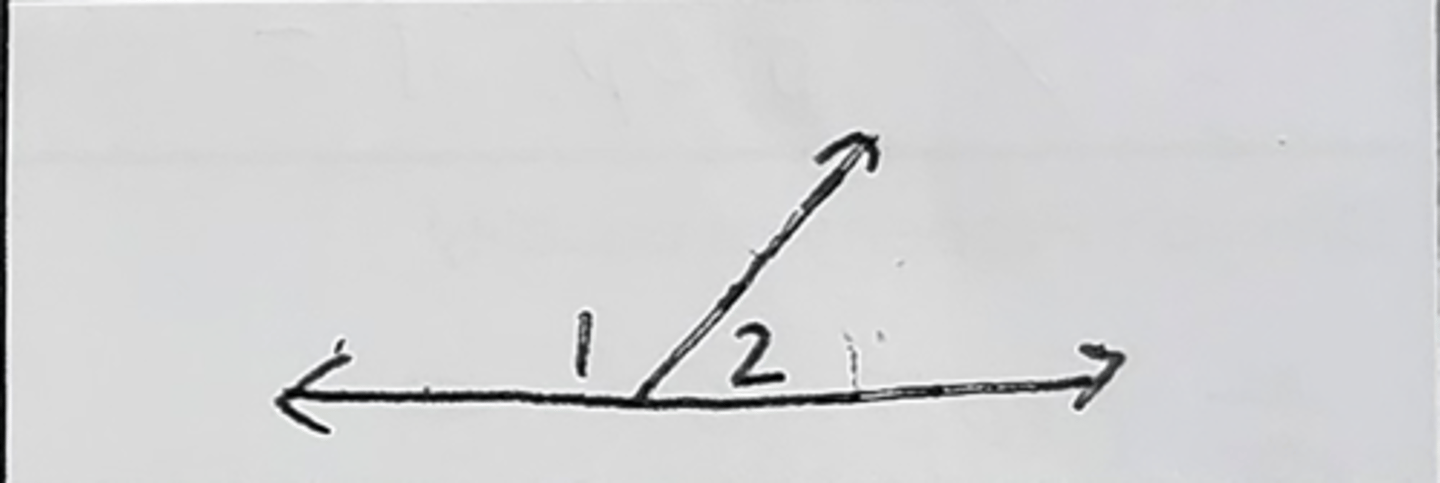
Definition of Bisector (Def of Bis)

a line, ray, or segment that gives two equal parts

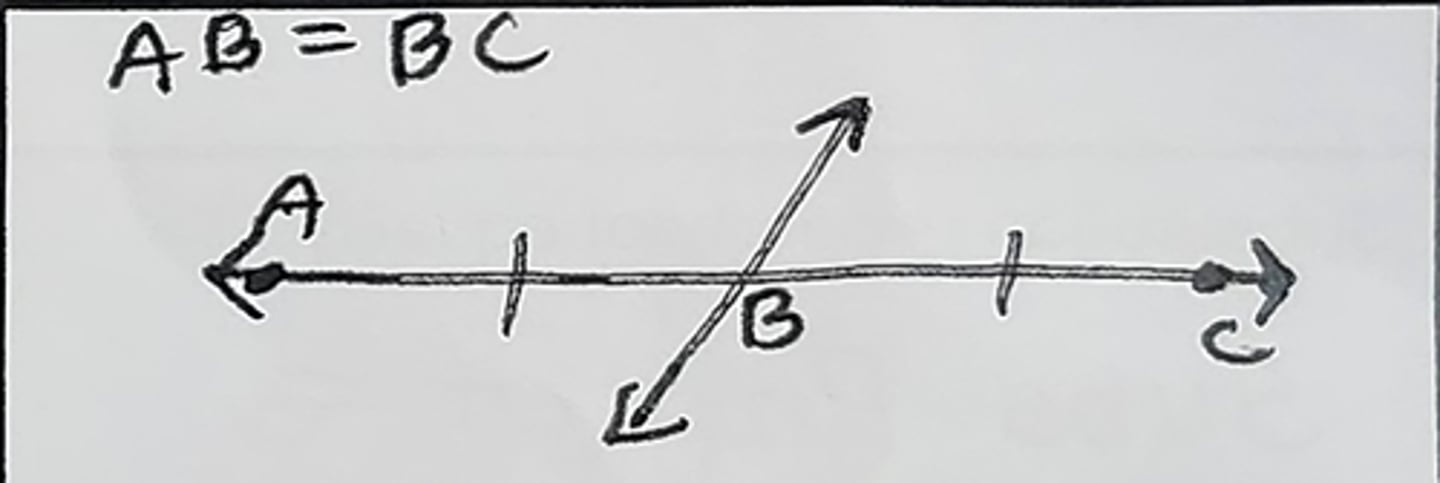
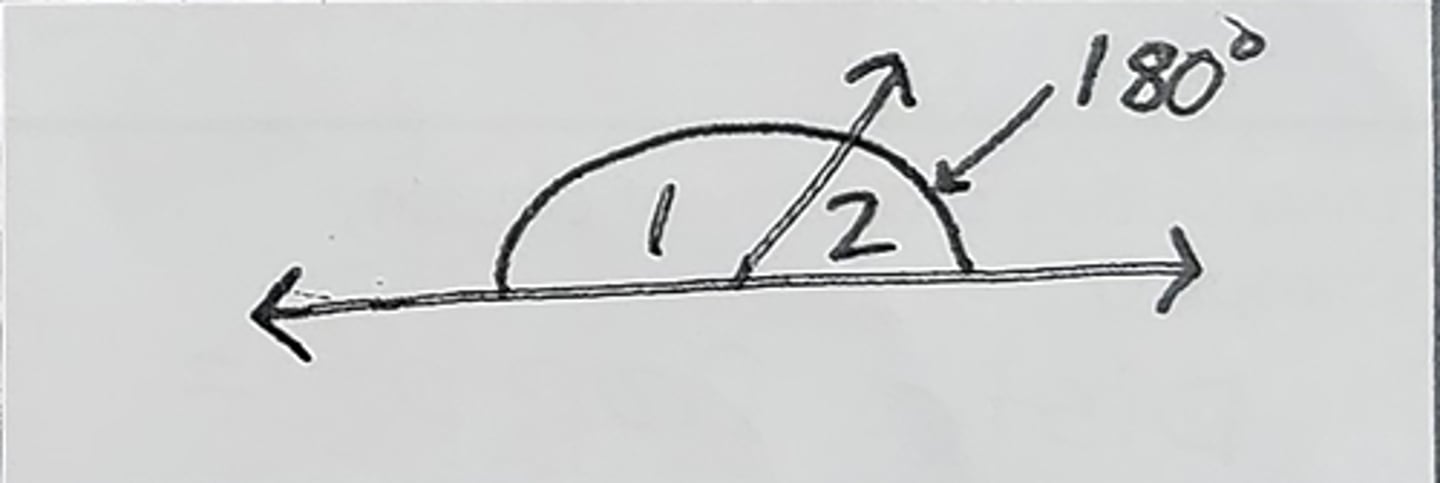
Linear Pair Postulate (Linear Pair Post)

Linear Pairs are supplementary = to 180°

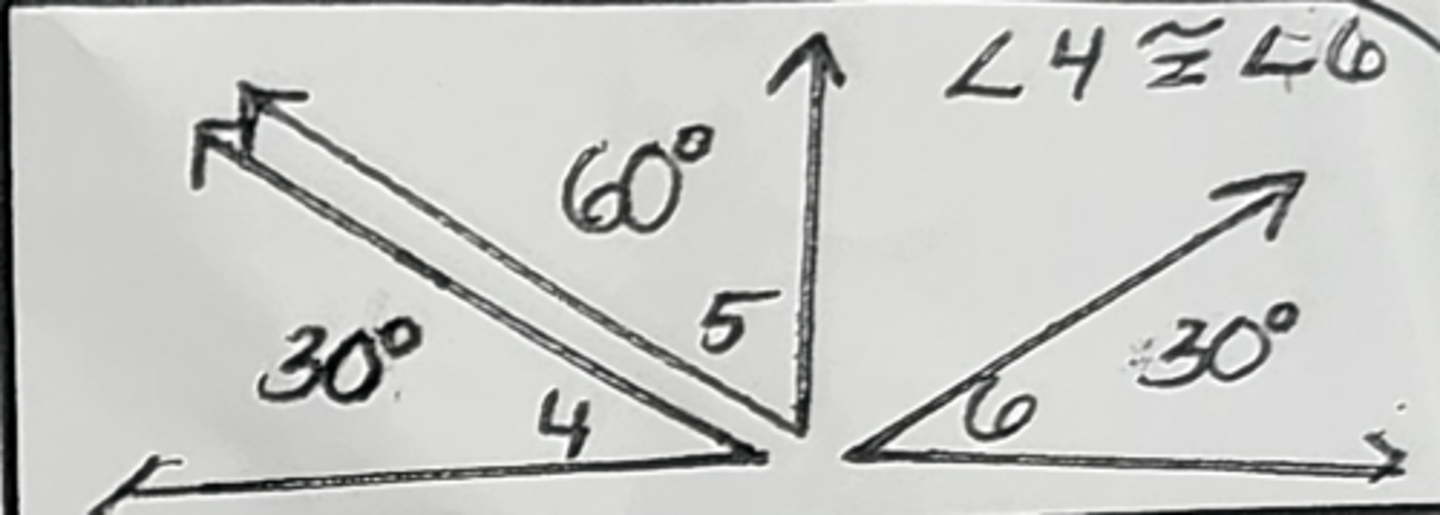
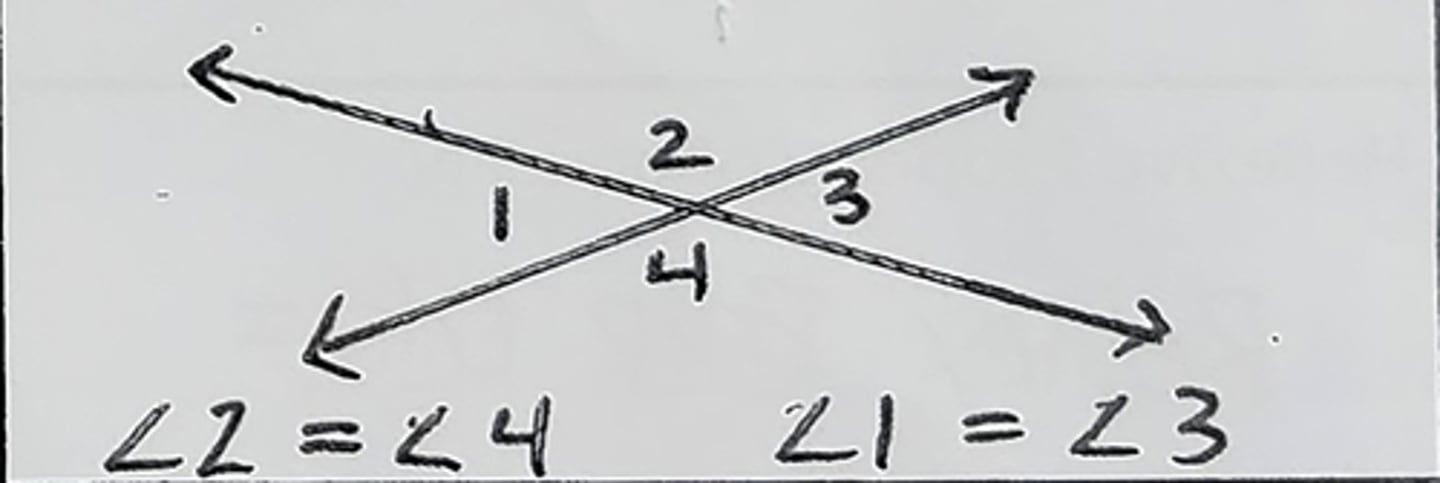
Vertical Angles Congruence Theorem (Vert <'s are ~=)

Vertical <'s are ~=

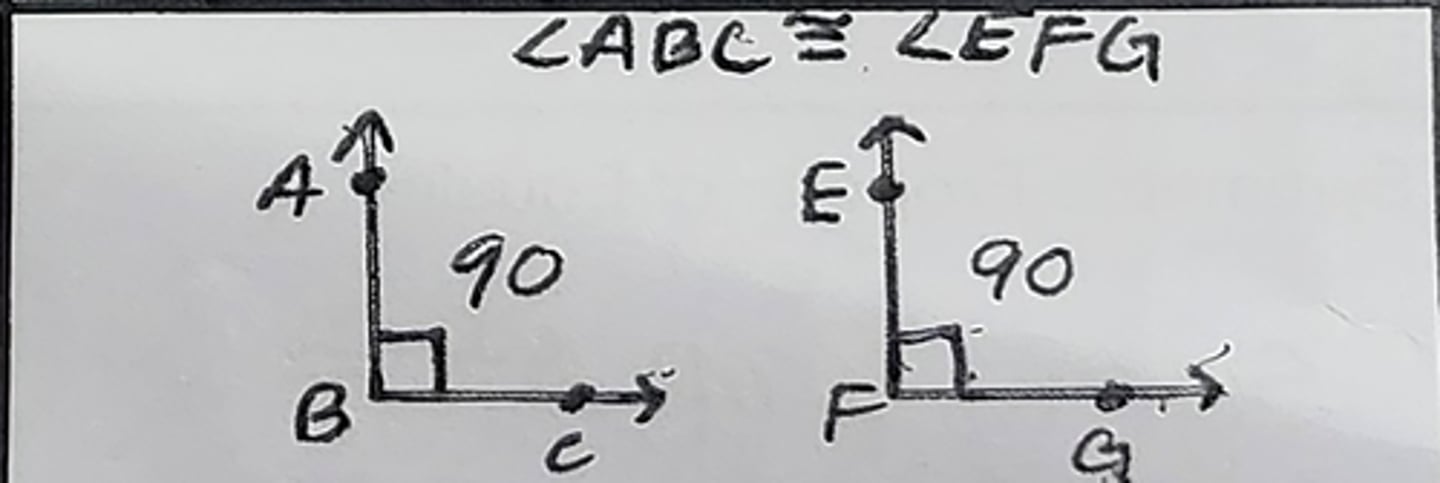
Right Angles Congruence Theorem (All rt. <'s are ~=)

Right <'s are ~= to each other

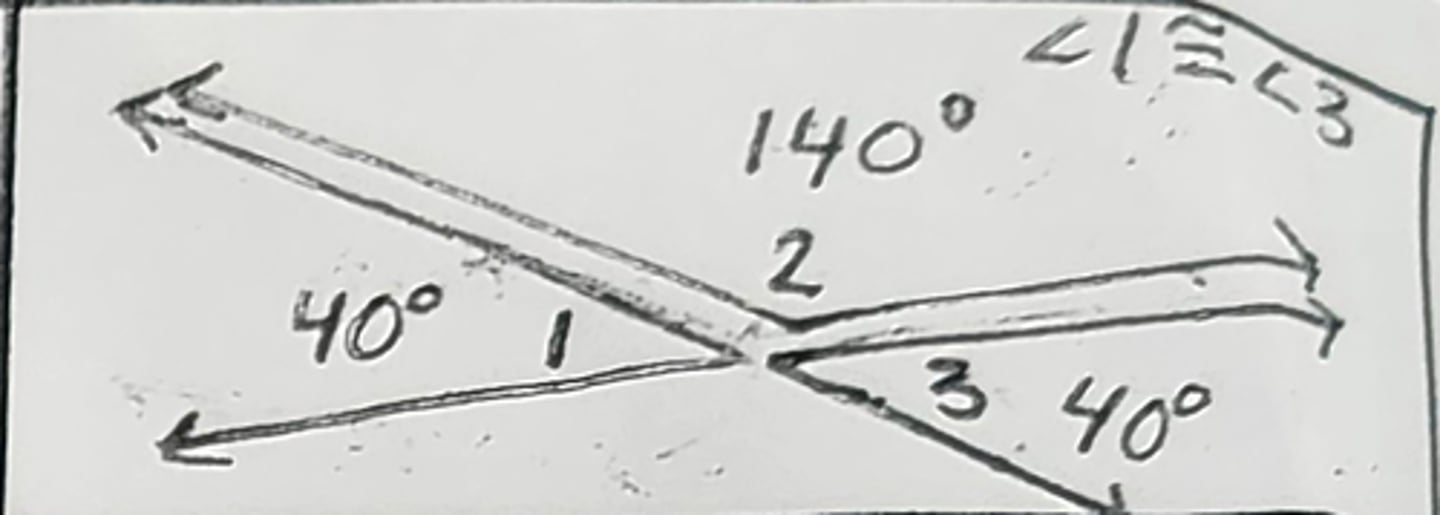
Congruent Supplements Theorem (~= Supp Thm)

2 <'s supplementary to the same < are congruent/equal

Congruent Complements Theorem (~= Comp Thm)

2 <'s complementary to the same < are congruent/equal