LESSON 13: Chi-Square Statistic, Test for Goodness of Fit and Independence

Parametric

make assumptions about the parameters of the population distribution from which the sample is drawn

Nonparametric

not based on assumptions, that is, the data can be collected from a sample that does not follow a specific distribution

Chi-Square (χ² )

statistical test used to examine the differences categorical variables from a random sample to judge the goodness of fit between expected and observed.

True

True or False

unlike the other variables we have tested, we cannot describe our data for the χ² test using means and standard deviations. Instead, we will use frequencies tables.

False

True or False

like the other variables we have tested, we can describe our data for the χ² test using means and standard deviations. we will not use frequencies tables.

True

True or False

Chi-square (χ² ) test - assumes that each observation comes from only one person and that each person will provide only one observation, so our total observations will always equal our sample size

False

True or False

chi-square (χ² ) test - assumes that each observation comes from only two people and that each person will provide only two observations, so our total observations will not always equal our sample size.

Expected Value

what would be found if each category had equal representation

N

the total number of people in our sample

C

the number of categories in our variable

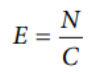
the calculation for an expected value is:

Test for Goodness Fit

assesses one categorical variable against a null hypothesis of equally sized frequencies.

Null Hypothesis

For χ² tests for goodness of fit, our ___ is that there is an equal number of observations in each category. there is no difference between the categories in how prevalent they are

Alternative Hypothesis

our _ says that the categories do differ in their frequency 

True

True or False

we do not have specific directions or one-tailed tests for χ² , matching our lack of mathematical statements.

True

True or False

our degrees of freedom for the χ² test are based on the number of categories we have in our variable

not on the number of people or observations like it was for our other test

False

True or False

our degrees of freedom for the χ² test are not based on the number of categories we have in our variable, it is based on the number of people or observations like it was for our other test.

True

True or False

DEGREES OF FREEDOM AND THE χ² TABLE

our degrees of freedom, along with our significance level (still defaulted to α = .05) are used to find our critical values in the χ² table

False

DEGREES OF FREEDOM AND THE χ² TABLE

our degrees of freedom, along with our significance level (still defaulted to α = .05) are not used to find our critical values in the χ² table.

True

True or False

because we do not have directional hypotheses for χ² test. we do not need to differentiate between critical values for one- or two-tailed tests.

In fact, just like our F test for regression and ANOVA, all χ² tests are one-tailed tests.

False

True or False

because we have directional hypotheses for χ² test. we need to differentiate between critical values for one- or two-tailed tests. in fact, just like our F test for regression and ANOVA, all χ² tests are two-tailed tests.

True

True or False

EFFECT SIZE FOR χ² 

there are many options for which effect size to use, and the ultimate decision is based on:

• the type of data

• the structure of your frequency or contingency table

• the types of conclusions you would like to draw.

Cramer’s V

type of correlation coefficient that can be computed on categorical data.

like any other correlation coefficient (e.g., Pearson’s r), the cutoffs for small, medium, and large effect sizes of Cramer’s V are .10, .30, and .50, respectively.

True

HYPOTHESIS TESTING  IN CHI-SQUARE

True or False

for this calculation, k is the smaller value of either R (the number of rows) or C (the number of columns).

The numerator is simply the test statistic we calculate during Step 3 of the hypothesis-testing procedure.

True

CONTINGENCY TABLES FOR TWO VARIABLES

True or False

the test for goodness of fit is a useful tool for assessing a single categorical variable.

However, what is more common is wanting to know if two categorical variables are related to one another.

False

CONTINGENCY TABLES FOR TWO VARIABLES

True or False

the test for goodness of fit is not a useful tool for assessing a single categorical variable. However, what is more unusual is wanting to know if two categorical variables are not related to one another.

True

CONTINGENCY TABLES FOR TWO VARIABLES

True or False

this type of analysis is similar to a correlation, the only difference being that we are working with nominal data, which violates the assumptions of traditional correlation coefficients.

False

CONTINGENCY TABLES FOR TWO VARIABLES

this type of analysis is not similar to a correlation, the only similarity being that we are working with nominal data, which doesn’t violate the assumptions of traditional correlation coefficients.

Contingency Table

shows the frequency of each category in one variable, contingent upon the specific level of the other variable.

True

True or False

In contrast to the frequency table for our test for goodness of fit, our contingency table does not contain expected values, only observed data.

False

True or False

In contrast to the frequency table for our test for goodness of fit, our contingency table contains expected values, not only observed data.

Marginal Values

the total values for a single category of one variable added up across levels of the other variable.

True

True or False

the marginal values for rows and columns will always both add up to the total number of participants, N, in the study.

If they do not, then a calculation error was made and you must go back and check your work.

True

True or False

our expected values for contingency tables are based on the same logic as they were for frequency tables,

but now we must incorporate information about how frequently each row and column was observed (the marginal values) and how many people were in the sample overall (N) to find what random chance would have made the frequencies out to be

Test for Independence

the χ² test performed on contingency tables

• used to see if the values of each categorical variable (the frequency of their levels) are related to or independent of the values of the other categorical variable

Null Hypothesis

the actual interpretations of the hypotheses are quite simple: the _ _says that the variables are independent or not related

Alternative Hypothesis

the actual interpretations of the hypotheses are quite simple: and the _ says that they are not independent or that they are related