IB Physics SL (Topic A)

Bidwell boys, core concepts from Kognity

Scalar Quantity

A physical quantity that has only magnitude, such as temperature or mass, without direction.

Vector Quantity

A physical quantity that has both magnitude and direction, such as velocity or force.

Methods for Adding Vectors

head-to-tail method, parallelogram method, graphical representation, algebraic addition.

Understand Basic Trig you Noob

SOHCAHTOA

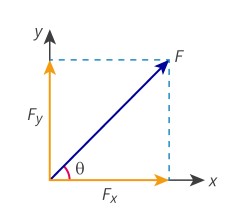
Resolving a Vector

Ax = Acosθ; Ay = Asin θ, where Ax and Ay are the components of the vector A.

position

The placement of an object is given in relation to a reference point.

displacement

A change in position. It is a vector quantity. displacement = final position - initial position

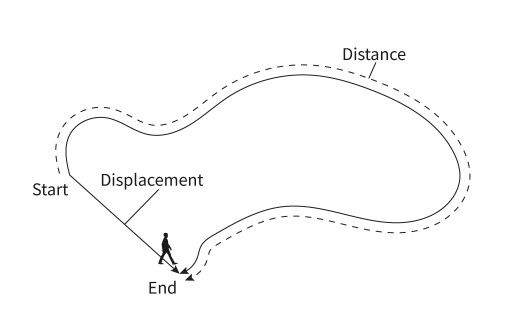
distance

The length of the path followed. It is a scalar quantity. Can never be negative, direction of motion is not important

Velocity

Speed in a specified direction. Velocity is a vector quantity. Rate of change of position.

Velocity (m/s^-1) = change in position/change in time

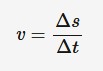
Speed

The rate of change of distance measured in m/s. Speed is a scalar quantity.
speed = distance travelled/change in time

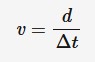
Acceleration

The rate of change of velocity. A vector quantity.
Acceleration = change in velocity/change in time

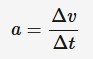
Instantaneous vs average values

average velocity = change in position/change in time
instantaneous velocity = velocity at a specific instance in time

SUVAT EQUATIONS

refer to physics data booklet
v = u + at
s = [(u + v)/2] * t
s = ut + (1/2)at²
v² = u² + 2as

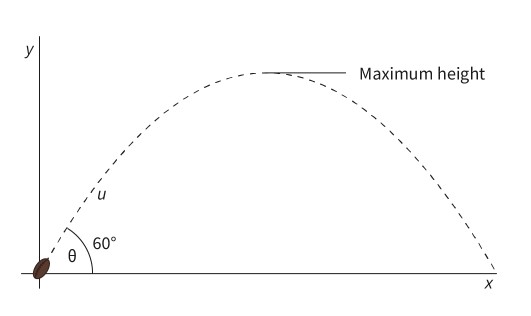
Projectile Motion

We must resolve it in both the vertical and horizontal direction (see section A.1.1) using the equations of motion (see section A.1.3).

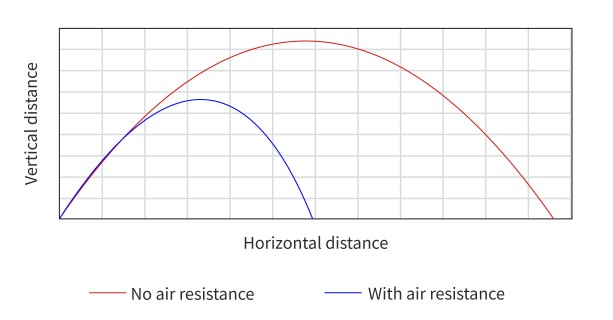
Effect of Fluid Resistance on a Projectile

• The trajectory is a different shape (it is not parabolic).

• The maximum height is lower.

• The range is shorter.

• The velocity of the object will be lower due to the effect of air resistance decreasing the acceleration of the object.

• An object experiencing air resistance travelling upwards will reach its maximum height sooner, so the time of flight when going up is less.

• An object experiencing air resistance travelling downwards will experience an upwards air resistance, so the time of flight when going down is greater.

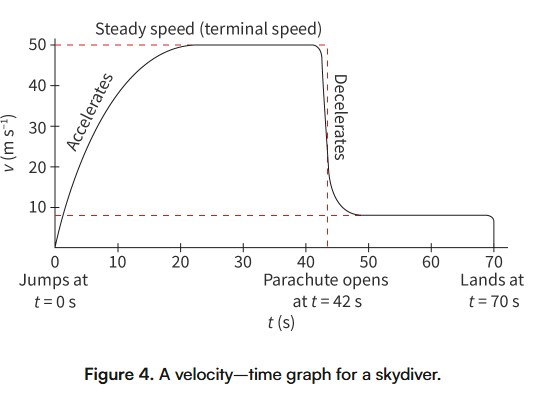
terminal speed

The top speed reached by any object experiencing air resistance or a similar resistance force.
EX: As the skydiver is moving downwards, air is pushing upwards. The faster the person falls, the greater the air resistance, and the smaller the acceleration. Eventually, the acceleration becomes zero and the speed is constant.

Uniform Motion

Motion with a constant velocity

Uniformly accelerated motion

motion with a constant acceleration

Force

An interaction between bodies that can change the motion of a body, or change the shape or size of a body. Vector quantity, measure in newtons (N), need two or more bodies involved.

When you analyze forces, you need to be able to

• resolve force vectors into components.

• add forces as vectors

Free-Body diagram

to simplify problems in physics, we draw a diagram that shows the forces on the body we are interested in.

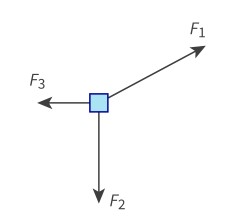
Resultant force

The vector sum of all the forces acting on an object. The resultant force is the single force that can replace all the individual forces acting on a body.

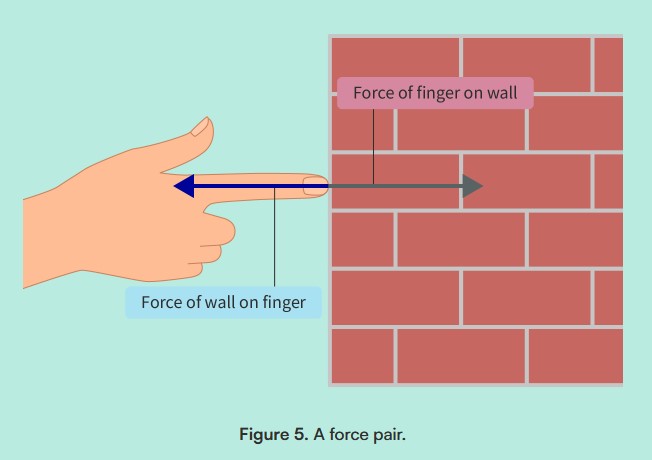
Newton’s third law of motion

For every action (force) there is an equal and opposite reaction (force).

Fields

• A region of space where a particle experiences a force. Examples include an electric field, magnetic field and a gravitational field.

• explains how forces can act at a distance

gravitational force

• All bodies with mass exert a gravitational force on other bodies.

• The direction of the gravitational force is toward the centre of the Earth.

• gravitational force = mass * gravity (9.8)

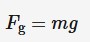
weight

The pull of gravity on a body, measured in newtons (N).

non-contact forces vs contact forces

non-contact forces = the two bodies do not need to be touching for them to exert a force on each other

contact forces = the two bodies need to be touching for a force to act

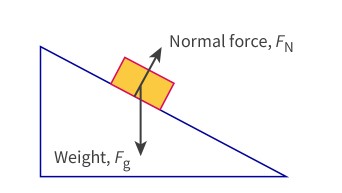
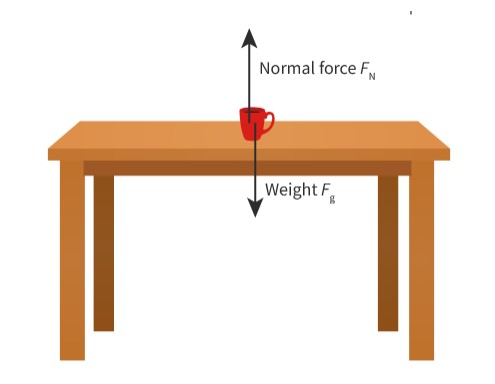
Normal Force

The contact force that acts on a body that is perpendicular to the surface in contact with the body. Measured in Newtons

Frictional force

• A force between two surfaces when in contact. It impedes motion and results in heating.

• It acts in a direction parallel to the plane of contact between the body and the surface.

Static friction

• The frictional force that acts between two bodies rest.

• the force you exert overcomes static friction and the box starts moving along the floor.

• Frictional Force <= (coefficient of static friction) * (normal force)

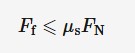
dynamic friction

• The frictional force that acts between two bodies moving relative to each other.

• While the box is moving on the floor, there is still a frictional force between the box and floor that resists the motion.

• Frictional force (newtons) = (coefficient of dynamic friction) * (normal force [newtons])

maximum static friction

• The object is initially stationary. Static friction increases as the applied force increases, up to maximum value. This is called the maximum static friction or threshold of motion. At this point, the object starts to move. The static friction decreases and stabilises at a fixed value of dynamic friction.

• The frictional force needed to keep a body at rest is greater than the frictional force needed to oppose the motion of the body.

• Static friction depends on the magnitude of the applied force, while dynamic friction does not depend on the magnitude of the applied force.

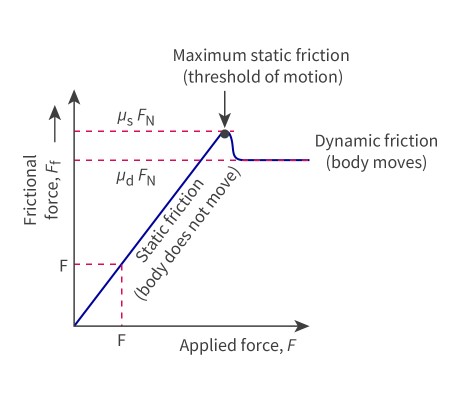
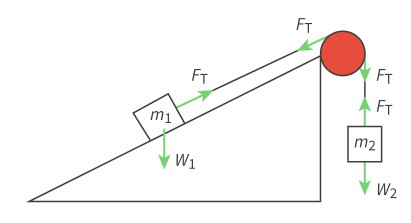
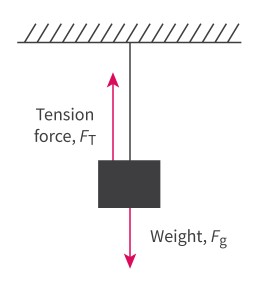
tension force

• It has the same magnitude but opposite direction to the applied force

• The tension force acts along the length of the rope – it pulls the roof of the cave down and the climber up.

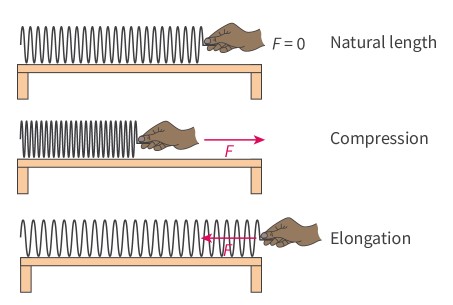
elastic restoring force

The force that counteracts the force extending or compressing a spring and restores the spring to its natural length.

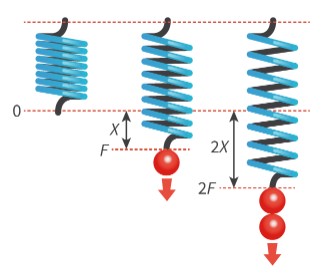
Hooke’s law

• The displacement of a spring is directly proportional to the force exerted on the spring.

• the restoring force acting to return a spring to its length is proportional to the extension of the spring.

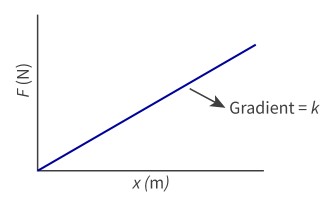
Equation for elastic restoring force

• elastic restoring force(newtons) = -(spring constant[newtons per metre]) * (displacement of spring)

• The minus sign in the equation above tells us that the direction of the elastic restoring force, F_H, is opposite to the direction of the displacement, x.

Viscous drag force

• The resistive force opposing the motion of a body inside a fluid.

• The particles of the fluid exert a force on the surface of the body, opposing its motion.

• depends on viscosity of fluid, property of fluid that describes resistance to flow.

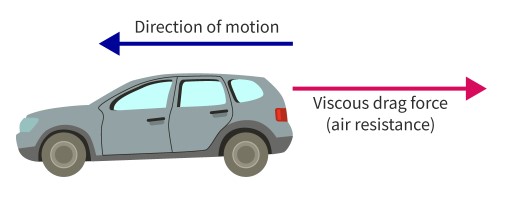
Equation for viscous drag force

• viscous drag force (newtons) = 6pi*(fluid viscosity[kilograms per metre per second]) (radius of sphere[metres])*(velocity of sphere)

Buoyancy

• The force exerted by a fluid on an object partly or wholly immersed in the fluid, that counteracts the weight of the body.

• caused by difference in pressure between top and bottom of a body

• buoyancy experienced by a body is equal to the weight of the fluid displaced

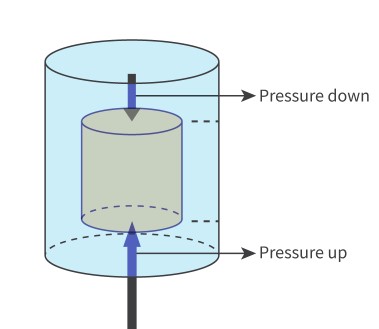
Equation for buoyancy

Fb = buoyancy (Newtons)

p = density of fluid (kg/m³)

V = volume of fluid displaced (m³)

g = gravity

Remember buoyancy is equal to the weight of fluid displaced

p can be found with mass/volume

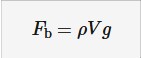
Newton’s first law

An object at rest stays at rest, and an object in motion continues in motion with the same speed and direction unless acted upon by a net external force.

equilibrium

if there is a zero resultant force acting on it, if body is at rest or moving at a constant velocity.

Newton’s second law of motion

The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass, represented as F = ma.

Linear momentum

The product of the mass and velocity of a body, greater the linear momentum the harder it is to stop.

• Linear momentum is a vector quantity, direction of linear momentum is same as direction of velocity of the body.

• Linear momentum remains constant unless the system is acted on by a resulted external force.

• Can be expressed as the sum of two perpendicular momentums, conservation of momentum applies separately in perpendicular directions

p = momentum ((kg*m)/s)

m = mass (kg)

v = velocity (m/s)

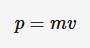
Internal vs External Systems

• Forces F₁ and F₂ act between the two skaters, which are the system. F₁ and F₂ are called internal forces.

• Weights W₁ and W₂, are exerted by the Earth on the skaters. Since the Earth is not part of the system, these forces are external.

• The ice pushes the skaters up, and since the ice is not part of the system, the normal forces are also external.

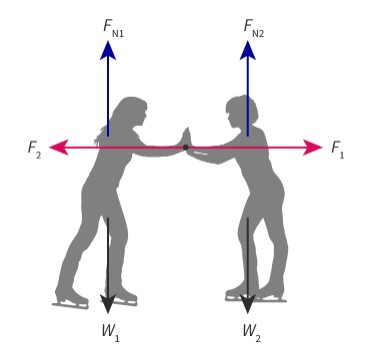
Conservation of Momentum

Momentum is conserved when the resultant external force equals zero. That means that there are no external forces, or the external forces sum to zero. We call this type of a system an isolated system. If system is isolated total momentum of the system is conserved.

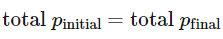
Changing Momentum

Alternate equation for determining force,

allows for mass to be changing for example airplane using fuel during flight.

Delta p = change in momentum

Delta t = change in time

F = force (newtons)

p can be replaced with mass*velocity, assuming mass stays the same we can rewrite as mass*change in velocity/ change in time. Which is mass*acceleration.

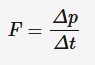
Impulse

The change in momentum of a body, usually caused by a collision or impact. The only forces that can change the total momentum of the whole system are the external forces

J = impulse (kg*m*s^-1)

F = average resultant force (newtons)

delta t = time in contact (seconds)

Period

The time taken for one complete cycle of a periodic motion, often measured in seconds. It is inversely related to frequency, which is the number of cycles per second.

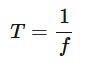
frequency

The number of cycles of a periodic motion that occur in one second, measured in hertz (Hz). It is the reciprocal of the period.

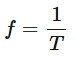
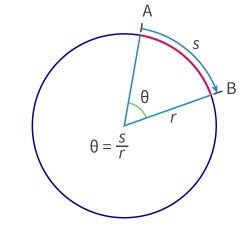
Finding Arc Length

s = theta*radius, where s is arc length

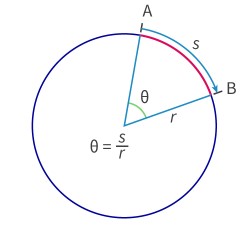
Finding theta in circle

theta = s/radius, where s is arc length

Speed in regards to circular motion

Speed of a body going in a circle is the length of the arc covered in a specific amount of time. Uniform circular motion is circular motion with a constant speed.

• v = speed (m*s^-1)

• r = radius (meters)

• T = period (seconds)

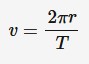
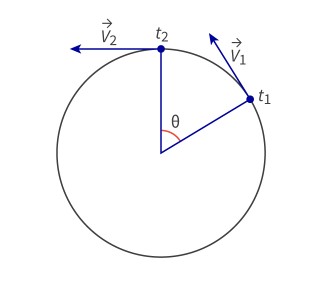
Angular Velocity

The vector quantity that describes how quickly a rotating object is rotating around its axis.

• direction of vector is always at a tangent to the circle.

• rate of change of the angle covered by the body (rads*s^-1)

• can also be determined with w = (2pi)/T

• speed = angular_velocity*radius

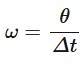
Centripetal acceleration

The acceleration experienced by a body as the body moves in circular motion. The direction of centripetal acceleration is towards the centre of the circle.

a = v^2/r , where a is centripetal acceleration (m*s^-2), v is speed (m*s^-1), r is radius (meters)

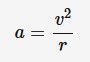
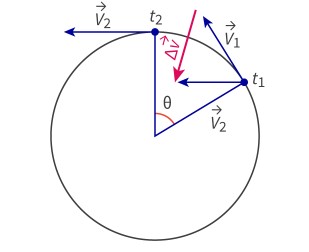
Determining change in velocity in uniform circular motion

The change in velocity vector, Δv, points towards the centre of the circle. Acceleration is the rate of change of velocity, so centripetal acceleration also points towards the centre of the circle.

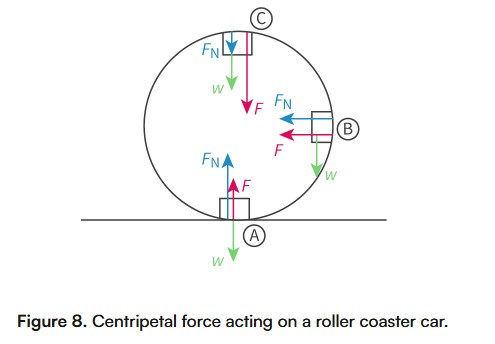
Centripetal Force

The force exerted along the radial axis on any object that moves on a circular path.

• F is centripetal force (Newtons), m is mass (kg), v is speed (m*s^-1), r is radius (metres)

• is the resultant force directed radially towards the centre of the circle that keeps the body moving in a circle

• acts perpendicular to the velocity

• causes the body to change direction and accelerate even though the speed is constant

• is always provided by another force, such as tension force, frictional force or normal force.

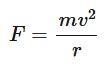
Kinetic energy

Active energy of a mass in motion, measured in joules 

• You can see that, at constant velocity, kinetic energy is proportional to mass (E⁢k∝m), so that doubling the mass means doubling the kinetic energy.

• For a constant mass, the kinetic energy is proportional to the square of the velocity (Ek∝v2), so that doubling the velocity means increasing the kinetic energy by a factor of four.  

• W = Δ⁢Ek = (1/2)⁢m⁢Δ⁢v^2

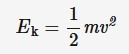
Gravitational potential energy

Energy stored by a mass due to its position within a gravitational field, measured in joules

• m = mass (kg)

• g = gravitational field strength (N*kg^-1)

• Δh = change in height (m)

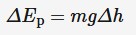
Elastic potential

Energy stored by an object that has been deformed, measured in joules.

• it is not possible to simply multiply the final displacement (extension) by the final applied force, because the applied force changes as the spring stretches.

• k = spring constant (N*m^-1)

• Δx = change in length (m)

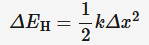
Work

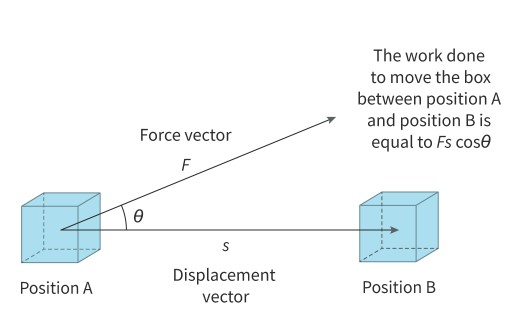
The amount of energy transferred when an external force moves an object over a displacement. Work done is the product of the displacement of an object and the component of the force acting on the object that is parallel to the object’s displacement. It is measured in joules (J). 1 joule is equal to one newton meter.

• Work is a scalar quantity

•  work done = area under the line of a force–displacement graph

principle of conservation of energy

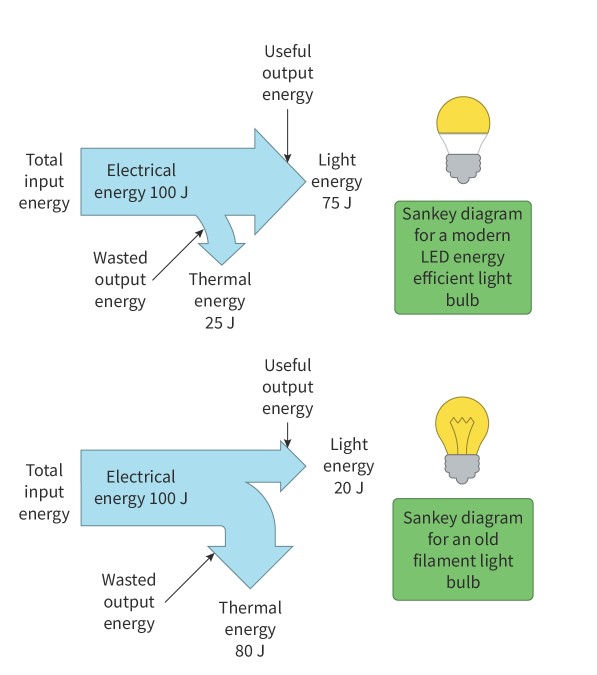
The law stating that the sum of the useful and wasted energy outputs of an isolated system is always equal to the total energy input. Energy can only be transferred, it cannot be created or destroyed.

Sankey diagram

A scale diagram used to represent the total input, the useful output and the wasted output energies within a system.

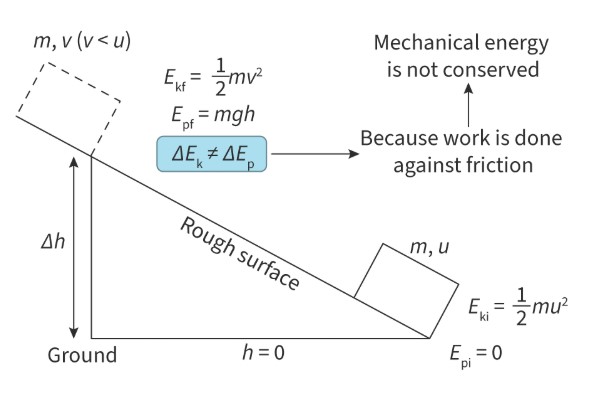
mechanical energy

In an object, the sum of the kinetic energy, gravitational potential energy and elastic potential energy.

power

The rate of work done (or the rate at which energy is transferred). It is measured in watts (W).

• ΔW = work done (J)

• Δt = time (s)

• work is equal to joules per second

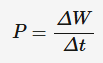
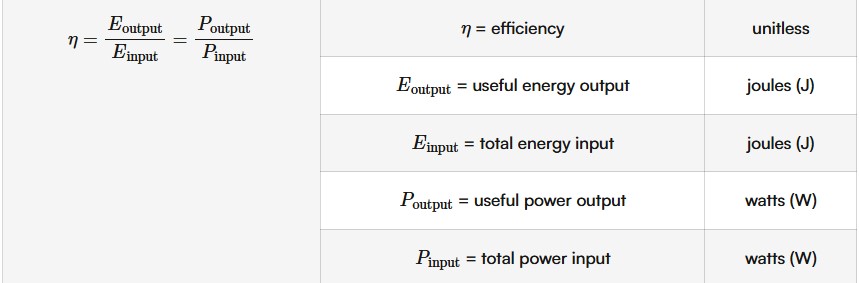
efficiency

The ratio of useful energy output to total energy input (or the ratio of useful power output to total power input).

energy density

The ratio of energy stored within a fuel to the volume of a fuel. It is measured in joules per cubic metre (J m⁻³).

fuel

A substance that can be made to react with other substances in order to transfer thermal energy or mechanical energy that can be used to do work.