2. Nash Equilibrium

What is a best response correspondence?

• A best response correspondence is the set of strategies which are best responses to another players strategy set S_-i

What role do beliefs play?

• Beliefs are the mechanism by which a person can decide what their best response actually is

• Whilst knowing what the best response to a particular strategy is, we can only guess the actual strategy which is going to be played through beliefs

How is a Nash Equilibrium (NE) defined formally?

• A strategy profile s* = (s₁*, . . . ,s_n*) is a Nash Equilibrium if, for all i ∈ N, s_i* is a best response to s_-i*, i.e. π_i(s_i*, s_-i*) ≥ π_i(s_i ,s_-i*)

• No player has a unilateral profitable deviation

• There are mutual best responses

• Beliefs about the other players strategies are correct, allowing for best response

• All dominant strategies or unique survivors of IESDS are Nash Equilibria

Calculating BR in continuous games

• In a continuous space, calculating a best response is very similar to the method used in the Cournot duopoly model; construct an expected payoff (profit) function and then differentiate to maximise

What is a mixed strategy?

• A mixed strategy occurs by randomising the probability of undertaking a strategy; we define a probability distribution over a finite set of strategies

  • In the case of infinite spaces a continuous distribution which squeezes into [0,1] is required

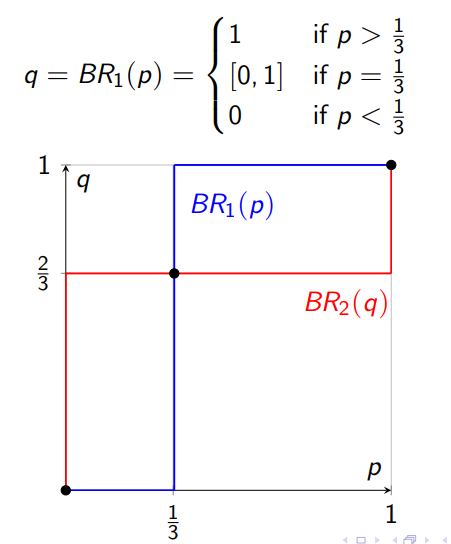
Mixed strategy normal form

• Both of these are Best Response Correspondences, where a Mixed Strategy Nash equilibria occurs where both lines cross

• BR₁(p) shows which value of q to pick for each value of p

How can NE be better than Dominance or IESDS?

• Although, in normal form, a game might not have a strictly dominant strategy or IESDS is unhelpful in reducing speculation from ‘anything can happen’, a unique NE can still be discovered by finding each players best responses in each column/row

• Strategy combinations which are best responses for both players are Nash Equilibria

Where are Nash equilibria in the Cournot and Bertand duopoly models?

• Cournot is about setting quantities; this can be calculated by deriving best response functions, and provided there aren’t too many firms, there will be a Nash equilibrium which sees firms profit

• In the Bertrand model, where prices are decided first, when prices can be any arbitrary amount (ie, less than £0.01) they are equal to marginal costs, implying competitive equilibrium

  • This can change when firms have different prices, but there is a discontinuity in the payoff function of one of the firms, and thus no NE because there can be no BR function (can’t be differentiated)

    • As prices of the more cost-efficient firm increase, there is a gap in the function where p₁ = p₂, because at this point the cheaper firm needs to split its profits; it tends towards it and is arbitrarily close, but it never actually reaches it

What are strategic complements and strategic substitutes?

• Strategic substitutes are best responses which decrease with the decision of another party; in a Cournot model, the more that player 2 produces, the lower is the best response of player 1

• This differs to strategic complements, which increase with the decision of another player; in the Bertrand model, if one party sets a higher price, the potential profits of the other party also increase, even if firms will not choose to do this and instead ‘race to the bottom’

What is the median voter theorem?

• Propose 101 citizens have different political beliefs on a spectrum from -50 — 50, one unit for every person

• A politician wins an election if they are able to run on policy which will capture the most amount of voters, situating themselves somewhere on the spectrum

  • Since a person is running against another, the BR is to situate oneself directly in the middle, meaning that the parties make themselves as similar to one another in mutual best response

• Thus, an election, theoretically, and subject to this models constraints is decided by the political opinion of the median voter

How do rationalizability and IESDS relate?

• IESDS is the process, rationalizability is the outcome

How is a mixed strategy formally defined?

• Let S_i = {s_i1, s_i2,...,s_im} be player i’s finite set of pure strategies

• Define △S_i as the simplex of S_i, which is the set of all probability distributions over S_i

• A mixed strategy for player i is an element σ_i ∈ △S_i, so that σ_i = {σ_i(s_i1), σ_i(s_i2), . . . , σ_i(s_im)) is a probability distribution over S_i, where σ_i(s_i) is the probability that player i plays s_i

• σ_i must be greater than 0, and the sum of strategies must have a probability of 1

What is a degenerate mixed strategy?

• This is just a pure strategy, which is a type of mixed strategy where one strategy has probability 1 and the others have 0, meaning it is deterministic

• A mixed strategy is simply one where more than one outcome have a non-zero chance of occurring

• A strategy is only in support of a mixed strategy if it occurs with a non-zero probability

How might we formally define a belief?

• It is a probability distribution that a person places over other people’s mixed strategies

• A belief for player i is given by a probability distribution π_i ∈ △S_−i over the strategies of his opponents

• We denote by π_i(s_−i) the probability player i assigns to his opponents playing s_−i ∈ S_−i