molecular energy storage and particle in a box

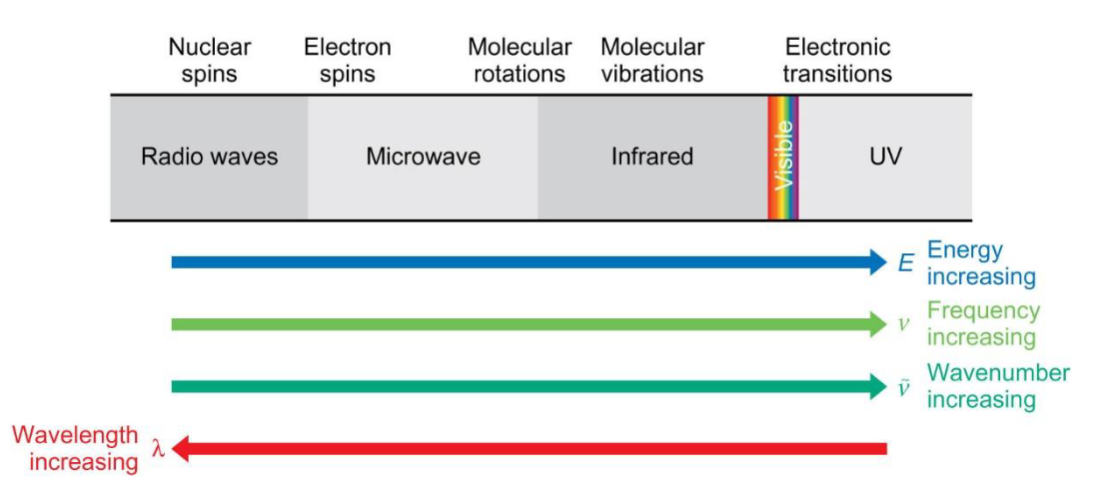
em spectrum (no x-ray or gamma) from lower to higher energy

assign: molecular vibrations, nuclear spins, electronic transitions, molecular rotations and electron spins to which region

label: increasing E, increasing frequency, increasing wavenumber and increasing wavelength

how are different forms of energy storage treated and why (give an equation)

• various forms of energy in a molecule can be treated differently

• this is because they occur on different time scales

• these energies are quantised and most (except translational) can be measured by spectroscopy

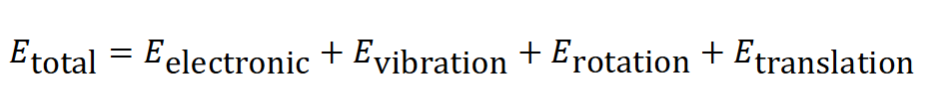
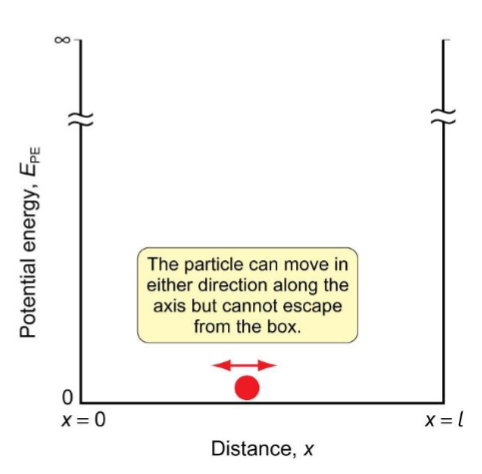
x and V for a particle confined to a 1D box of length l

diagram - “y” axis, “x” axis, movement of particle

inside: 0 ≤ x ≤ l and V(x) = 0

outside: x ≤ 0 or x ≥ l. V(x) = ∞ → the particle cannot exist in these regions of space where ψ (x) = 0

from previous set: what is the solution (for wavefunction) to the schrodinger equation in regions of constant potential?

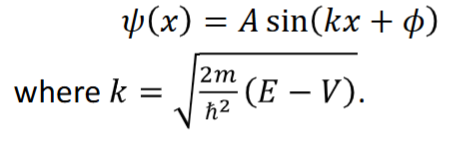
boundary conditions for particle in a box and why these are defined

what does this mean for allowed energies

as ψ (x) = 0 outside the box, and for continuity of the wavefunction, the boundary conditions are defined:

ψ (x) = 0, x = 0, l at the edges

therefore the allowed energies are integer numbers of half wavelengths of the sine wave

1st part of particle in a box derivation using the boundary conditions

at x = 0, ψ = 0. A = 0 is not an allowed condition so sin(kx+ϕ) = 0

x = 0, so Asin(ϕ) = 0

this is satisfied by ϕ = nπ

at x = l, ψ = 0.

Asin(kl) = 0 → sin(kl) = 0 → kl = nπ → k = nπ/l

ψ (x) = Asin((nπ/l)x) when 0 ≤ x ≤ l

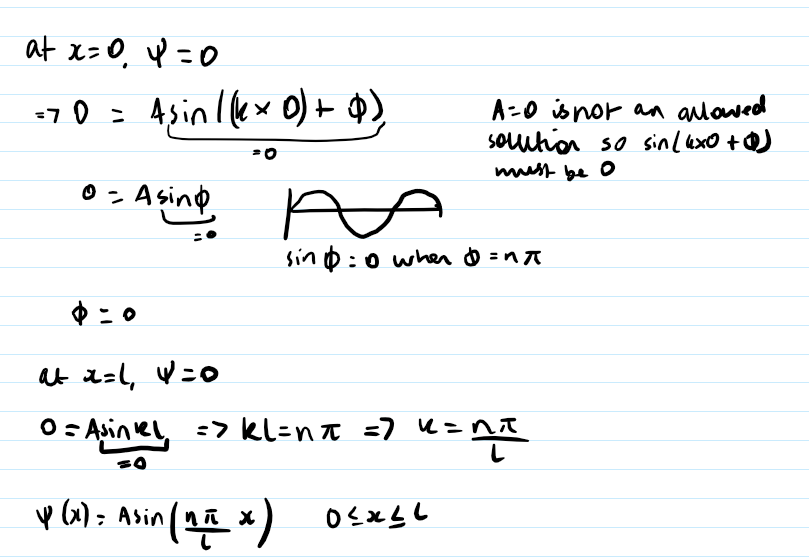
equation for E_n and how is it derived from particle in a box

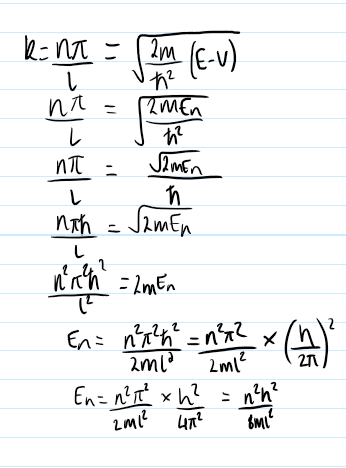
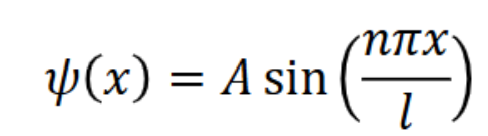
how is A found and how can the equation for ψ be expressed as a result?

1. know particle is in box so set probability to 1.

2. substitute in the equation for ψ

3. use the identity for sin²(ax)

4. solve to find A

5. put A back into equation for ψ

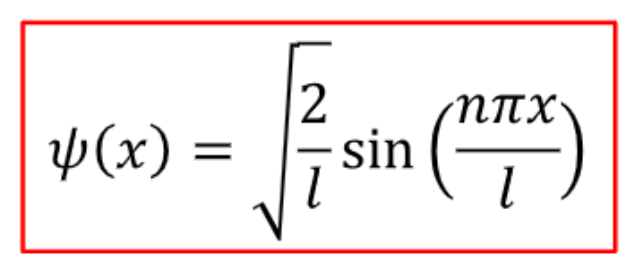
full derivation (only do after know other flashcards)

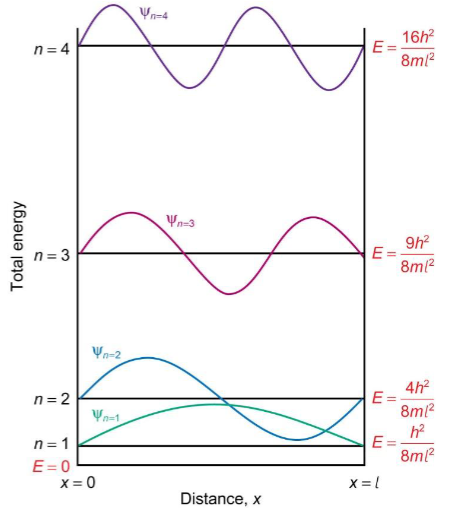
n = 1 to n = 4 particle in a box diagram including equations for E

how can the equation for E_n be derived from the de Broglie wavelength

1. inside the box, the potential energy, V, is zero, so energy is all kinetic

2. substitute v from kinetic energy into de Broglie equation

3. use the allowed wavefunctions formulae and sub in wavelength

4. rearrange to get equation for E_n - agrees with Schrodinger approach

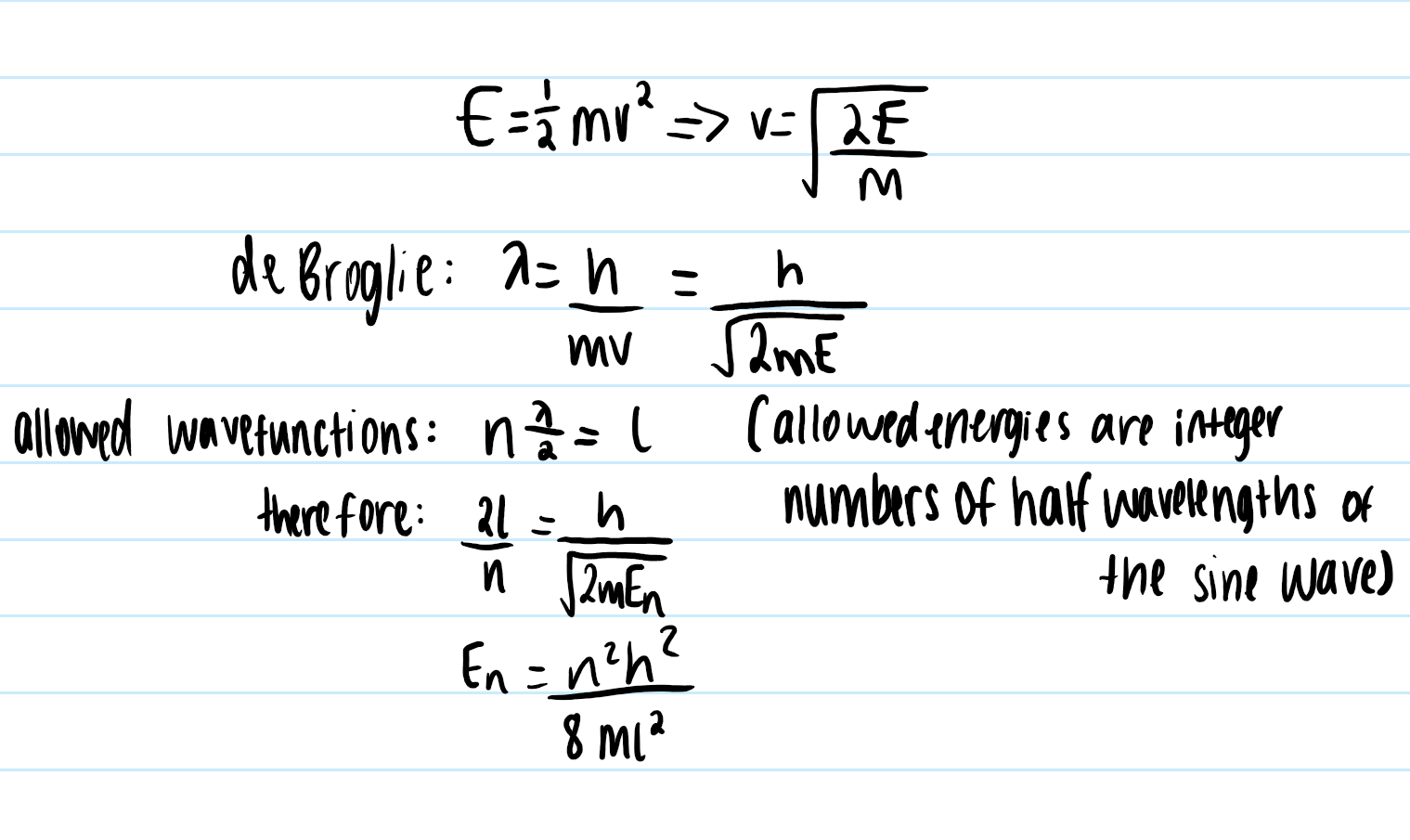
E_translation for 3D particle in a box

3D box with sides l_x, l_y and l_z

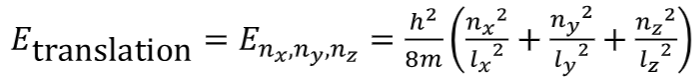
lowest energy transition and approximate ΔE for He atom in a cubic box of side 1m

comment on value of ΔE and what this means

lowest energy transition is from E_1,1,1 → E_2,1,1 (= E_1,2,1 = E_1,1,2)

ΔE ≈ 2.48 × 10^-41 J/molecule - so tiny and so transitions between translational energy levels are too small to measure, meaning translational motion can be treated as a classical continuum

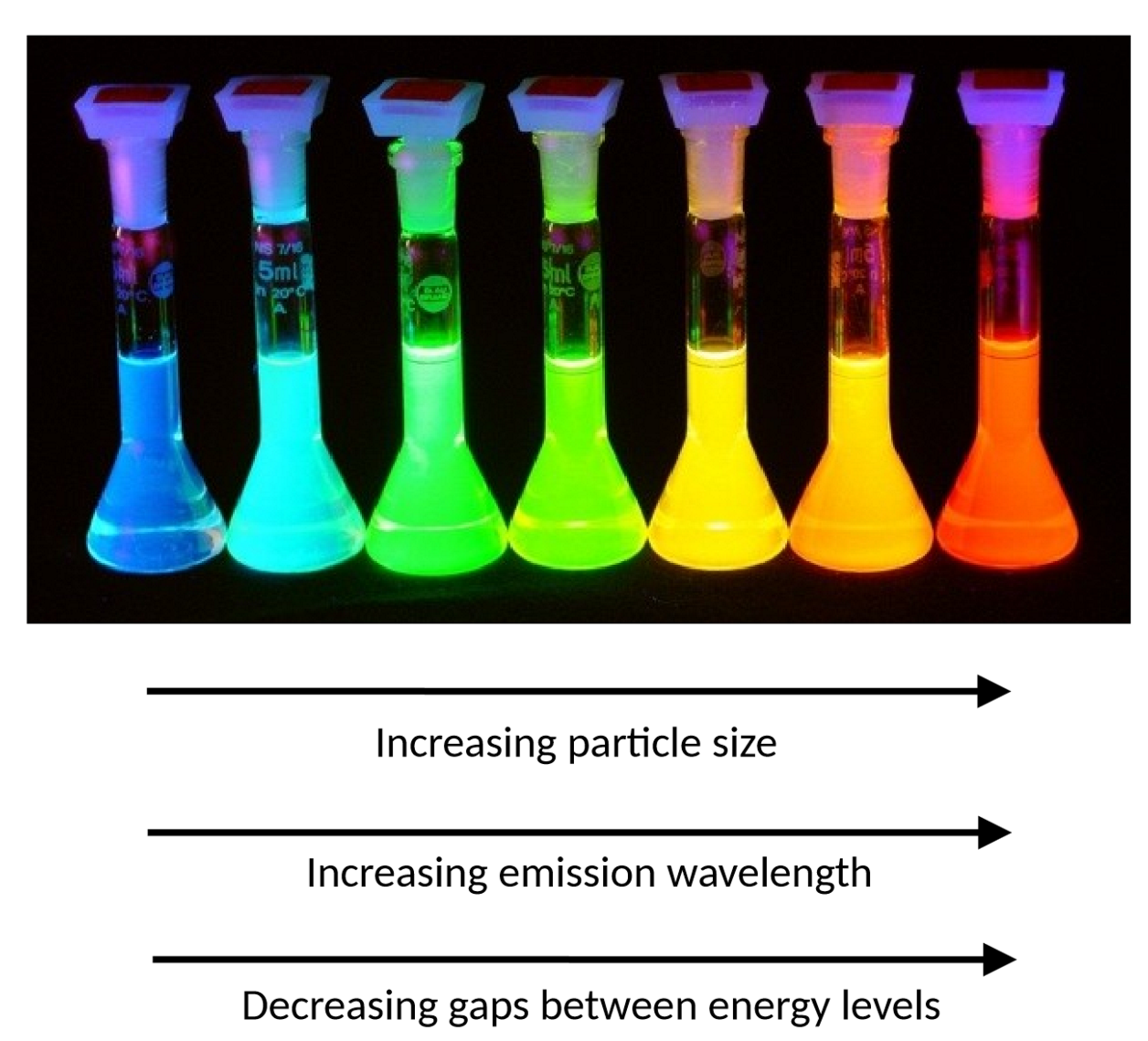
what are quantum dots

semiconducting, fluorescent nanoparticles ranging from ~2-10 nm in diameter. they emit visible light. electrons are confined to the particle so energy levels can be modelled using 3D particle in a box

emission wavelength, ΔE and particle size from left to right