AP Physics 1 Equations and Facts

Constant acceleration

• Special case freefall

• Freely falling objects experience a constant downward acceleration of 9.8 near the Earth’s surface

• Falling objects are experienced freefall when the only force acting upon them is gravity

• Free fall is a good approximation for dense objects that do not fall too fast

• Objects can be in free fall both while rising and falling

• Freely falling objects release together fall together

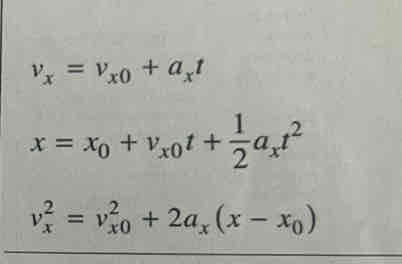
The chart

slope, equation, area

Newton’s 1st Law

• An object will not accelerate unless pushed or pulled

• Inertia=mass

• Increasing inertia decreases acceleration

• Inertia cannot prevent motion, only forces can do that

Newton’s Third Law

• For every action there is an equal and opposite reaction, always true

• No time delay between action and reaction

• Equal and opposite forces act upon different objects

Fg=mg

• Mass stays the same

• g = Freefall acceleration (can be used with constant acceleration equations for objects and freefall)

• Force of gravity = weight

a = F_net/m

• What is it touching, are you on planet, is there friction?

• Increasing inertia decreases acceleration

F_f= μF_n

• Kinetic friction: Opposes sliding created by surface bonds constantly breaking and reforming

• Static friction: Opposes motion (traction) created when surface bonds stretch without breaking

• Friction is proportional into normal force

• Independent of surface area

• Independent of velocity

• Because bonds stretch (<) and break at max (=)

• Kinetic friction is less than static friction

F_f= μkF_n

• Opposes sliding

• Bonds break and reform

• Smooth, dry, clean surfaces

• Can push an object forward if both forces are in motion

• Must break gravity into components to find normal force on a ramp

F_f= μsF_n

• Prevents sliding

• Bonds stretch (<) until they reach breaking point (=)

• Smooth, dry, clean surfaces

• Provides the force that both speeds up and slows down cars

• Must break gravity into components to find normal force on a ramp

• Static friction adjusts to match pull

J=F_net∆t

J=∆P

• Useful for sharp impact and other non-constant force problems

• P=mv

• F∆t= F vs t area

• Do not forget gravity for vertical problems

• F_net∆t=∆P=0 (momentum conserved) for isolated systems (no outside net force), sharp collisions

P_i=P_f

• Momentum conservation

• Only useful if you can track where the momentum goes

• Works well for isolated objects (F_net=0) on the system

• Good approximation for relating the velocities right before to the velocities right after a sharp collision

• m₁v_1i+m₂v_2i=m₁v_1f+m₂v_2f

• For 2D, use vector components

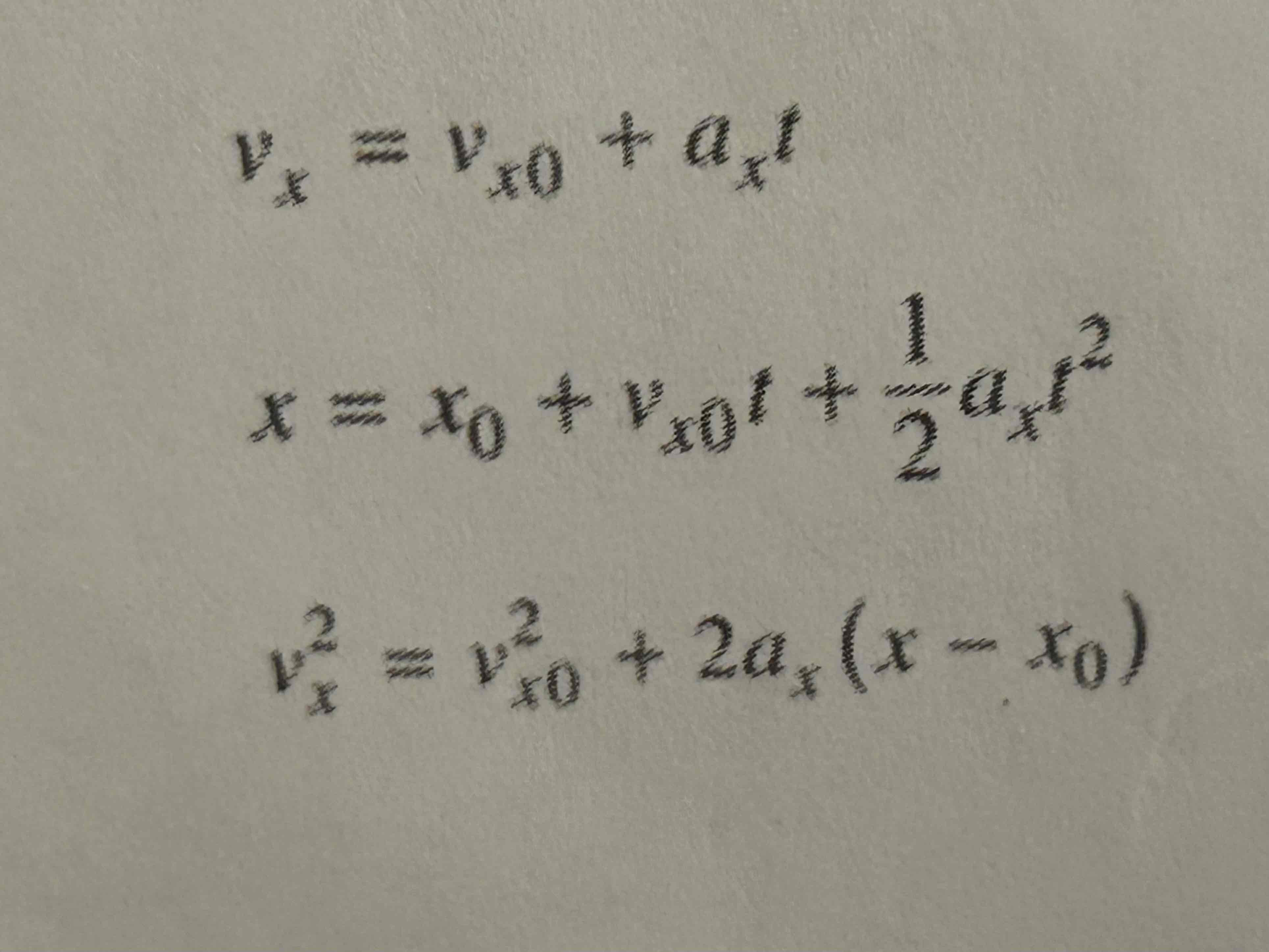
Projectile Motion

• Free fall

• Horizontal motion (x-range)

• Vertical motion (y-height)

• Velocity must be broken into x and y components

• V_oxcosθ

• V_oysinθ

a_c= v²/r

• inward acceleration due to changing direction while moving in a circle

• use inward - outward when applying fnet=ma to this situation

• single object

a=rα

v=rω

• connects system variables to single particle variables

• describes a tangential acceleration

• all points rotate the same (ω, α, θ)

• s=rθ

• 1 rev= 2π rad = 360°

θ=θ₀+ω₀t+1/2αt²

ω=ω₀+αt

• constant acceleration equations for rotational motion

• variables describe the rotational motion for the whole system

α=τ_net/I

• rotational motion version of F_net=ma

• moment-of-inertia increases as mass moves farther away from the fulcrum

L=Iω

• angular momentum definition

• L_i=L_f angular momentum conservation

• Always true, but only useful for isolated systems and sharp collisons

• L=mvr_perp for colliding objects

ΔL=τΔt

• Angular version of F_net=ΔP

• Useful for sharp impact and other non-constant force problems

• τΔt= τ vs t area

W=Fᵢᵢd=Fdcosθ

Pₐᵥ₉= W/△t=△E/△t

Pᵢₙₛₜ=Fᵢᵢv=Fvcosθ

• Work describes the transfer of energy

• Net work equals the change in kinetic energy

• Area under the F versus D graph equals work

• Power describes how fast work is done

△Ug= mg△y

UG=-Gm₁m₂/r

• GPE ?: is it off the ground?

• mgh: it’s a formula that works well near a planet’s surface

• Second formula needs to be used away from the surface

• Earth/object system must be used

Fs=-k△x

△Us=1/2k(△x)²

• SPE ?: is there a compressed or stretched spring?

• Hooke’s Law: Spring force is proportional to stretch

• Object/spring system must be used

K=1/2mv²

K=1/2Iω²

• KE ?: Is it moving?

• KEᵣₒₜ ?: Is it spinning?

• v=rω if the object rolls without slipping

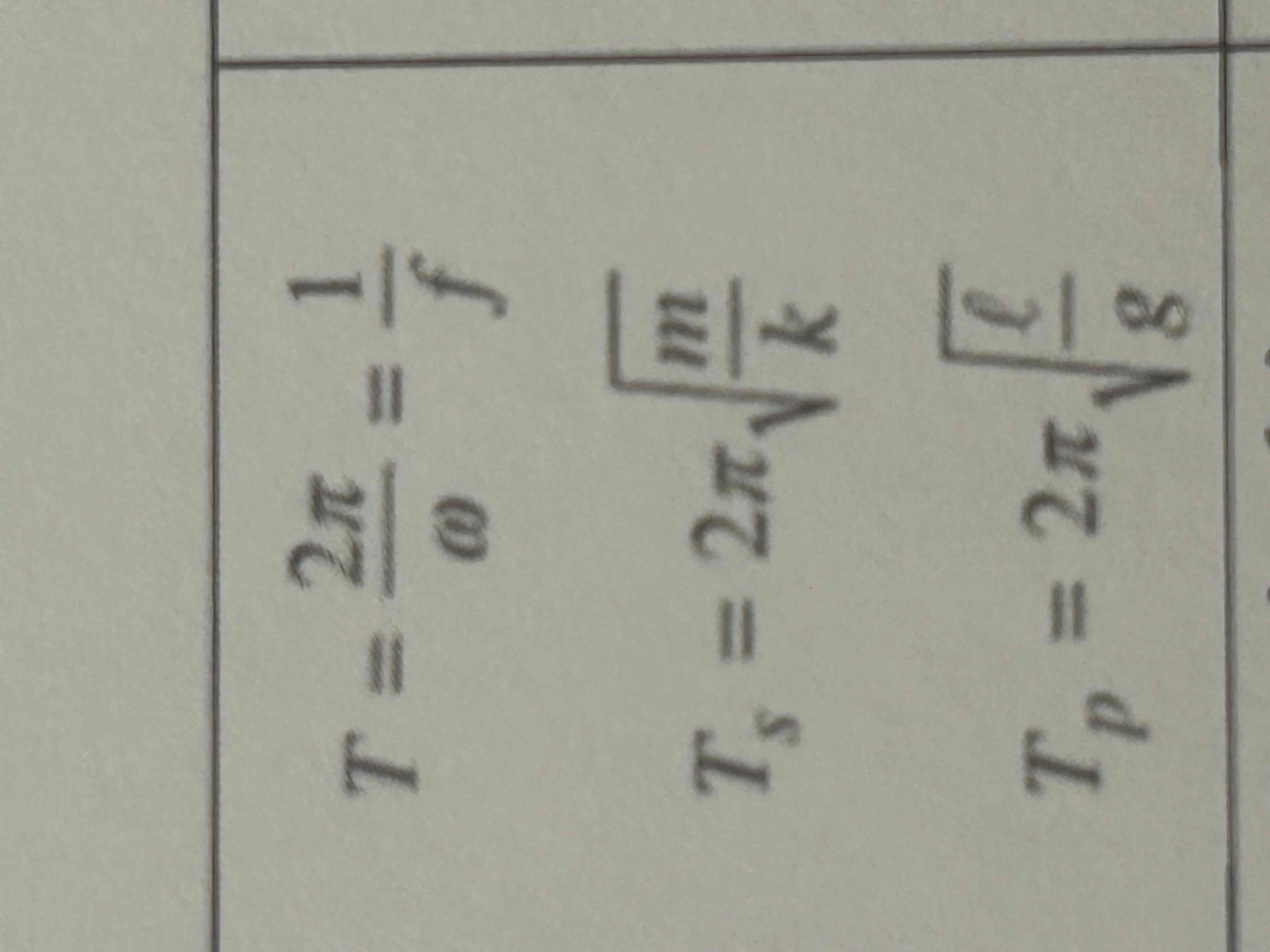
• Period is independent of amplitude for both a pendulum and a spring-made system

• Pendulum period is independent of mass, too

• Equation describing an oscillating mass-spring system (Simple Harmonic Oscillator)

• x vs t graph is a sinusoidal with the amplitude telling you the max displacement from equilibrium