L3: Structural loads and internal responses P2

Infinitesimal

Very very small

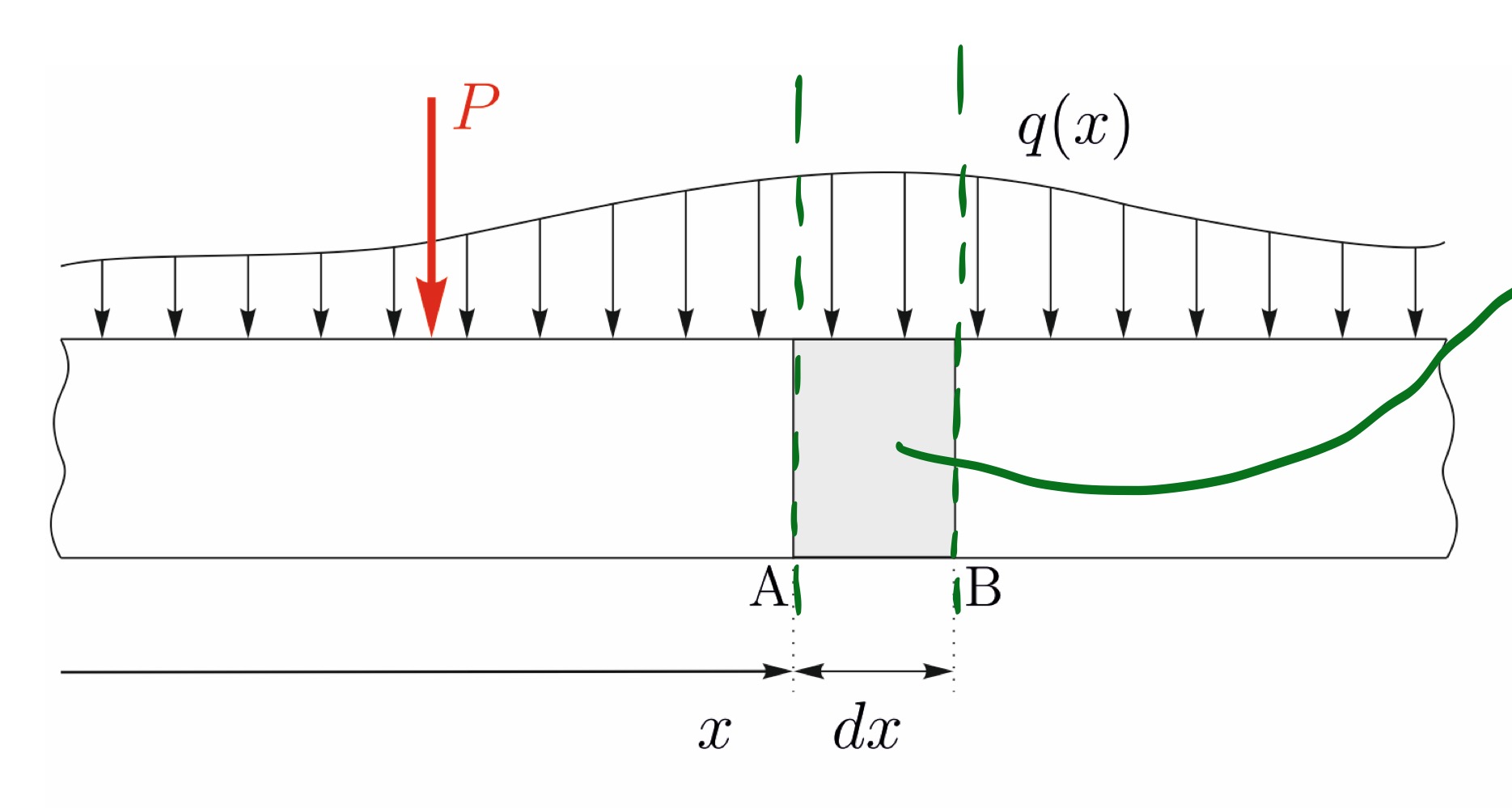
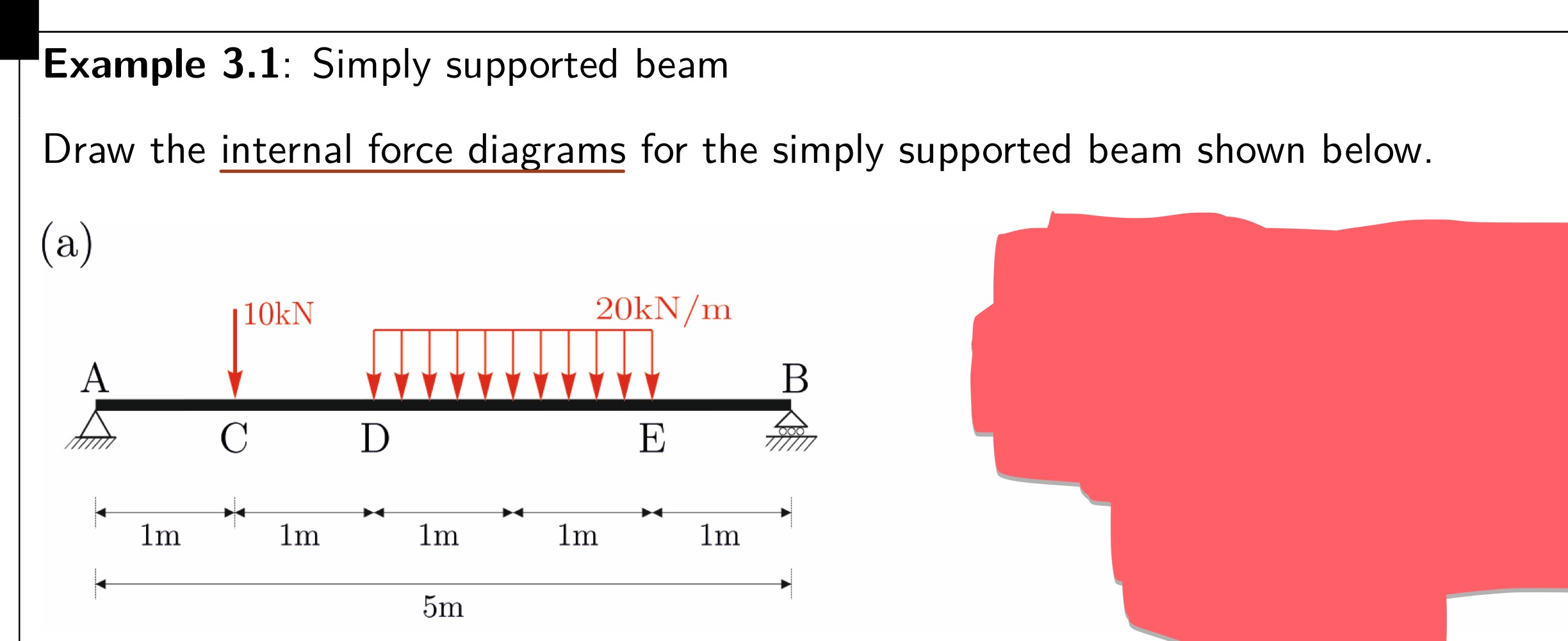
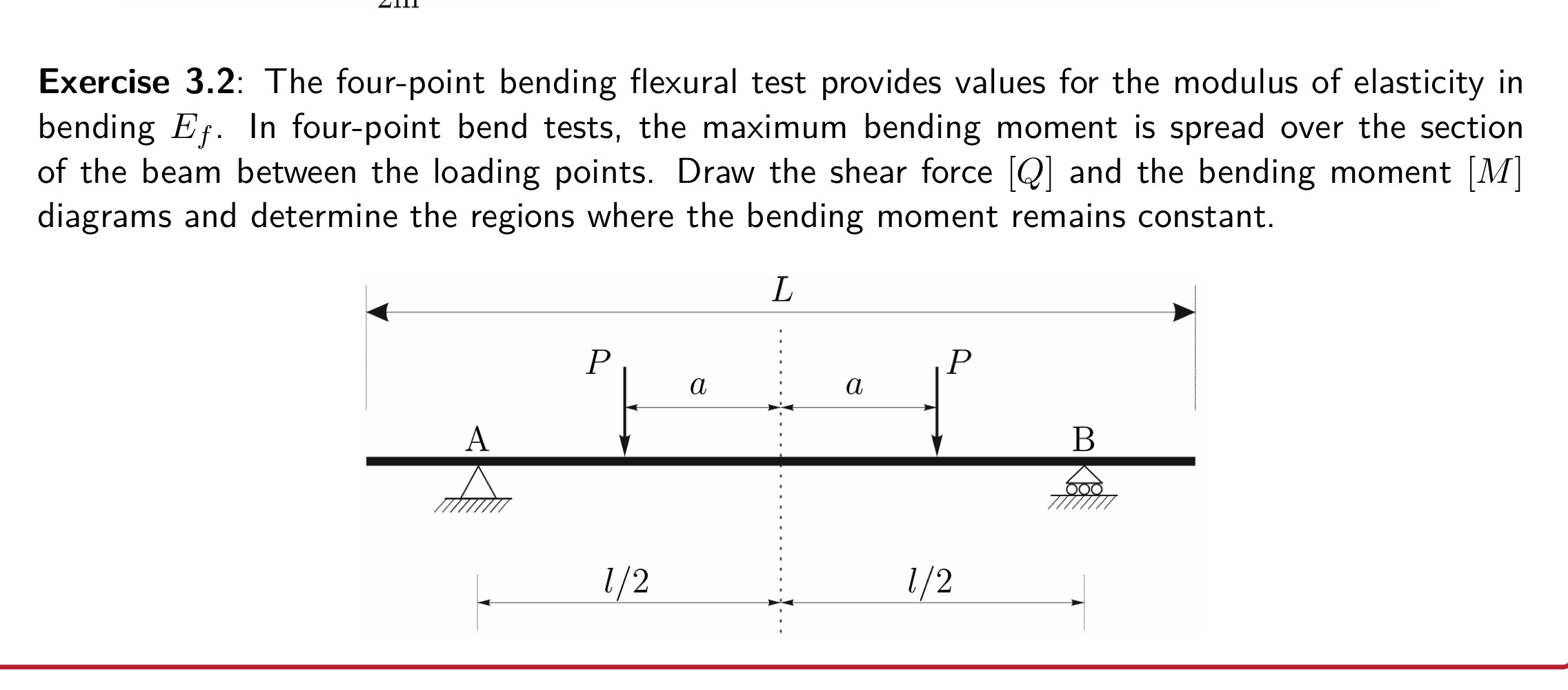
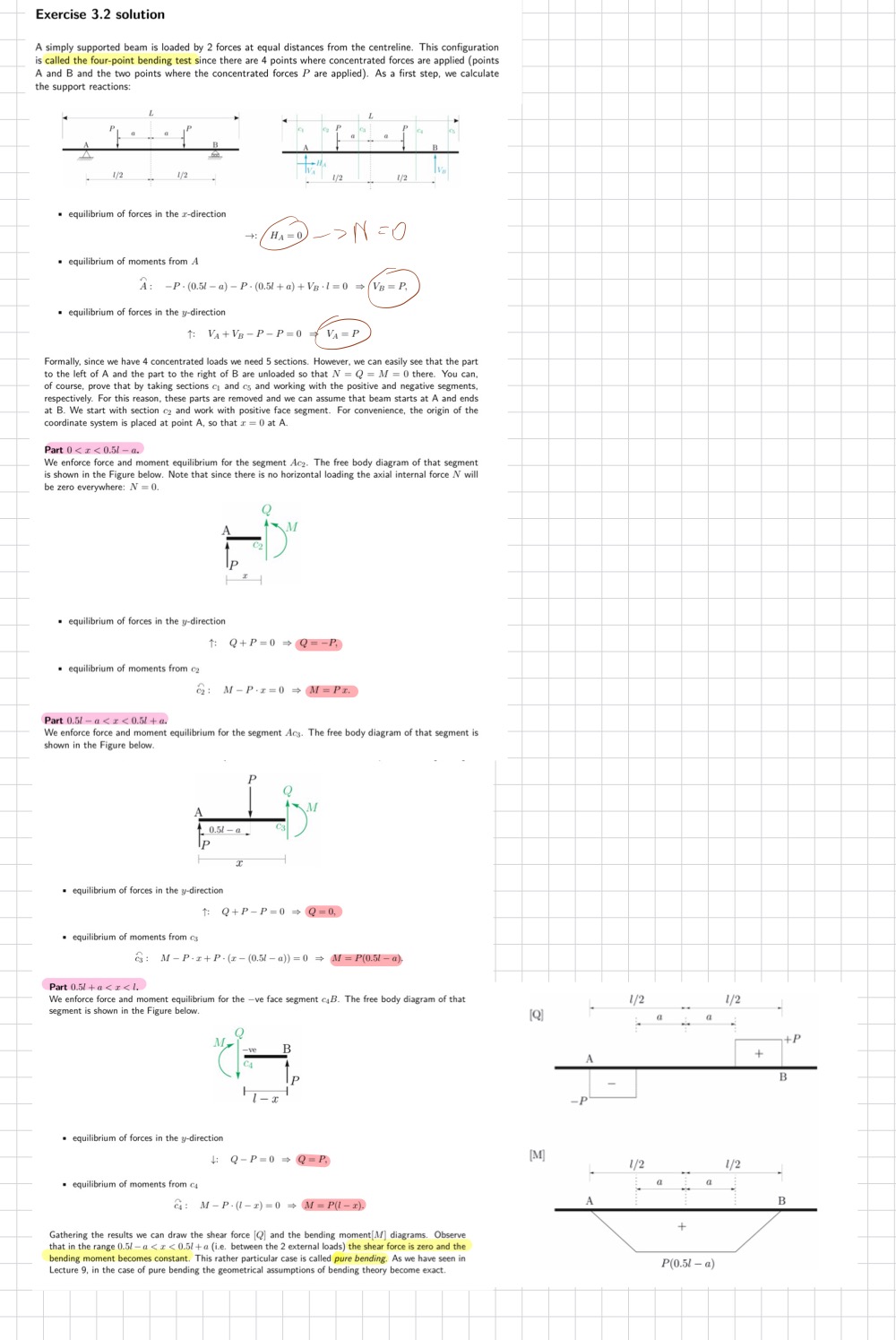
Show equilibrium of an infinitesimal element dx of the beam

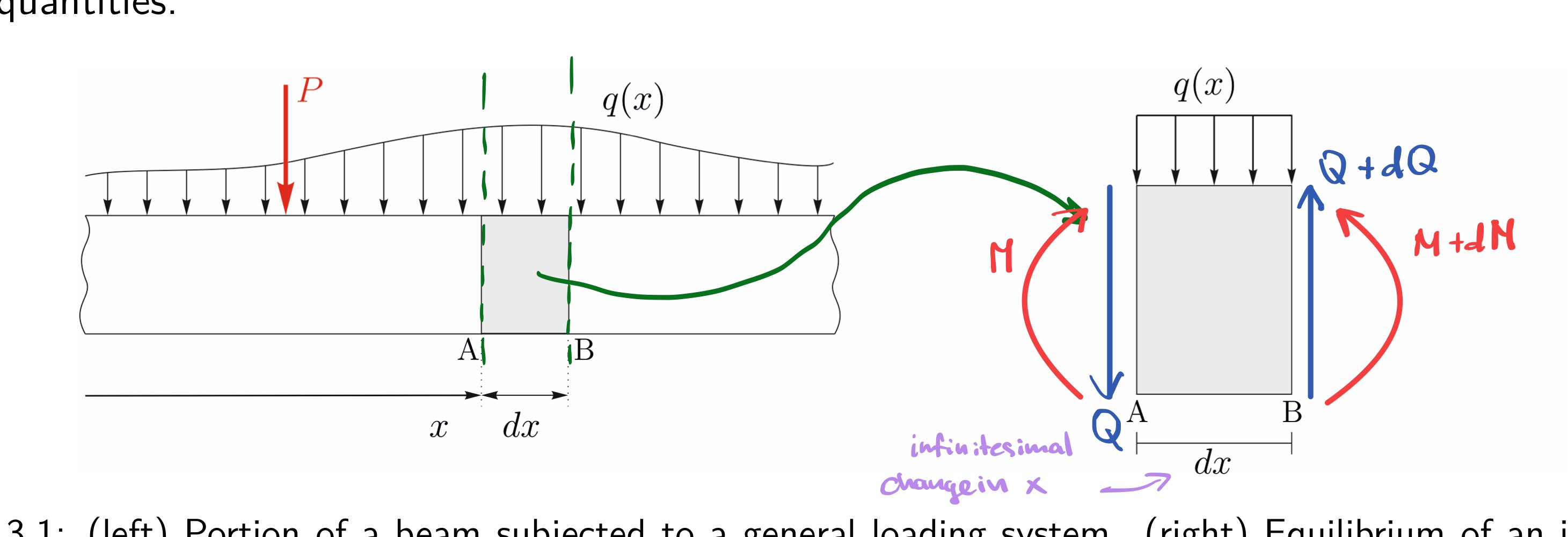
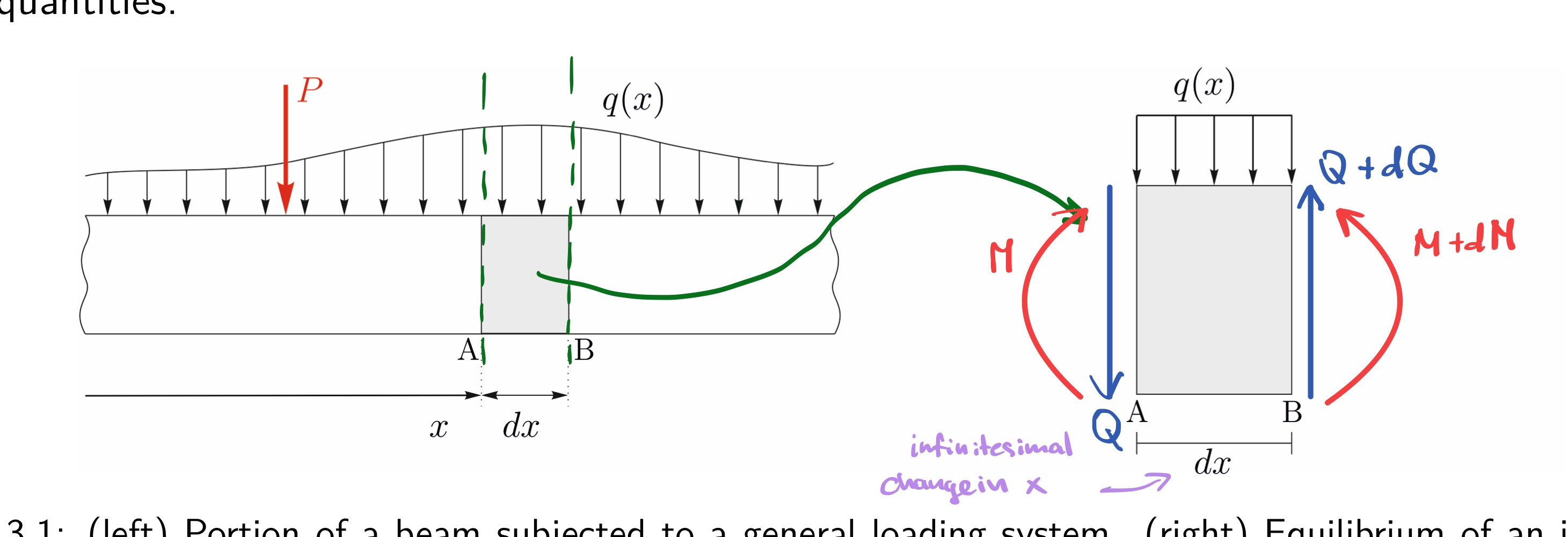
From this section of a beam, what equations can be derived

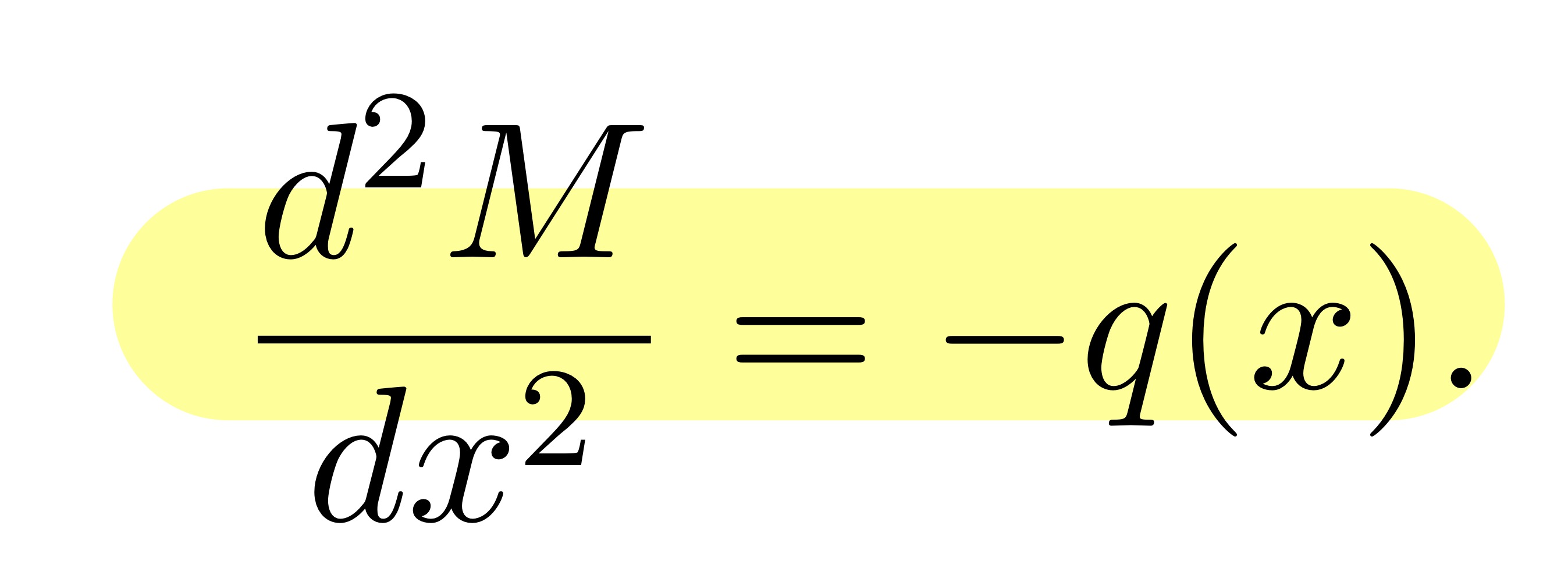
How do you exactly derive this equation?

Q and M are….

Not mathematically independent

Q tells us…

Q tells us how fast M is changing as we move along the beam

M is…

A curve

Why Q=0 when M is max?

When M is maximum, it’s like the max point on curve so no slope so differentiation is 0. So when M is max, Q is 0. When M increases, Q is positive. When M decreases, Q is negative. When M is max or min, Q is 0.

Why do we care that Q=0 when M is max?

M max usually causes highest stress and failure risk. So we set Q=0 and calculate max M. BUT! Q=0 gives local maxima/minima, not always the biggest value.

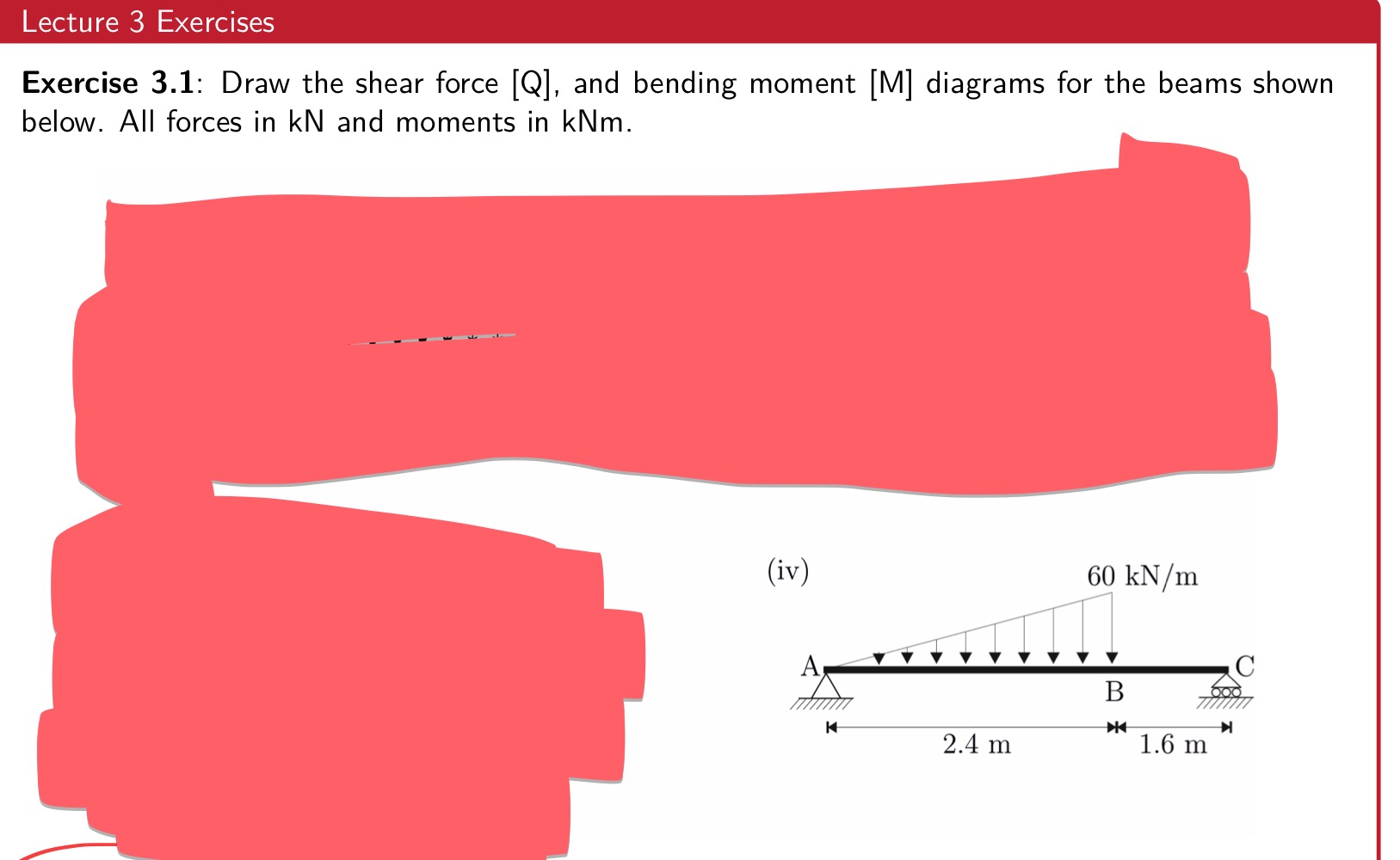
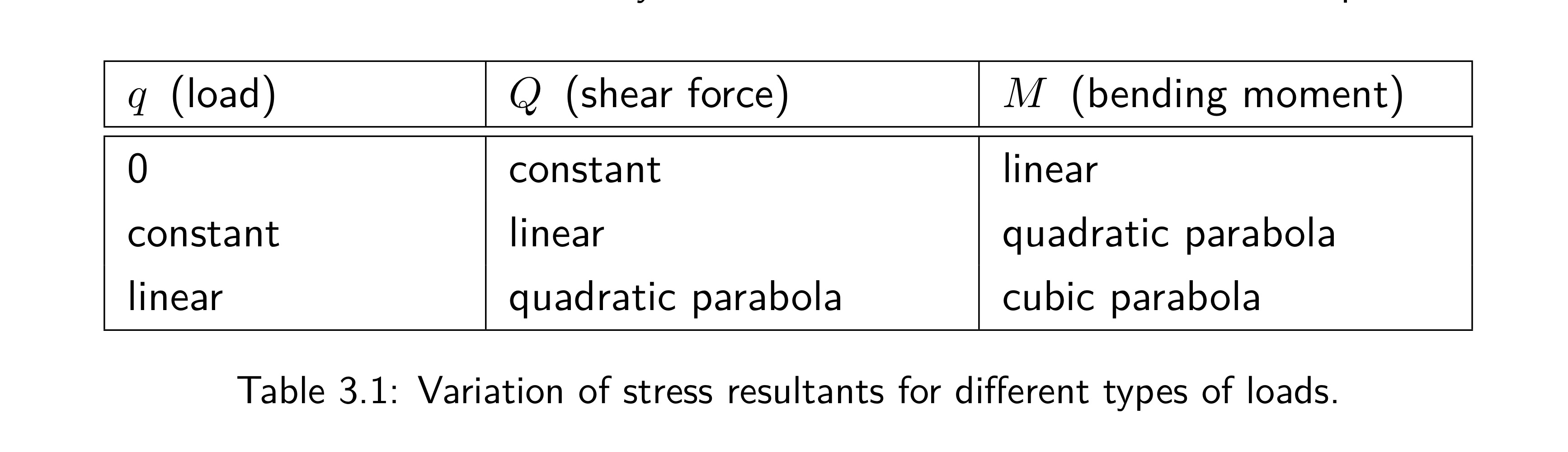
If q(x) is a Uniformly Distributed Load (UDL) of intensity q0, i.e., it is not a function of x, then equations show (by integrating) that the shear force Q will be …, while the bending moment M will be …

If q(x) is a Uniformly Distributed Load (UDL) of intensity q0, i.e., it is not a function of x, then Eqs (3.4) and (3.6) show (by integrating) that the shear force Q will be a linear function of x, while the bending moment M will be quadratic function of x.

If q(x) = 0, then the shear force is …, while the bending moment is …

If, on the other hand, q(x) = 0, then the shear force is constant, while the bending moment is a linear function of x

special case exists when the shear force Q is zero and the bending moment M is …. This situation is called …

special case exists when the shear force Q is zero and the bending moment M is constant. This situation is called pure bending

Equation of shear force Q in case of a concentrated force P

Equation of moment M in case of a concentrated moment M0

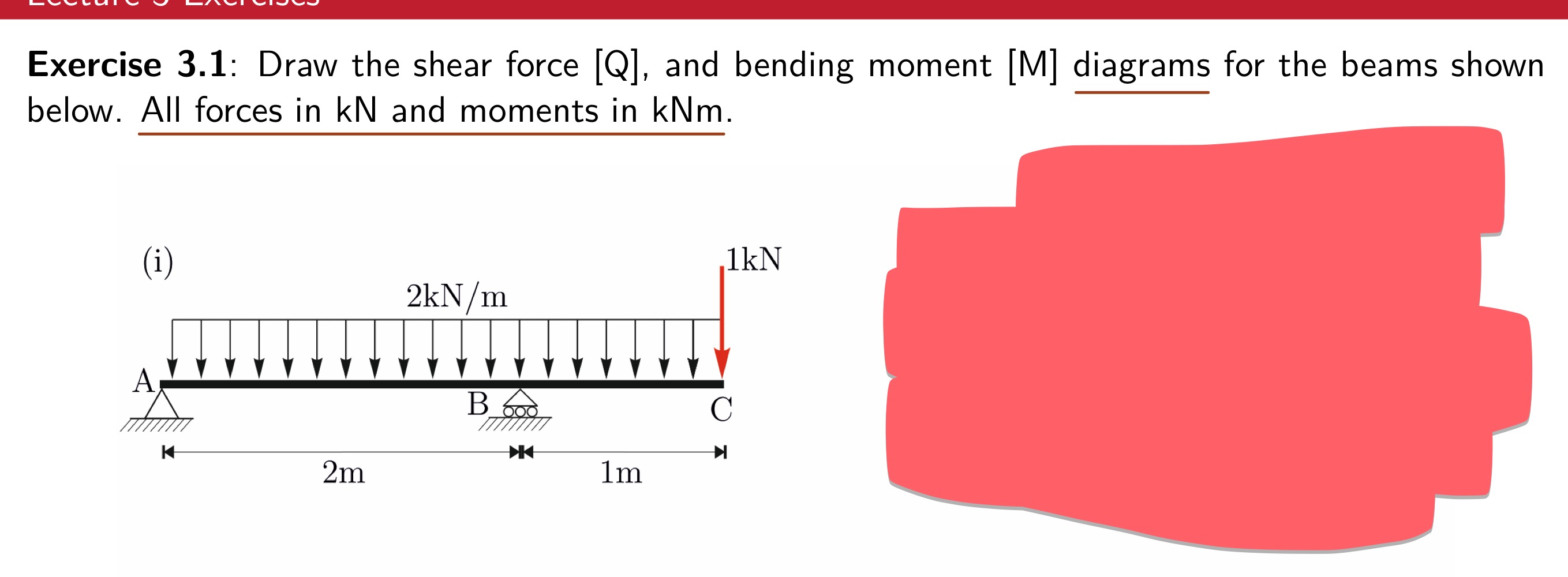
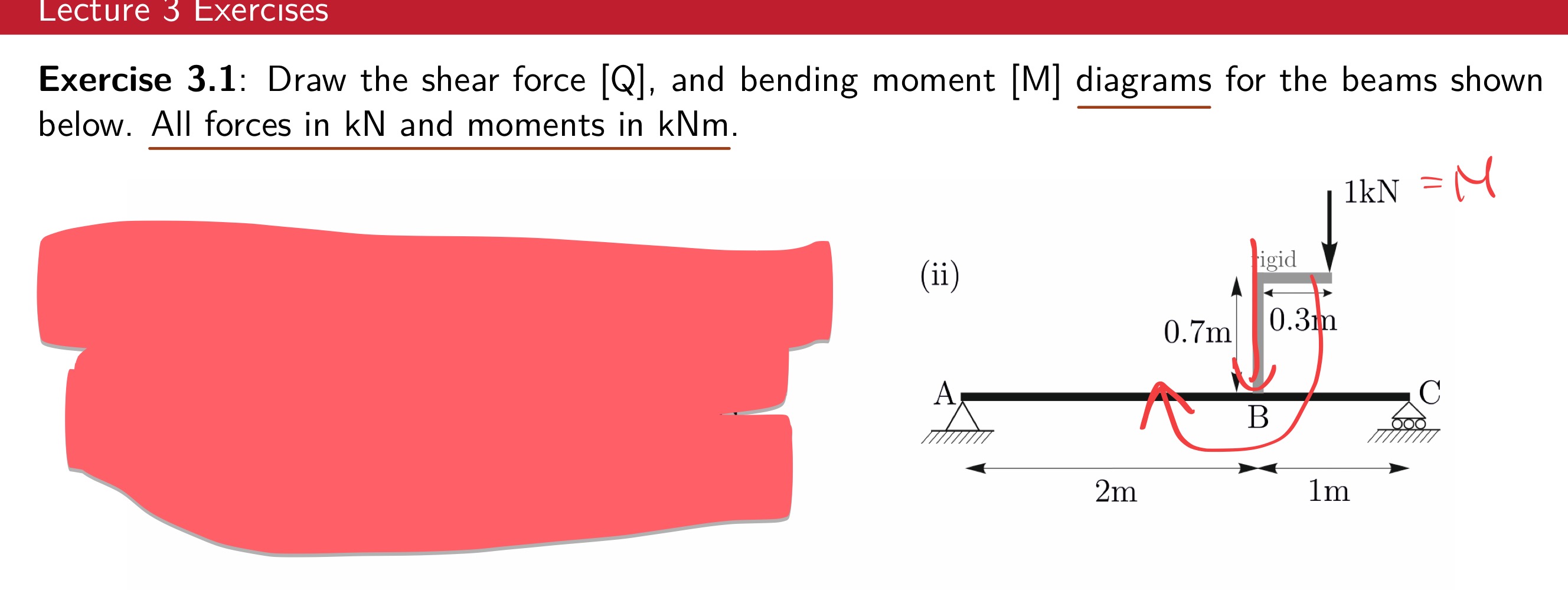
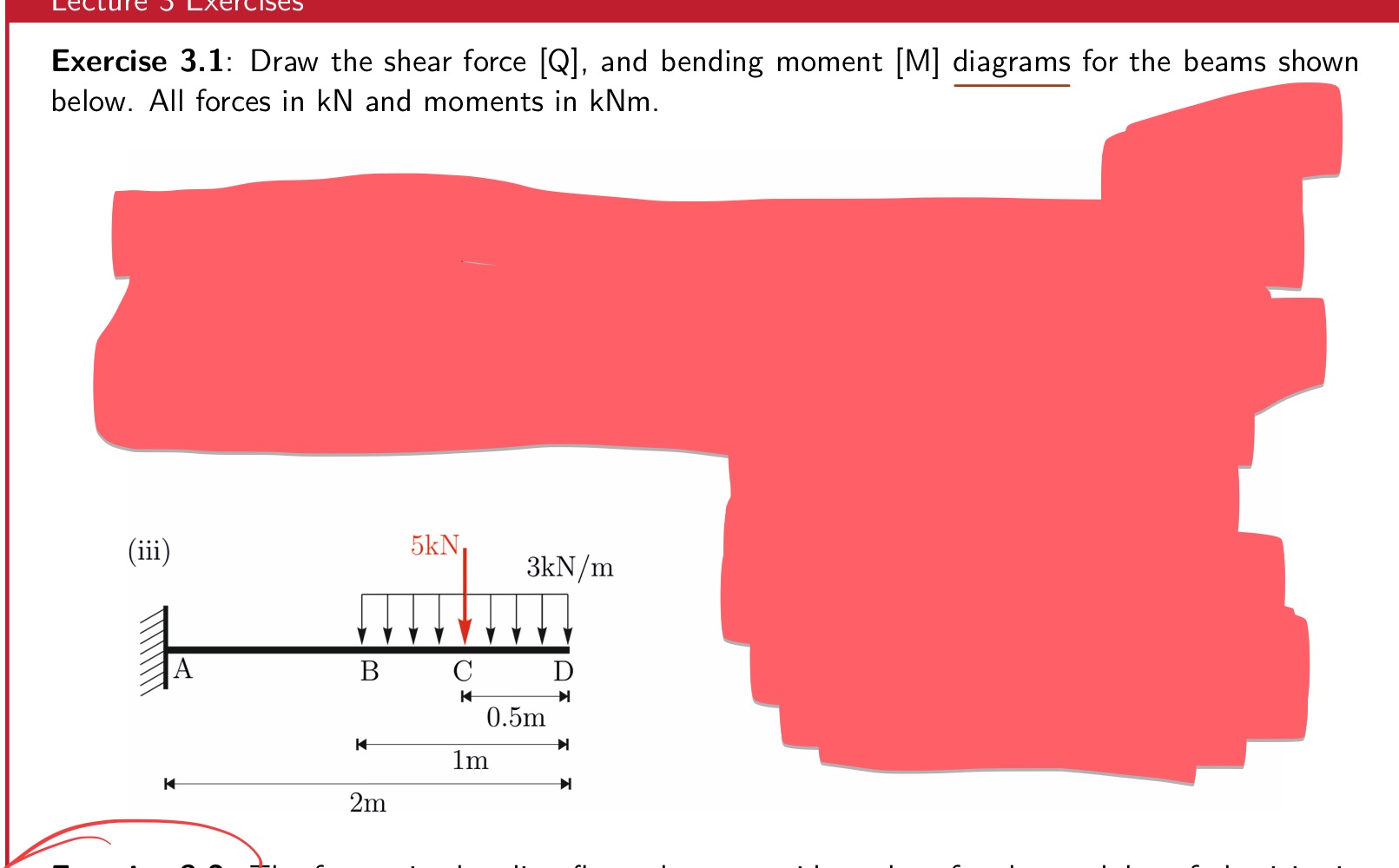
Variation of stress resultants for different types of loads

Behaviour of stress resultants at the point of load discontinuities

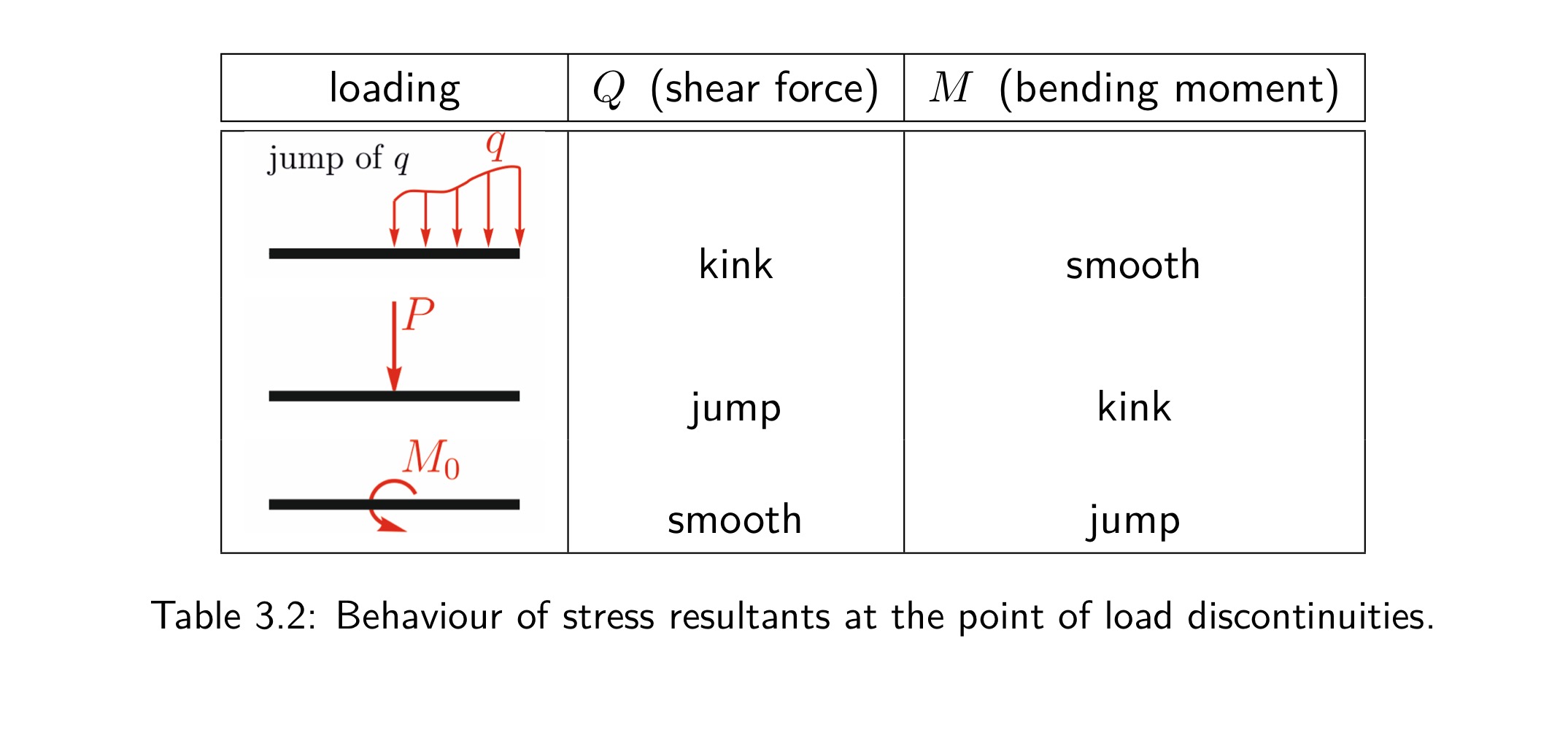
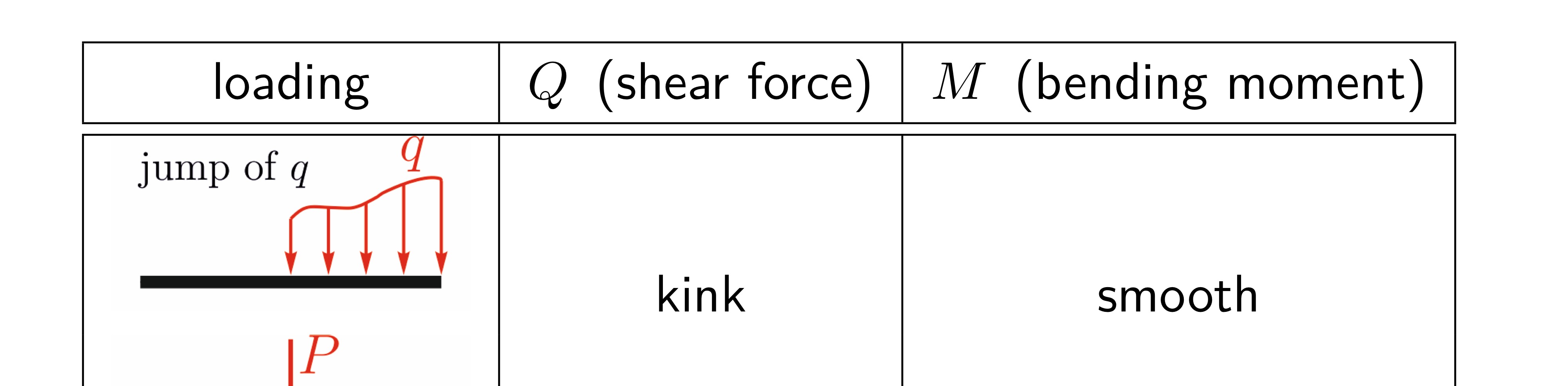
Explain mathematically

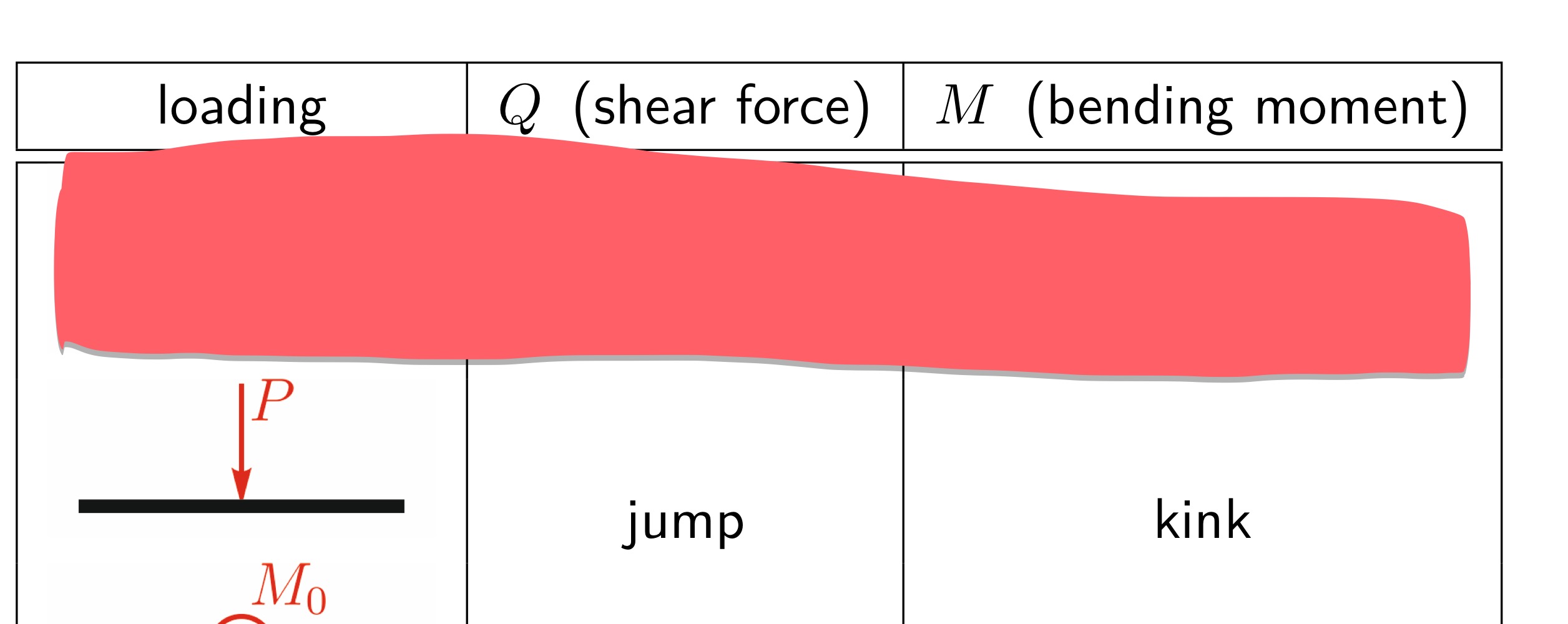
Explain mathematically

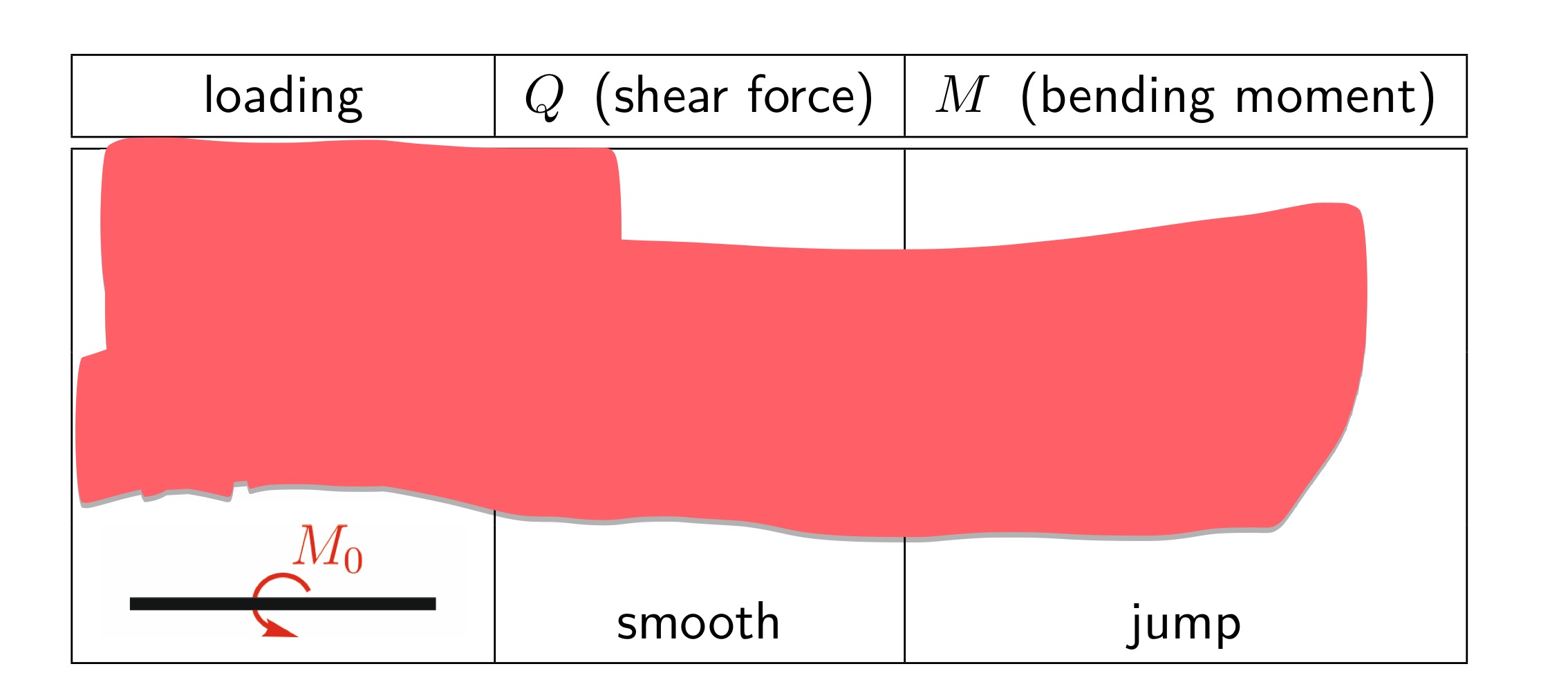
Explain mathematically