Unit 5 - random variables

Random variable

A numerical value whose value depends on the outcome of a chance experiment

Discrete vs. continuous random variable

• Discrete: the variable is a set of possible integer values

  • ex: the number of cats = {0, 1, 2, 3}

• Continuous: A set of possible values that includes an entire interval (within a certain range)

  • ex: how long it takes to bake = 0 ≤ X ≤ 100

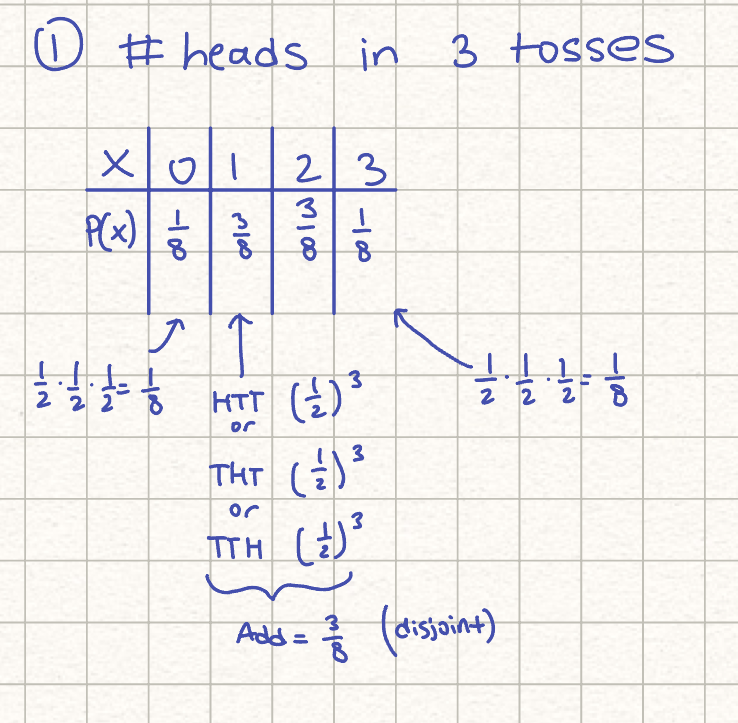
Probability distribution of random variable

Add to 1

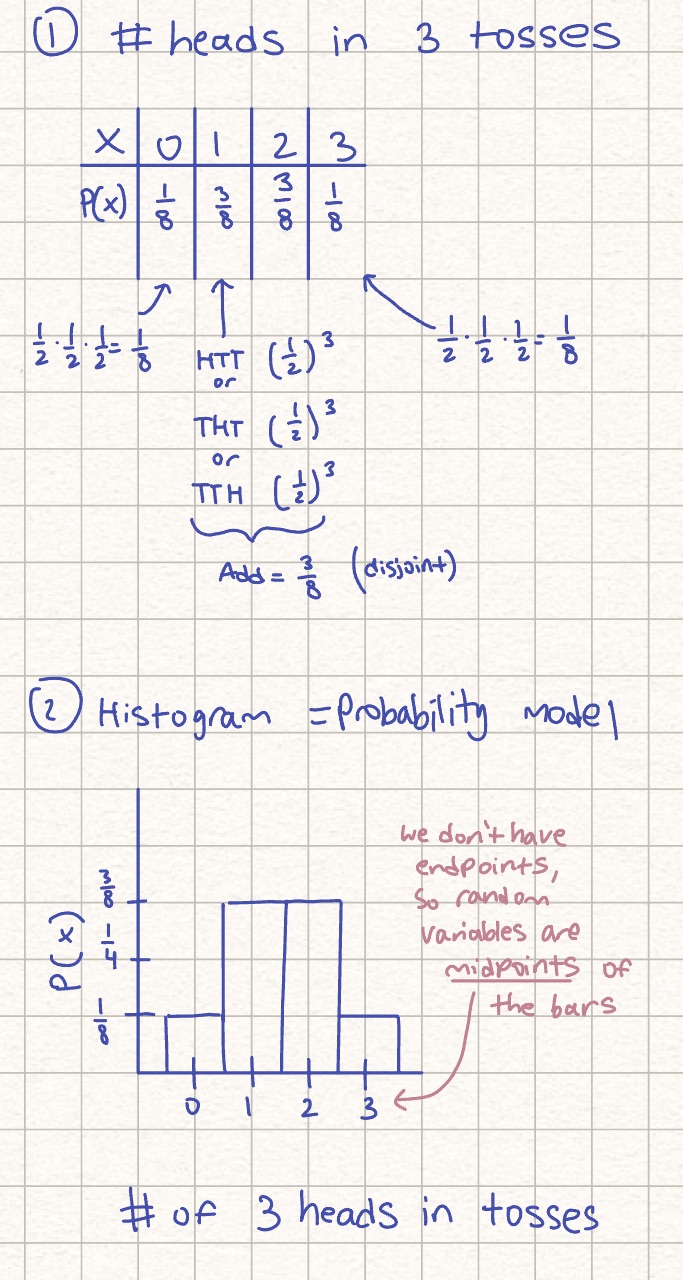
Probability histogram

P(1 ≤ X ≤ 3) ≠ P(1 < X < 3)

Expected value of random variable [by hand]

• Expected value = mean

Standard deviation of random variable [by hand]

Mean & SD of random variable [calculator]

• Go to list

• Enter random variables in L₁

• Enter probabilities in L₂

• Stat → 1vars

• Set list: L₁

• FreqList: L₂

What happens to mean/SD/variance when adding/subtracting?

Measures of position change, measures of spread do not

What happens to mean/SD/variance when multiplying/dividing?

Both measures of position and spread change

Adding or subtracting random variables

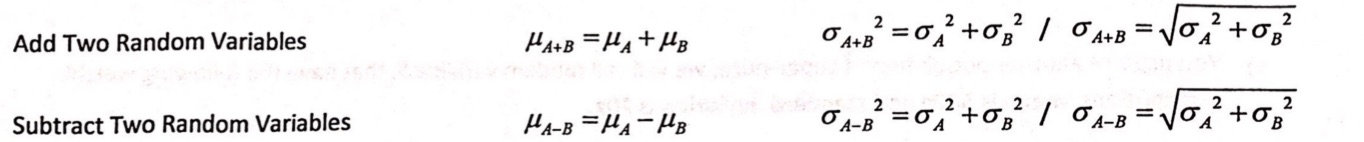
Adding random variables, one of them is multiplied by a constant

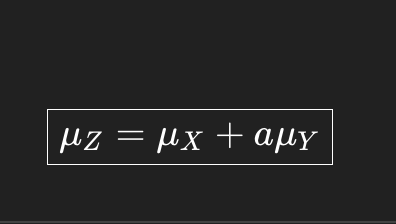
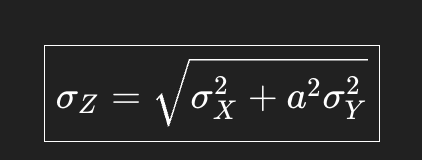
How to normal distribution combining variables

• Combine mean and standard deviation

• Make a new graph with new mean and standard deviation

Conditions for a binomial setting

• Binary = either a success or failure

• Independent

• Number = the number of trials n of the chance process must be fixed

• Success = on each trial, the probability  p of success must be the same

Binomial formula

How to do (n/x) combination:

n → math → prob → nCr → x = answer

binompdf (n, p, x)

Finds the probability of getting an exact value out of n trials with probability p

binomcdf(n, p, x)

Finds the probability of getting a value [at most X times / X times or less] out of n trials with probability p

Even though the probability of exactly 7 successes is tiny, the cumulative probability up to 7 includes all possible outcomes 0,1,2,…,70, 1, 2, …, 70,1,2,…,7, so it must add up to 1.

“The probability of having a cat is 0.3 What is the probability that exactly 5 people, out of 10, will have a cat.”

binompdf(10, 0.3, 5)

“The probability of having a cat is 0.3 What is the probability that at most 5 people, out of 10, will have a cat.”

binomcdf(10, 0.3, 5)

“The probability of having a cat is 0.3 What is the probability that between 4 and 7 people (inclusive), will have a cat.”

binomcdf(10, 0.3, 7) - binomcdf(10, 0.3, 3)

“The probability of having a cat is 0.3 What is the probability at least 5 out of 10 people will have a cat.”

1 - binomcdf(10, 0.3, 4)

You do 1 - (…) because the calculator only does X OR LESS. It cannot count up

Also you do 4 instead of 5 bc binom function is inclusive

Under what conditions is a normal distribution a good approximation to the binomial distribution?

• np ≥ 10

• n(1-p) ≥ 10

And in your sentence you have to say “therefore, using a normal distribution to approximate this binomial distrubition for this problem…”

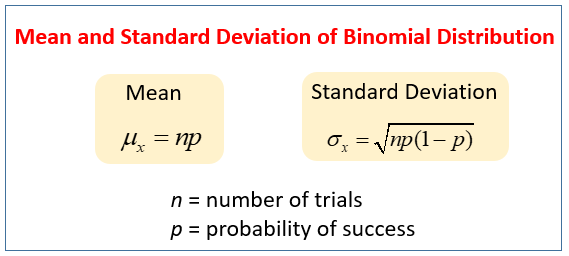
How to find mean and standard deviation of binary distribution

What is a geometric setting

A geometric setting arises when we perform independent trials of the same chance process and record the number of trials until the first success

Conditions for a geometric distribution

BITS

• B = binary (success or fail)

• I = independent

• T = stops after a success

• S = on each trial, the probability p of success stays constant

Rule for calculating geometric probabilities

P(X = n) = p(1 - p)^n-1

This is essentially the multiplication rule; imagine landing on 5 for the first time on the 3rd roll of the die

(5/6)(5/6)(1/6) → multiplication rule!

The probability that it takes more than n trials to see the first success P(X > n)

P(X > n) = (1 - p)ⁿ

Mean and SD for geometric distribution

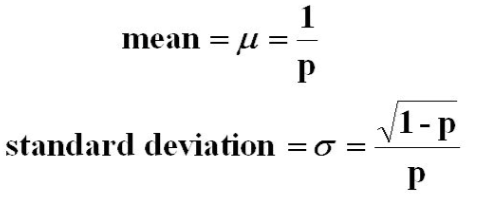
geometpdf(.5, 3)

What is the probability that a success (0.5 chance) occurs on exactly the 3rd trial

geometcdf(0.5, 3)

What is the probability that a success (0.5 chance) occurs on the 3rd or before

In a geometric distribution, which trial has the highest probability of success?

The first, since with each trial you are multiplying by a number < 1

Compare the shapes of the graphs of binomial distributions vs. geometric distributions

Identifying each distribution

excepts it’s just B and G