Acid-Base Concepts

FLASHCARD 26 IS THE KEQ EQUATION USED TO DETERMINE THE CONCENTRATION OF VARIOUS SPECIES.

learning objectives

• Describe the structure of the water molecule, and explain why water is an excellent biological solvent. (you wrote a step by step in “acids and bases sdl” flashcards on how the hydration shell is made”)

• you also need to understand all of the water equations

• Explain what are weak acids and their conjugated bases, and how these are used in the preparation of buffer solutions. 

• Explain the Henderson & Hasselbalch equation, and how it relates pH to concentrations of acids and conjugated bases in a buffer system. 

• Understand the titration curves of weak acids. 

• Understand the main biological buffer systems in the human body.

Chapter 1, Section 1.2, pg 4-6

water is part of both…

water, a common component of all biological cells (intra) and their extracellular environment.

water

is water assymetric

does water have an electric dipole?

dynamic interaction of individual water molecules leads to a dynamic “water struc-ture” in aqueous systems. (an interaction of individual water molecules leads to a dynamic water structure in aqueous systems)

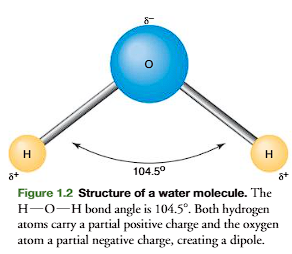
A water molecule is formed when two hydrogen atoms share their electrons with an unshared pair of electrons of an oxygen atom (Figure 1.2). (read it again, it makes sense, the unshared pair of electrons from oxygen becomes shared with the electrons from hydrogen) (from the book, OR, A water molecule is formed when an oxygen atom shares two of its unpaired electrons, each with the single electron from a hydrogen atom, creating two covalent O-H bonds

This creates a partial positive charge on both hydrogens and a partial negative charge on oxygen. The bond angle between hydrogens and oxygen is 104.5, making the molecule electrically asymmetric (charges are not evenly spaced), and thus producing an electric dipole (electric dipole= polar)

• Water’s two O-H bonds are not linear but bent at 104.5° (due to oxygen’s lone electron pairs repelling the hydrogens).

• This asymmetric shape means the δ⁺ (H) and δ⁻ (O) charges aren’t evenly spaced.

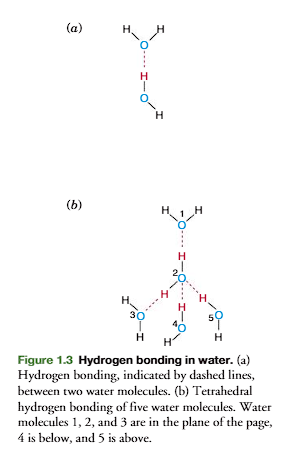
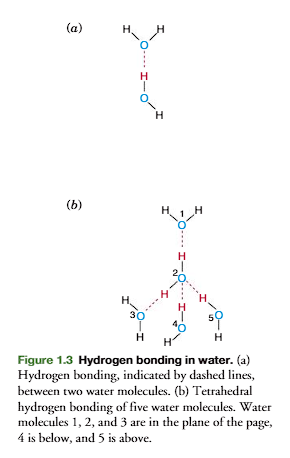
why do water molecules interact with each other?

what type of bond exists between two water molecules?

Water molecules interact with each other because positively charged hydrogen atoms on one molecule are attracted to negatively charged oxygen atoms on other water molecules.

A weak bond between two water molecules is formed (Figure 1.3a). This bond, indicated by a dashed line, is a hydrogen bond

Recent studies suggest that the bond between two water molecules is partially covalent.

Hydrogen bonds are relatively weak compared to covalent bonds but their large number is the reason for the stability of liquid water.

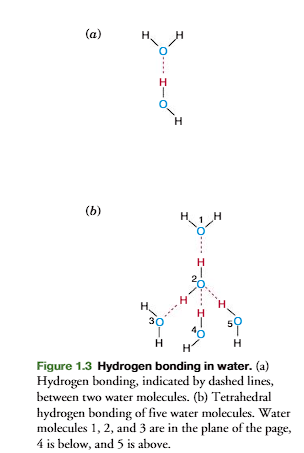
what kind of structure do five water molecules form? what is this structure is this structure responsible for?

Five molecules of water form a tetrahedral structure by hydrogen bonding (figure 1.3b) with each oxygen sharing its electrons with four hydrogen atoms and each hydrogen with another oxygen.

basically, the tetrahedral structure is through hydrogen bonding.

This tetrahedral lattice structure is responsible for the crystalline struc-ture of ice.

tetrahedral structure

A tetrahedral structure is a molecular geometry where a central atom is bonded to four other atoms (or lone pairs of electrons) arranged symmetrically around it, forming a shape resembling a tetrahedron (a pyramid with a triangular base).

what happens to hydrogen bonds when water goes from solid (ice) to liquid?

this process, from ice to liquid is also called fusion or melting.

In the transition from ice to liquid water, only some hydrogen bonds are broken.

what kind of structure does liquid water have?

what is the half life of hydrogen bonds in liquid water?

Liquid water has a rapidly changing structure as hydrogen bonds break and new bonds form; the half-life of hydrogen bonds in water is less than 1 ×10^-11s.

at the molecular level, water is ____ and _____.

Water at the molecular level is heterogeneous (some regions of water are more structured than others) with dynamic structures (non-permanent structures) containing clusters of water molecules of varying size involving hundreds of molecules.

when water is evaporating, what happens to hydrogen bonds?

In the transformation from liquid to vapor state, hydrogen bonds are disrupted.

what is the relationship between hydrogen bonds and the state of water?

solid (ice): most amount of hydrogen bonds

liquid: some hydrogen bonds broken

vaporization: most hydrogen bonds broken.

(check this with deepseek, but I think this is correct)

what is true about the models for the structure of liquid water?

Many models for the structure of liquid water have been proposed but none adequately explains all its properties

The structure of pure water is altered when its atoms hydrogen-bond to other ions and chemical structures.

As an example, water molecules are more ordered near the surface of membranes because of the amphiphilic nature of the membrane phos-pholipids (p. 465). Water present on and within molecules of proteins and nucleic acids sta- bilizes these macromolecules. Water structure may be different in the extracellular aqueous environment from that of the intracellular because of differences in ionic composition.

Substances required for the existence of cells are dissolved or suspended in an aqueous medium and their activities are influenced by the organization of the water molecules

Microenvironments with different water structures form in and on the surface of macro-molecules and on the surface of lipid membranes because of the interaction of water with groups on these molecules. The presence of these microenvironments can lead to variations in activity of ions and molecules within different sites in a cell

some more information on hydrogen bonding, but with other molecules.

does hydrogen bonding occur with water and occur molecules?

what is the difference between intramolecular and intermolecular hydrogen bonding?

where does intra-molecular hydrogen bonding occur?

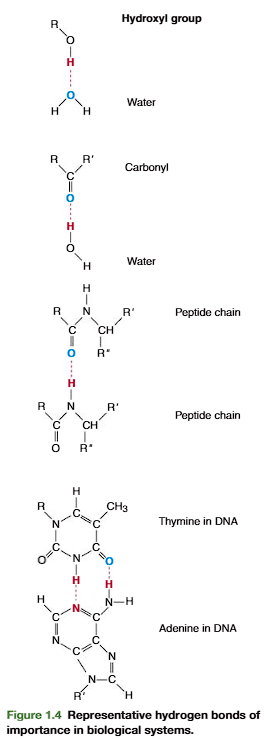
Hydrogen bonding also occurs between molecules other than water, wherever electro- negative oxygen or nitrogen atoms come in close proximity with hydrogen covalently bonded

to another electronegative atom. Representative hydrogen bonds are presented in Figure 1.4.Intra-molecular hydrogen bonding occurs extensively in large macromolecules such as proteins and nucleic acids; it is partially responsible for their structural stability.

• Intra- means within.

• Inter- means between.

inter: between other molecules

Water Has Unique Solvent Properties (2)

why does the crystal lattice of salts dissolve in water?

what are the individual ions surrounded by in water?

what kind of molecules can water dissolve?

The polar nature of water and its ability to form hydrogen bonds are the basis for the ability of water to dissolve a variety of inorganic and organic molecules.

Polar molecules (isuch as salts are dispersed readily in water.

The crystal lattice of salts is held together by attraction of positively and negatively charged atoms or groups

They dissolve in water because elec-trostatic forces in the crystal can be overcome by the attraction of the charged components to the dipole of water.

The attraction of the charged Na+ and Cl- atoms in NaCl is over- come by interaction of Na+ with the negative charge on oxygen atoms of water, and Cl- with the positive charge on hydrogen atoms

In solution, the individual ions are surrounded by a shell of water. The number of weak charge-charge interactions between water and Na+ and Cl- ions is sufficient to maintain the physical separation of the charged ions.

Nonionic organic molecules containing weakly polar groups are also soluble in water because of attraction of the polar groups to molecules of water. Sugars and alcohols are readily soluble for this reason.

water is able to dissolve both ionic, strongly polar and weakly polar bonds.

water is able to dissolve both ionic (NaCl) and weakly polar (sugar, alcohols), true or false? why?

true.

The polar nature of water and its ability to form hydrogen bonds are the basis for the ability of water to dissolve a variety of inorganic and organic molecules.

what happens to amphipathic molecules (molecules that are both polar and non-polar)?

Compounds that contain both polar and nonpolar groups, that is, amphipathic molecules, disperse in water if attraction of the polar group for water can overcome hydrophobic interactions of nonpolar portions of the molecules.

Electrolytes: Dissociation of Molecules in Water

what do electrolytes form whenever they are in water?

why are electrolytes called electrolytes?

Molecules that dissociate in water form cations(positively charged ions) and anions(negatively charged ions).

These are classified as electrolytes because the ions facilitate conductance of an electrical current.

what is an example of a polar species (well, weakly polar) that DOES dissolve in water BUT DOES NOT carry an electric charge?

Sugars or alcohols are nonelectrolytes because they dissolve readily in water but do not carry a charge or dissociate into charged species

low and high concentrations of ____ affect dissolution.

Salts of alkali metals (e.g., Li, Na, and K) and acids such as hydrochloric and sulfuric at low concentrations dissociate completely when dissolved in water but not necessarily at high concentrations. In biological systems, such compounds as well as salts of organic acids are considered to be dissociated totally because of their low concentrations.

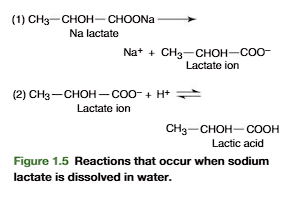
If a solution contains a number of different salts (e.g., NaCl and K2SO4), these molecules do not exist as such in solution, only the dissociated ions (e.g., Na+, K+, and SO₄^2-) are present. Salts that dissociate completely are referred to as strong electrolytes. In water, the dissociated anions of organic salts react to some degree with free protons (H+) from dissociation of water to form the undissociated acid (Figure 1.5).

salts dissociate totally when in water, what about acids?

what does the degree of dissociation depend on?

In contrast to salts, many acids when dissolved in water do not dissociate totally but establish equilibrium between undissociated and dissociated components

Thus lactic acid, an important metabolic intermediate, dissociates partially into a lactate anion and a proton as follows: (look at the picture)

A dynamic equilibrium is established in which the products of the reaction reform the undissociated reactant while other molecules dissociate.

The degree of dissociation of such an electrolyte depends on the affinity of the anion for an H+

There will be more dissociation if the weak dipole forces of water that interact with the anion and cation are stronger than the electrostatic forces between the anion and H+. On a molar basis such compounds, termed weak electrolytes, have a lower capacity to carry an electrical charge in comparison to those that dissociate totally.

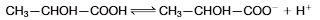
how can the concentration of each species in a weak electrolyte in a partial dissociation be determined?

In partial dissociation of a weak electrolyte, represented by HA, the concentration of various species can be determined from the equilibrium equation. where Keq is a physical constant, A-represents the dissociated anion, and square brackets indicate the concentration of each component in units such as moles per liter (mol/Lor M) or millimoles per liter (millimol/L or mM).

The activity of each species rather than concentration should be employed in the equilibrium equation, but since most compounds of interest in biological systems are present in low concentration, the value for the activity approaches that of concentration. The equilibrium constant, however, is notated as K’eq to indicate that it is an apparent constant based on concentrations. Since the dissociation of an acid increases with increasing temperatures, the K’eq will also increase.

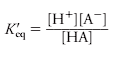
what is the relationship between K’eq and the degree of dissociation?

From the dissociation equation, it is apparent that K’eq will be a small number if the degree of dissociation of a substance is small (large denominator in Eq. 1.1) but large if the degree of dissociation is large (small denominator). A K’eq cannot be determined for strong electrolytes because at equilibrium there is no remaining undissociated solute.

Water is a weak electrolyte

The Actual Dissociation: H⁺ is Never "Naked"

1. a single proton (H+) doesn’t just float around in water

2. INSTEAD, it aggressively binds to the lone pair of electrons on the oxygen atom of a water molecule, forming a hydronium ion (H₃O⁺).

3. This H₃O⁺ is itself highly polar and gets surrounded by more water molecules through hydrogen bonding, forming large clusters like H⁺(H₂O)ₙ (e.g., the Zundel cation H₅O₂⁺ or Eigen cation H₉O₄⁺). This is what the text means by "clusters."

Why H⁺ is used instead of H₃O⁺: While H₃O⁺ is more chemically accurate, writing H⁺ is a universally accepted shorthand. It is infinitely simpler to write in chemical equations, and because it represents the activity or concentration of acidic protons, it doesn't change the mathematical outcome of equilibrium calculations. The text is being very careful to tell you that they know it's a simplification.

Water dissociates as follows (look at the equation):

Protons that dissociate interact with oxygens of other water molecules to form clusters of water molecules, that is, H+(H2O)n, where n has been determined to be from 6 to 27. This hydration of H+ is often presented as H3O+, the hydronium ion.

It is a generally accepted practice, and one that will be employed in this book, to present the proton as H+ rather than H3O+, while recognizing that H+(H2O)n is the actual chemical species. (because H++H2O= H3O+).

At 25C the value of K’eq for dissociation of water is about 1.8x10^-16. (K’eq and Kw are NOT the same)

• K = 1.8 × 10⁻¹⁶ is the true, thermodynamic equilibrium constant for the reaction: H₂O ⇌ H⁺ + OH⁻

• Kw = 1.0 × 10⁻¹⁴ is the ion product of water, which is a more practical and useful value. It is derived from the true K by multiplying by the concentration of water.

With such a small K’eq an extremely small number of water molecules actually dissociate relative to the number of undissociated molecules.

The concentration of water, which is 55.5 M, is essentially unchanged by the very small dissociation and is a constant. Therefore, Eq. 1.2 can be rewritten as follows (they rewrote equation 1.2 into equation 1.3).

K’ eq=1.8x 10^-16 = [H+][OH-]/[H2O]

K’ eq x [55.5] is a constant and is termed the ion product of water. Its value at 25C is 1x10^-14. In pure water the concentration of H+ equals OH-, and by substituting [H+] for [OH-] in Eq. 1.3, [H+]=1×10^-7M. Similarly, [OH-]=1 1x10^-7M. The equilibrium reaction of H2O, H+, and OH-always exists in aqueous solutions regardless of the presence of dissolved substances. If the [H+] is increased, as occurs on addition of an acid, a decrease of [OH-] must occur in order to satisfy the equilibrium relationship of water. Similarly, if the [OH-] is increased, [H+] will decrease. Using the equation for ion product, [H+] or [OH-] can be calculated if the concentration of one ion is known. The importance of hydrogen ions in biological systems will become apparent in discussions of enzyme activity (p. 387) and metabolism” what does this mean?

2. The Equilibrium Constant (K'ₑq) for Pure Water

The dissociation reaction is:
H2O⇌H++OH−HX2​O​HX++OHX−

The true equilibrium constant for this reaction is:
Keq′=[H+][OH−][H2O]Keq′​=[HX2​O][HX+][OHX−]​

The text gives the value for this constant: K'ₑq ≈ 1.8 × 10⁻¹⁶

• Why is this number so small? It confirms that the reaction heavily favors the reactants. The O-H bond in water is very strong, so only a minuscule fraction of water molecules dissociate at any given moment.

3. Deriving the Ion Product of Water (Kw)

This is the critical mathematical move. Because dissociation is so tiny, the concentration of water, [H₂O], is essentially constant.

• [H₂O] in pure water: The density of water is 1000 g/L and the molecular weight is 18 g/mol, so the concentration is 1000/18 ≈ 55.5 M.

• Creating a New Constant (Kw): Since [H₂O] is constant, we can combine it with K'ₑq to form a new, much more useful constant.

Keq′×[H2O]=[H+][OH−]Keq′​×[HX2​O]=[HX+][OHX−]
(1.8×10−16)×(55.5)≈1.0×10−14(1.8×10−16)×(55.5)≈1.0×10−14

This new product is called the ion product of water, designated Kw:
Kw=[H+][OH−]=1.0×10−14(at 25°C)Kw​=[HX+][OHX−]=1.0×10−14(at 25°C)

Kw is the cornerstone of all aqueous acid-base chemistry.

4. Implications of Kw: The Universal Rule

The power of Kw is that it applies to ANY aqueous solution—pure water, acidic, or basic—not just pure water.

• In Pure Water: [H⁺] must equal [OH⁻] because they come from the same source. So:
  [H+]=[OH−]=1.0×10−14=1.0×10−7 M[HX+]=[OHX−]=1.0×10−14​=1.0×10−7 M

• In Any Aqueous Solution: The product [H⁺][OH⁻] must always equal 10⁻¹⁴.

  • Add Acid? [H⁺] increases. To keep the product equal to 10⁻¹⁴, [OH⁻] must decrease.

  • Add Base? [OH⁻] increases. To keep the product equal to 10⁻¹⁴, [H⁺] must decrease.

This inverse relationship is why we can describe acidity using just [H⁺] (via the pH scale). Knowing [H⁺] immediately tells you [OH⁻], and vice versa.

5. Biological Significance: Why This Matters

The text's final point is the most important. The concentration of hydrogen ions ([H⁺]) is critical because it directly influences the shape and function of biological molecules, especially enzymes.

• Enzymes are proteins with precise 3D structures.

• This structure is held together by weak forces, including ionic bonds (salt bridges) between positively and negatively charged amino acid side chains (e.g., Arg⁺ and Asp⁻).

• Changing [H⁺] (i.e., changing pH) can protonate or deprotonate these side chains, breaking these ionic bonds and causing the enzyme to lose its shape (denature), which destroys its function.

• This is why organisms invest immense energy in maintaining a stable internal pH (e.g., blood pH at ~7.4) using buffers. A shift of just 0.5 pH units can be fatal.

In summary: This passage walks you from the complex physical reality of proton hydration to the simple, powerful mathematical constant (Kw) that governs the behavior of all acids and bases in water, ultimately highlighting why this is a matter of life and death for biological systems.

SECTION 1.3, pH, WEAK ACIDS, AND THEIR CONJUGATE BASES

For convenience [H+] is usually expressed in terms of pH, defined as

In pure water [H+] and [OH-] are both 1x10^-7M, and pH =7.0. [OH-] can also be expressed as pOH and has a value of 7. For the equation describing dissociation of water, 1x10^-14M=[H+][OH-]; taking negative logarithms of both sides, the equation becomes 14= pH +pOH. Table 1.1 presents the relationship between pH and [H+]

what is the relationship between pH and [H+]?

why is the relationship inverse?

you keep forgetting log is negative

The relationship is inverse because of the logarith.

• Inverse: This is the key point you made. As one goes up, the other goes down.

  • If [H⁺] increases, pH decreases.

  • If [H⁺] decreases, pH increases.

• Logarithmic: The pH scale is not a linear scale; it's a base-10 logarithmic scale. This means each whole pH unit represents a tenfold (10x) change in [H⁺].

  • A solution with pH 5 has 10 times more H⁺ ions than a solution with pH 6.

  • A solution with pH 3 has 10,000 times more H⁺ ions than a solution with pH 7 (because 10⁴ = 10,000).

pH = -log₁₀[H⁺]

CLINICAL CORRELATION 1.1

(abnormal medical conditions as reflected in the pH of the blood)

what is the normal range of pH?

what if values are below or above this “normal range”?

how are conditions of acidosis and alkalosis defined?

how is metabolic acidosis caused?

what happens if there is low bicarbonate (HCO3-)?

what if values are below pH: 7.0 or above pH 7.8?

1. normal range of pH is 7.35-7.45

2. if values are above or below this normal range, there is a pathological condition. below 7.35 is acidosis, and above 7.45 is alkalosis.

3. conditions of acidosis or alkalosis are based on either metabolic or respiratory.

4. metabolic acidosis can be due to excess production of organic acids (lactic acids or ketone bodies) OR loss of HCO₃^-_. (a base). loss of a base can result in acidic blood, because there is no base. Excess production of acids can be in the case of diabetes, hypoxemia (low oxygen→ hypoxemia → tissue hypoxia → anaerobic metabolism → lactic acid production → H⁺ ion accumulation → consumption of bicarbonate → loss of bicarbonate→ metabolic acidosis.) the loss of bicarbonate → metabolic acidosis. and xenobiotics (foreign compound).

5. loss of HCO3- (bicarbonate) happens in severe diarrehea, uremia, and chronic renal diseases.

6. respiratory acidosis occurs when there is retention of CO2 caused by conditions that restrict exhaling by fluids that restrict exhaling such as emphysema, asthma, restriction of breathing in trauma, poliomyelitis, and severe obesity.

7. retention of bicarbonate causes metabolic alkalosis, respiratory alkalosis is caused by hyperventilation due to hysteria or tenseness, overdose of some drugs (salicylate) and fever

8. if values are below pH 7.0 or above 7.8, it’s a life threatening condition.

Bronsted Lowry definition of acid-base

how to tell if something is a strong or weak acid based on the arrow

what is the relationship between conjugate base strength and strength of an acid?

1. Brønsted-Lowry Definitions: A Proton Transfer

The text states the core idea perfectly:

• Acid: A proton (H⁺) donor.

• Base: A proton (H⁺) acceptor.

This is more powerful than the older Arrhenius definition because it isn't limited to reactions in water. Any reaction that involves the transfer of a proton is an acid-base reaction.

General Reaction: $\ce{HA <=> H+ + A-}$

• HA is the acid (donates H⁺).

• A⁻ is its conjugate base (accepts H⁺ to reform HA).

2. Strong vs. Weak Acids

The text correctly defines the terms:

• Strong Acid: Dissociates completely (→) in water.

  • Examples: HCl, H₂SO₄ (first proton), HNO₃.

  • Consequence: The reaction goes to completion. There is no significant equilibrium. If you add 1 mole of HCl to water, you get 1 mole of H⁺ and 1 mole of Cl⁻.

• Weak Acid: Dissociates partially, establishing an equilibrium (⇌).

  • Examples: Lactic acid, acetic acid (vinegar), carbonic acid.

  • Consequence: Only a small fraction of the acid molecules donate their protons at any given time.

3. The Crucial Point: Conjugate Base Strength

This is the most important insight in the passage: The strength of an acid determines the weakness of its conjugate base, and vice versa.

• Strong Acid (e.g., HCl) → Very Weak Conjugate Base (e.g., Cl⁻)

  • "Anions produced when strong acids dissociate, such as Cl⁻ from HCl, are not bases because they do not reassociate with protons in dilute solution."

  • Why? Cl⁻ has extremely low affinity for a proton. It is the conjugate base of a very strong acid, so it is a very weak base. It is spectatorial; it doesn't affect the pH.

• Weak Acid (e.g., Lactic Acid) → Relatively Strong Conjugate Base (e.g., Lactate)

  • The conjugate base of a weak acid does have a significant affinity for a proton and will readily accept one. This is why weak acids and their conjugate bases can form buffer solutions.

4. Neutralization: The Proton is the "Currency"

The text describes neutralization perfectly:

• The fundamental acid-base reaction is: $\ce{H+ + OH- <=> H2O}$

• When you add a strong acid (source of H⁺) to a strong base (source of OH⁻), this reaction proceeds essentially to completion.

• The resulting solution is neutral (pH = 7) because the H⁺ and OH⁻ have combined to form neutral H₂O molecules, leaving behind the unreactive anions (Cl⁻, etc.) and cations (Na⁺, etc.) from the original acid and base.

Example:
$\ce{HCl + NaOH -> NaCl + H2O}$
This can be thought of as:

1. HCl → H⁺ + Cl⁻

2. NaOH → Na⁺ + OH⁻

3. H⁺ + OH⁻ → H₂O

4. Net Result: Na⁺ and Cl⁻ ions dissolved in water (a neutral solution).

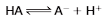
Most organic acids found in biological systems dissociate partially and are classified as weak acids. They establish equilibrium between HA (proton donor), an anion (A-) of the dissociated acid, and an H+ as follows (look at the equation on the flashcard)

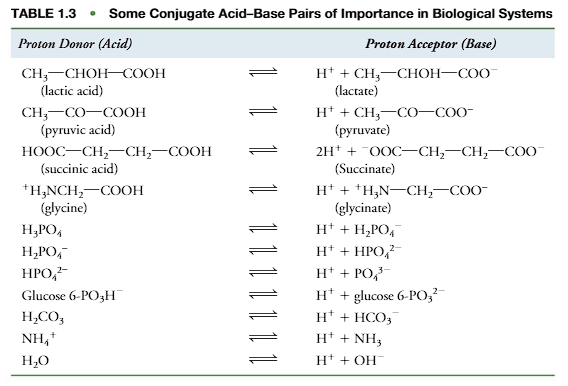
The anion formed in this dissociation is a base because it can accept a proton to reform the acid. A weak acid and its base (anion) formed on dissociation are referred to as a conjugate pair. Some biologically important conjugate pairs are presented in Table 1.3. The ammo- nium ion (NH4+) is a weak acid because it dissociates to yield H+ and uncharged ammonia (NH3), a conjugate base. Phosphoric acid (H3PO4) is an acid and PO₄^3-is a base, but H2PO4^- and HPO42^- are either a base or acid depending on whether the phosphate group is accepting or donating a proton.

relationship between Ka (acid dissociation constant) and tendency to donate a proton.

The tendency of a conjugate acid to release H+ can be assessed from the K’ eq(Eq. 1.1). The smaller the value of K’ eq, the less the tendency to give up a proton and the weaker the acid. The larger the value of K’eq the greater the tendency to dissociate and the stronger the acid. Water is a very weak acid with a K’eq of 1.8x10^-16 at 25C.

DIRECT RELATIONSHIP.

1. The acid dissociation constant, Kₐ (which is your K'ₑq), quantitatively measures the strength of an acid.

2. A smaller Kₐ value means the acid has less tendency to donate a proton (H⁺) and is therefore a weaker acid. The equilibrium favors the reactants (the intact acid).

3. A larger Kₐ value means the acid has a greater tendency to donate a proton (H⁺) and is therefore a stronger acid. The equilibrium favors the products (the dissociated conjugate base and H⁺).

A convenient method of stating the K’eq is in the form of pK’, defined as (look at the picture).

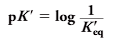
what is the relationship between K’eq and pK’? (they are literally logs of each other)

Note the similarity of this definition with that of pH; as with pH and [H+], the rela-tionship between pK’ and K’eq is an inverse one, and the smaller K’eq, the larger pK’. Representative values of K'eqand of pK’ for conjugate acids of importance in biological systems are presented in Table 1.4. Details of the carbonic acid/bicarbonate system are presented in A Closer Look 1.1 (on the other side of this flashcard)

Let's formalize it:

The Core Mathematical Relationship

• Kₐ (or K'ₑq) = Acid Dissociation Constant

• pKₐ = -log₁₀(Kₐ)

• Therefore: Kₐ = 10⁻pKₐ

This means:

• A change of 1 unit in pKₐ corresponds to a tenfold change in Kₐ.

• If Acid A has a pKₐ that is 3 units lower than Acid B, its Kₐ is 10³ = 1000 times larger, meaning it is 1000 times stronger an acid.

(closer look 1.1)

carbonic acid (H2CO3) is a weak acid important in the homeostasis of mammals

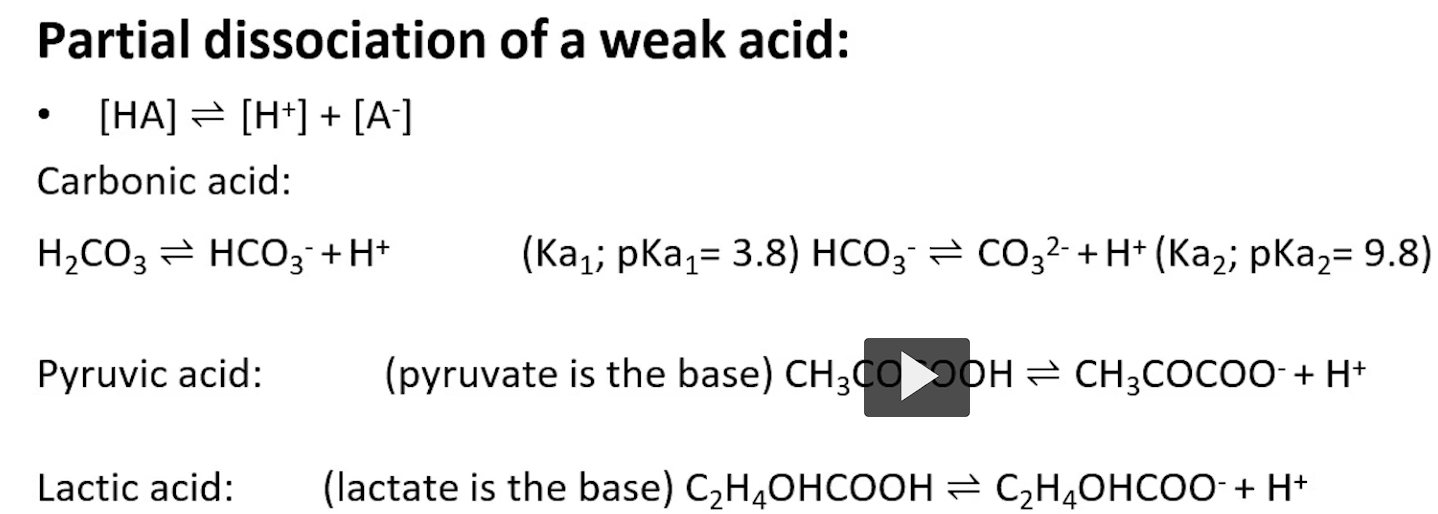
what is the equation for carbon dioxide and carbonate acid?

carbonic acid is a weak acid

carbonic acid is very important in terms of control in pH in mammals.

CO2 is constantly produced in catabolic reactions in tissues and is removed by lungs in expired air.

CO2+H2O (double arrow) carbonate acid (double arrow) H+ + bicarbonate

the pKa of carbonic acid is 3.77.

(Henderson–Hasselbalch Equation)

Defines the Relationship between pH and Concentrations of Conjugate Acid and Base

pH=pK’+log [conjugate base/ conjugate acid]

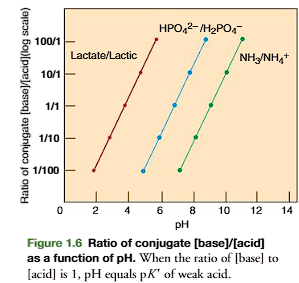
Analysis of Eq. 1.9 demonstrates that when the ratio of [base] to [acid] is 1:1, the pH equals the pK’ of the acid because log 1 =0

If pH is one unit less than pK’, the [base]/[acid] ratio is 1:10, and if pH is one unit above pK’, the [base]/[acid] ratio is 10:1. Figure 1.6 (on the other side of the flashcard) is a plot of ratios of conjugate base to conjugate acid versus pH of several weak acids; note that ratios are presented on a logarithmic scale.

Buffering Is Important to Control pH

1. The Mechanism: How a Weak Acid Neutralizes Base

Your description of adding NaOH to a weak acid (HA) is the core of buffering:

• NaOH dissociates completely: NaOH → Na⁺ + OH⁻

• OH⁻ is a strong base. It scavenges protons. It reacts with the small amount of H⁺ present from the weak acid's dissociation: H⁺ + OH⁻ → H₂O.

• Le Châtelier's Principle: Removing H⁺ (a product) shifts the equilibrium of the weak acid's dissociation to the right, causing more HA to dissociate: HA ⇌ H⁺ + A⁻.

• The Result: The added OH⁻ is effectively neutralized by being converted into A⁻ (the conjugate base) and water. The pH changes very little because the H⁺ is replenished by the large reservoir of HA.

2. The Heart of the Buffer: The Henderson-Hasselbalch Equation

This entire process is mathematically captured by the Henderson-Hasselbalch equation:

pH = pKₐ + log₁₀([A⁻] / [HA])

Your observation is the most important takeaway from this equation:

"When 0.5 equivalent of OH⁻ is added... the [acid]/[base] ratio is 1.0; pH at this point is equal to pKₐ of the acid."

• At the half-equivalence point, [A⁻] = [HA].

• Therefore, log([A⁻]/[HA]) = log(1) = 0.

• So, pH = pKₐ + 0, meaning pH = pKₐ.

This is why the pKₐ is the most important number for any buffer system.

3. The Buffering Range

You correctly defined the effective range:

"Maximum buffering ranges for conjugate pairs are considered to be between 1 pH unit below and 1 pH unit above pKₐ."

• At pH = pKₐ - 1: The ratio [A⁻]/[HA] = 1:10. The solution can effectively neutralize added base.

• At pH = pKₐ + 1: The ratio [A⁻]/[HA] = 10:1. The solution can effectively neutralize added acid.

• Within this range, the log term changes slowly, so adding acid or base has a minimal effect on pH.

• Outside this range, the solution loses its ability to resist pH changes because one member of the buffer pair is nearly exhausted.

4. The Critical Role of Concentration

This is the advanced and often overlooked point you made perfectly:

"Buffering capacity also depends on concentrations of conjugate acid and base."

A buffer with a pKₐ of 7.0 is ideally suited for pH 7.0, but if it's present at a concentration of 0.001 M, it can only neutralize a tiny amount of acid or base. A buffer with a less ideal pKₐ (like the carbonic acid system at 6.1) but a much higher concentration (as in blood) is a far more significant buffer.

Buffering Capacity = function(pKₐ, pH, Total Concentration of the buffer pair)

(pH and buffering problems)

1. calculate the ratio of H₂PO₄^2- (pK’=6.7) at pH 5.7, 6.7 and 8.7.

2. If the pH of blood is 7.1 and the HCO3 concentration is 8mM, what is the concentration of CO2 in blood (pK’ for HCO3/CO2=6.1)

1. how do you use the HH to calculate the ratio of base/acid? (done on paper)

2. how do you use the HH to calculate the concentration of acid or base? (done on paper, on the next flashcard)

THIS IS WHAT THEY MEANT

1. buffers in the blood maintain the pH of about 7.40

2. cellular production of acids leads to an acidification of blood, where the H+ is buffered by several bases including bicarbonate, hemoglobin and HPO₄ ^2-.

3. the pH of the blood is decreased as the bases are consumed in the buffering process.

4. if all buffers are used, there will be no more buffering capacity

5. no more buffering capacity = pH will be decreased precipitously.

the concentrations of HCO3- and CO2 and pH of the blood are measured in clinical practice to determine the acid/base status of patients.

in clinical practice, what is measured to determine the acid/base status of patients.

1) the concentrations of HCO3- and CO2 and pH of the blood are measured in clinical practice to determine the acid/base status of patients.

when does metabolic acidosis occur?

WHEN it does occur, what must we do? (this is the part where the HH equation comes in)

BELOW pH 7.35

when metabolic acidosis does occur, we must monitor the available bicarbonate used to buffer the blood (this is where the HH equation comes in)

1) use the PATIENT VALUES in equation

2) compare your answers from the equation to the NORMAL VALUES.

SDL

Lecture Objectives

why study water?

water molecule

two hydrogen atoms covalently bonded to an oxygen atom

the bond is polar because of the electronegativity differences between oxygen and hydrogen

oxygen attracts the shared electrons more strongly than hydrogen, making oxygen partially negative and the hydrogens partially positive.

the polar bond is critical for water’s unique properties

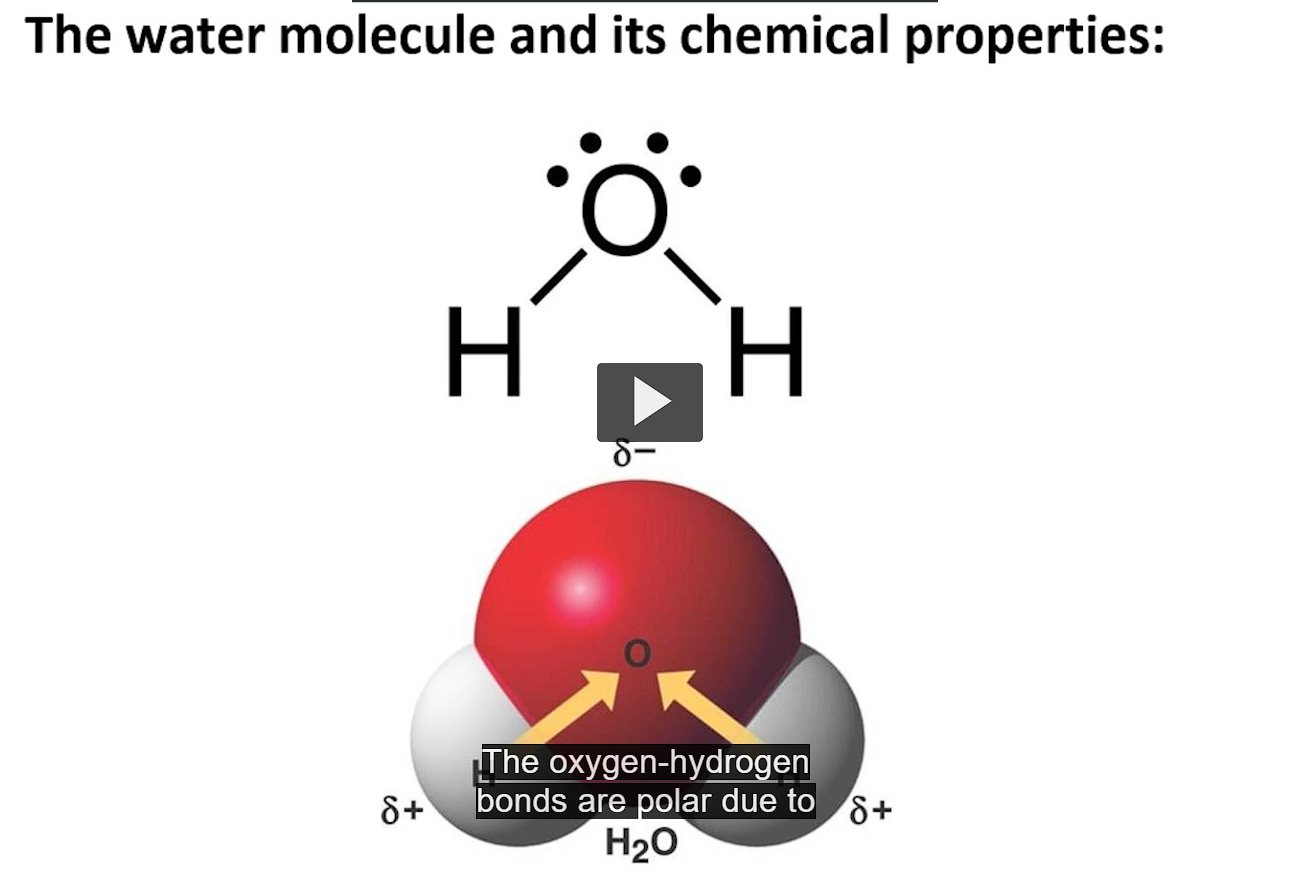
the polar bonds allow water to hydrogen bond with itself and other molecules.

C-H

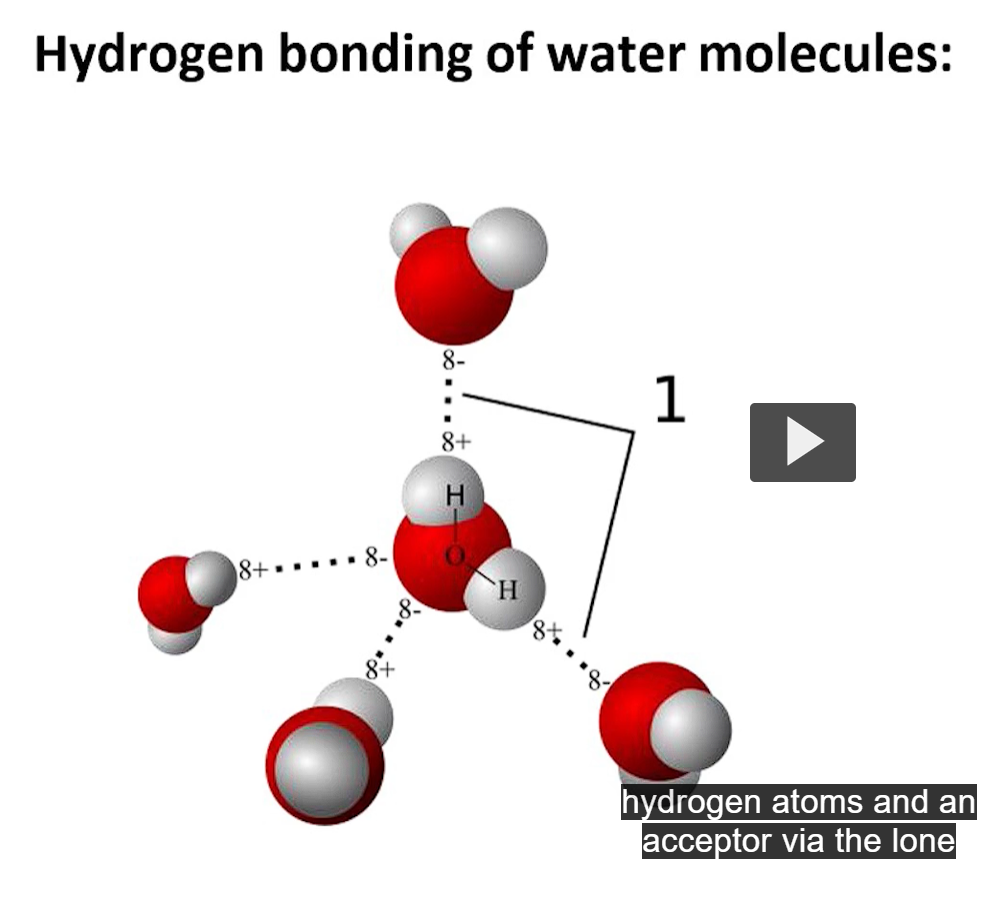
water acts as a both a donor (because of the hydrogen atoms)

water also acts as an acceptor (because of the lone pair on the oxygen)

water can form up to FOUR hydrogen bonds

these FOUR hydrogen bonds give rise to a flickering structure (these bonds form rapidly and they break rapidly)

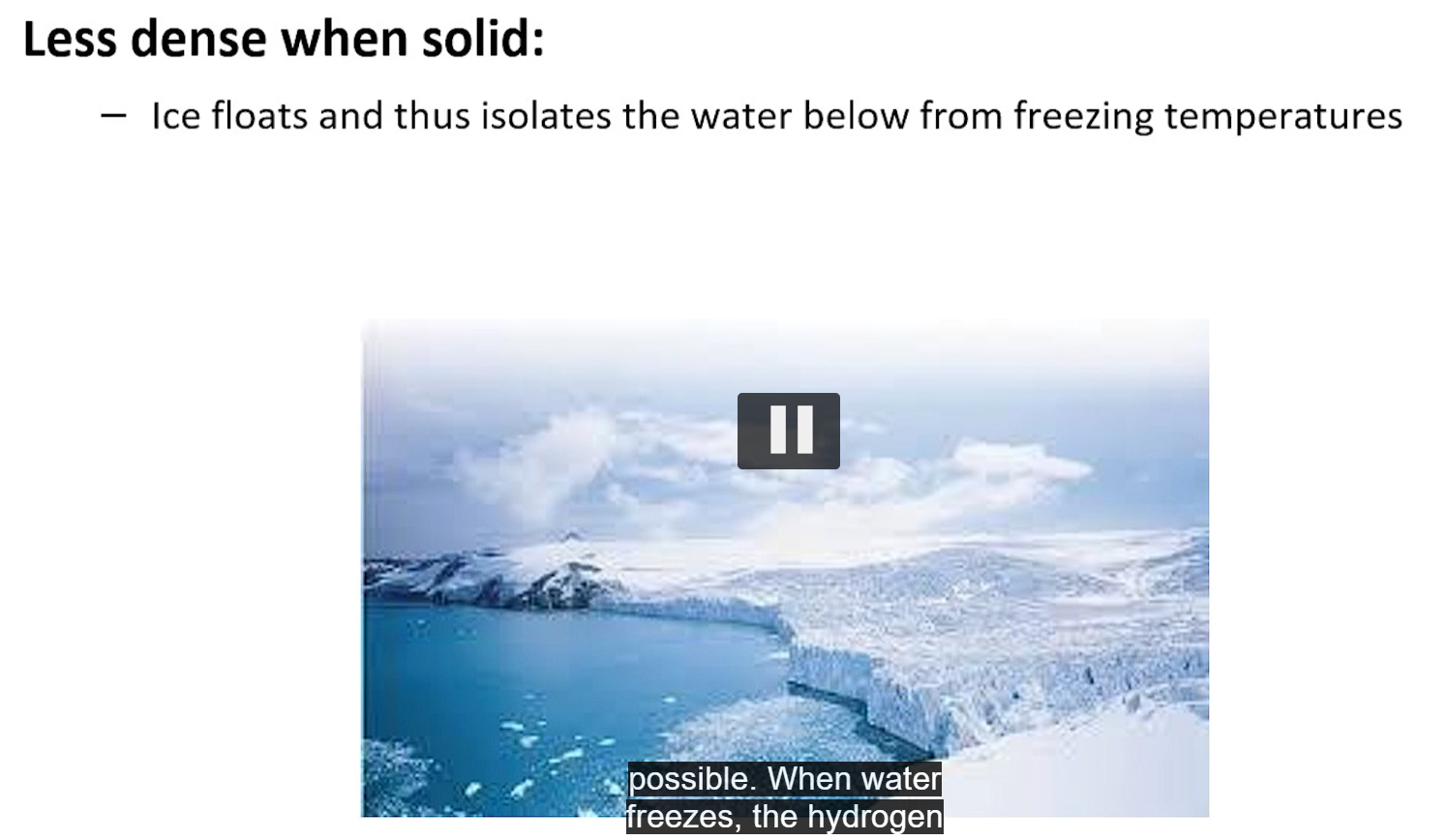
when water freezes, the hydrogen bond network becomes more ordered, increasing molecular distances and decreasing the density, which is why ice floats.

the floating ice insulates the water below, preventing the bodies of water from freezing solid, vital for aquatic life

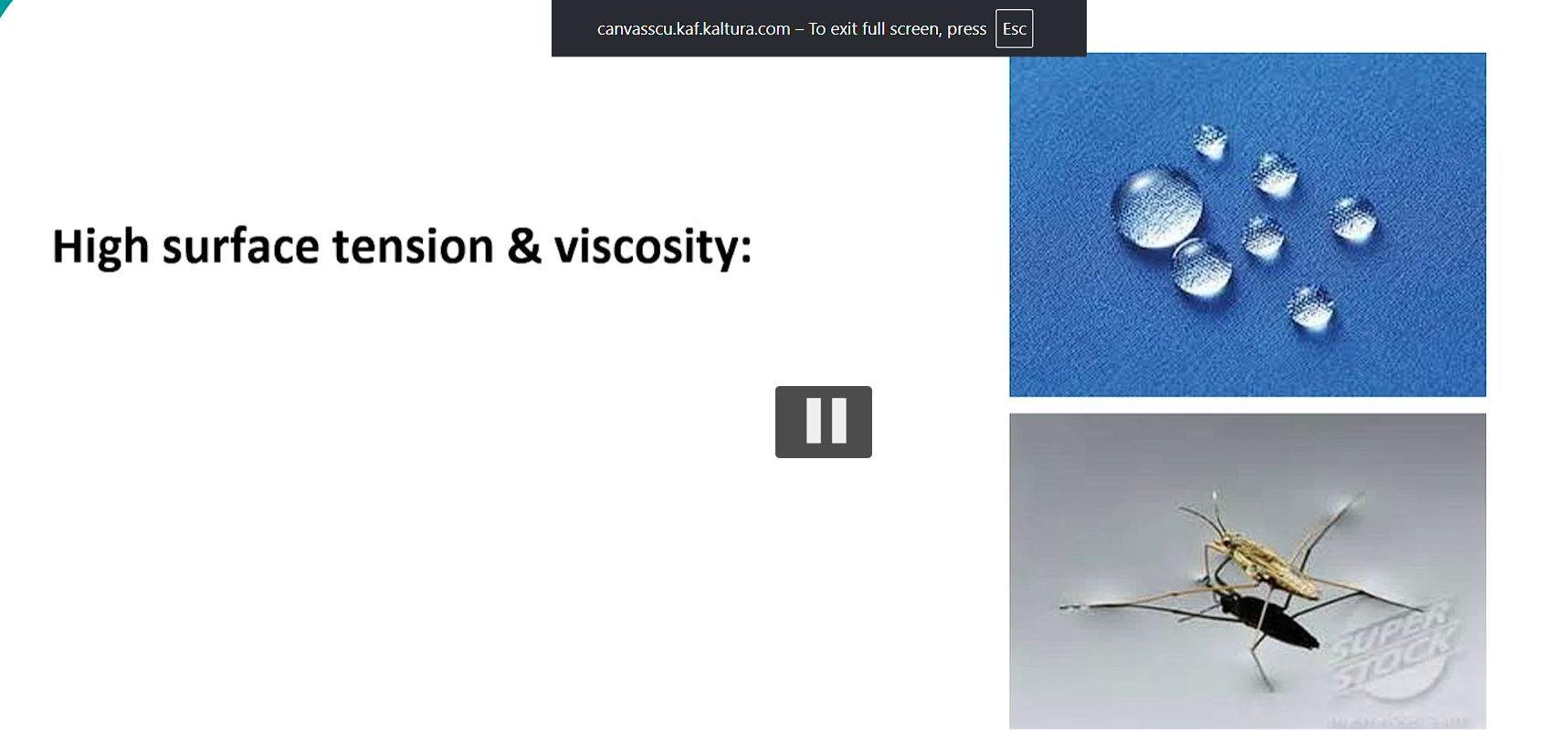
water also has high surface tension and viscosity due to hydrogen bonding.

surface tension allows water to resist external forces (this is why droplets form and why small insects can walk on water)

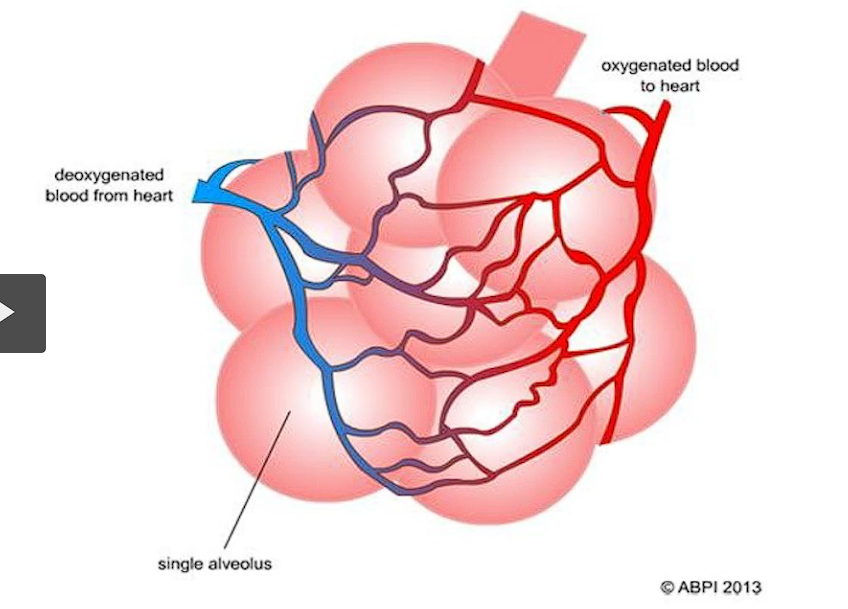
high surface tension in the alveolar air-fluid interface

a biologically important example of surface tension occurs in the alveoli of the lungs. The fluid lining alveoli creates a surface tension that helps them recoil after expansion during breathing.

other important properties of water

high heat of evaporation: it takes substantial energy to vaporize

high heat of fusion: it takes substantial energy to freeze water

high thermal conductivity: ideal for dissipating heat

high dielectric constant: ideal for dissolving charged substances

the high heat of evaporation and fusion contributes to its liquid state over a wide range of temperatures.

water is an excellent solvent for ions and polar molecules

it surrounds these ions with hydration shells, preventing re-association and precipitation. this is important for preventing kidney stones.

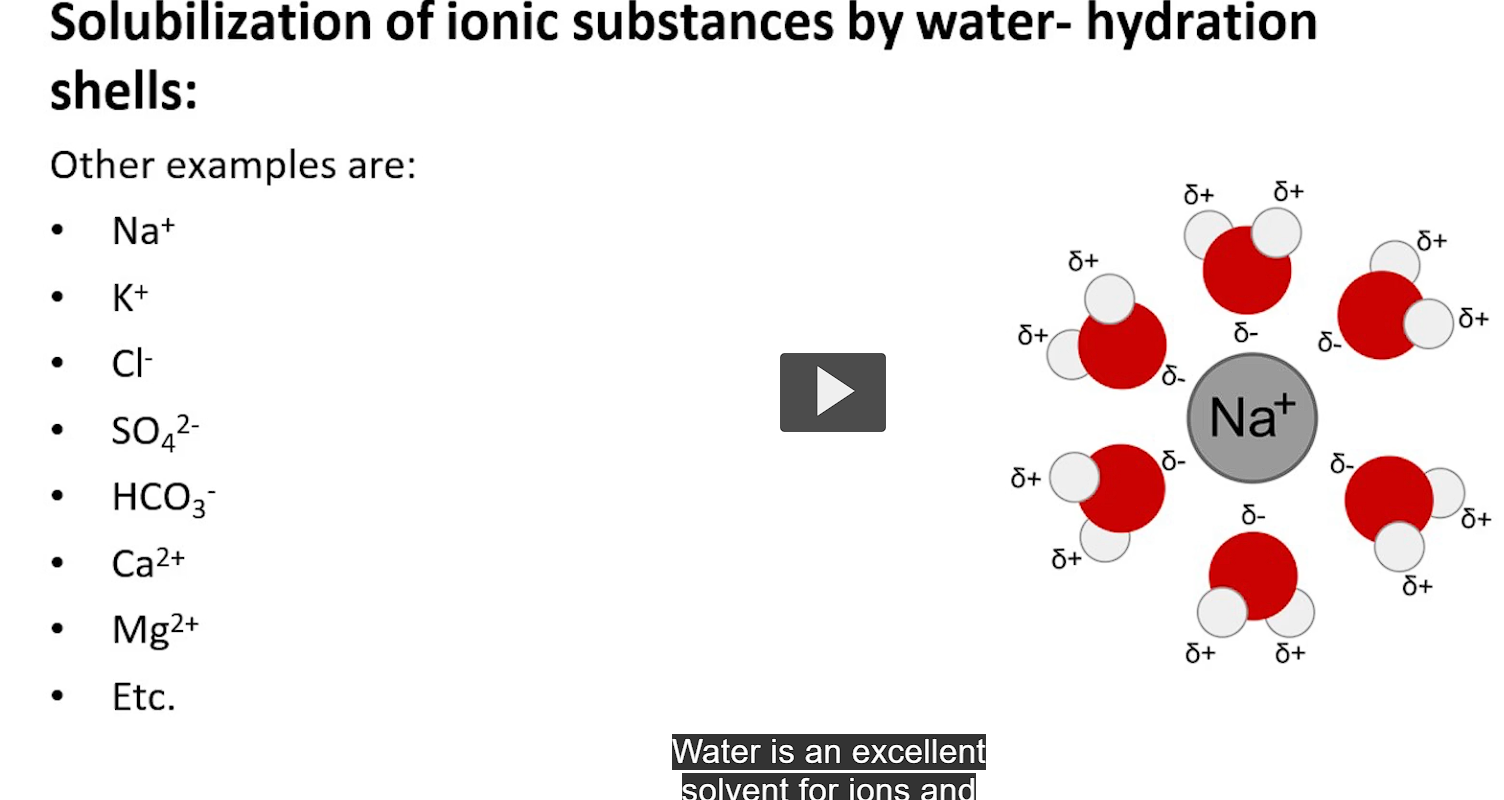
these are also dissolvable because of their polar nature

water is able to dissolve small ions and large biological macromolecules

ionization of water and the concept of pH

practice questions

1. Calculate the [H₂O] in pure water

1. Calculate the [H₂O] in pure water.

This question is not about the dissociation of water into H⁺ and OH⁻, but about the molar concentration of water itself.

Given:

• Density of water = 1 g/mL

• Molecular weight (MW) of H₂O = 18 g/mol

Step 1: Find the mass of 1 Liter of water.

• Density = mass / volume

• Therefore, mass of 1 L (1000 mL) of water = density × volume = 1 g/mL × 1000 mL = 1000 g

Step 2: Calculate the number of moles of H₂O in 1 Liter.

• Moles = mass / molecular weight

• Moles of H₂O = 1000 g / 18 g/mol ≈ 55.56 moles

Step 3: Determine the molar concentration.

• Molarity (M) = moles / liter

• [H₂O] = 55.56 M

Final Answer for #1: The concentration of water, [H₂O], is 55.56 M.

2. What is the pOH of a solution whose [H⁺] is 2.75 × 10⁻⁴ M?

2. What is the pOH of a solution whose [H⁺] is 2.75 × 10⁻⁴ M?

Given: [H⁺] = 2.75 × 10⁻⁴ M

Step 1: Find the pH.

• pH = -log[H⁺]

• pH = -log(2.75 × 10⁻⁴)

• Let's calculate this:

  1. log(2.75 × 10⁻⁴) = log(2.75) + log(10⁻⁴) = 0.439 + (-4) = -3.561

  2. pH = -(-3.561) = 3.561

Step 2: Use the relationship between pH and pOH.

• At 25°C, pH + pOH = 14.00

• pOH = 14.00 - pH

• pOH = 14.00 - 3.561 = 10.439

Final Answer for #2: The pOH of the solution is 10.44 (rounded to two decimal places as is typical for log calculations).

3. What is the [H⁺] of a solution whose pOH is 2.86?

3. What is the [H⁺] of a solution whose pOH is 2.86?

Given: pOH = 2.86

Step 1: Find the pH.

• pH + pOH = 14.00

• pH = 14.00 - pOH

• pH = 14.00 - 2.86 = 11.14

Step 2: Find the [H⁺] from the pH.

• pH = -log[H⁺]

• Therefore, [H⁺] = 10^(-pH)

• [H⁺] = 10^(-11.14)

Step 3: Calculate 10^(-11.14).

• This is the inverse log function.

• Scientific calculators have a "10^x" button. Enter -11.14 and then use that function.

• 10^(-11.14) = 7.244 × 10⁻¹² M

Final Answer for #3: The [H⁺] of the solution is 7.24 × 10⁻¹² M (rounded to three significant figures).

Summary of Answers:

1. [H₂O] = 55.56 M

2. pOH = 10.44

3. [H⁺] = 7.24 × 10⁻¹² M

practice questions

the molecular weight of water is 18g/mol and the density of water is 1g/ml

if the pH of solution is 3.0, what is its [OH-]? and what is it [H+]?

Given:

• pH = 3.0

---

1. Find the [H⁺]

The definition of pH is the negative logarithm of the hydrogen ion concentration:
pH = -log[H⁺]

We can rearrange this formula to solve for [H⁺]:
[H⁺] = 10^(-pH)

Calculation:
[H⁺] = 10^(-3.0)
[H⁺] = 1.0 × 10⁻³ M

---

2. Find the [OH⁻]

There are two common ways to find [OH⁻]. We can use the relationship between [H⁺] and [OH⁻] via the ion product of water, K_w.

The Formula:
K_w = [H⁺][OH⁻] = 1.0 × 10⁻¹⁴ (at 25°C)

We can rearrange this to solve for [OH⁻]:
[OH⁻] = K_w / [H⁺]

Calculation:
[OH⁻] = (1.0 × 10⁻¹⁴) / (1.0 × 10⁻³)
[OH⁻] = 1.0 × 10⁻¹¹ M

what is the pH of a solution whose [H+] is 2.75×10^-4 M?

Given:

• [H⁺] = 2.75 × 10⁻⁴ M

Formula:

The pH is defined as the negative logarithm (base 10) of the hydrogen ion concentration:
pH = -log₁₀[H⁺]

Calculation:

1. Take the logarithm (log) of the concentration.

   • log(2.75 × 10⁻⁴) = log(2.75) + log(10⁻⁴)

   • log(2.75) ≈ 0.439

   • log(10⁻⁴) = -4

   • Therefore, log(2.75 × 10⁻⁴) = 0.439 + (-4) = -3.561

2. Take the negative of the result.

   • pH = -(-3.561)

   • pH = 3.561

3. Apply significant figures.

   • The concentration (2.75 × 10⁻⁴) has three significant figures.

   • The digits after the decimal point in a pH value represent the significant figures in the original concentration.

   • Therefore, we round the pH to three significant figures after the decimal point: 3.561

Final Answer:

The pH of the solution is 3.561.

our bodies produce about 22,000 milliequivalents of acid per day through metabolism. if the blood were not buffered, the blood pH would drop to pH 1-2.

strong acids like sulferic acids are rare in the body.

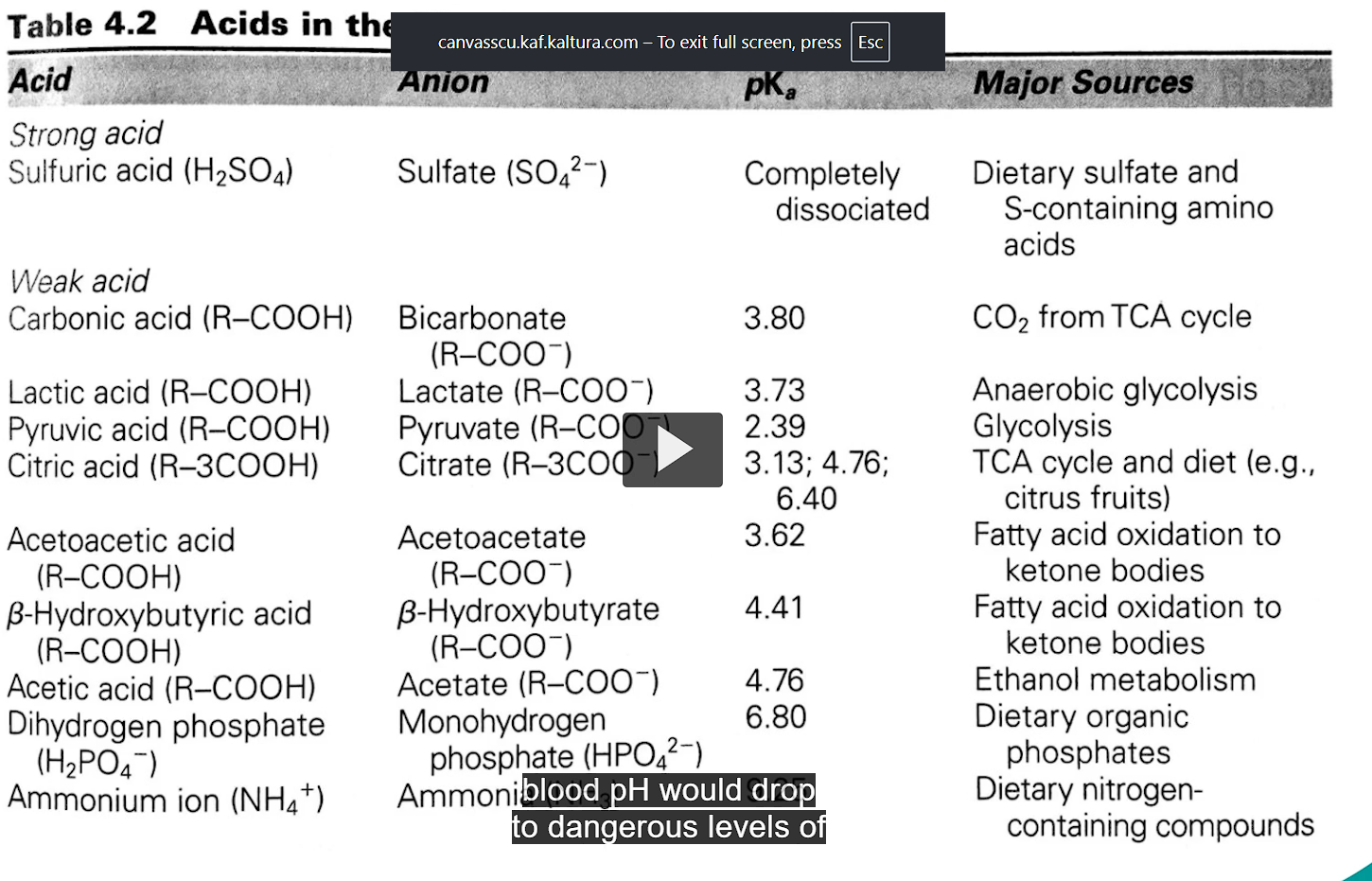
in biology we have mainly weak acids

strong acids completely dissociate, the proton will not be able to get back to the acid.

most biological acids are weak acids

partial dissociation of a weak acid serves as a buffering system.

what is the formula for pKa?

pKa=-LogKa

what do they want you to do with the HH equation?

use pKa or pH to calculate the concentration of the conjugate base, acid, and the proton concentration in the solution.

to survive, blood pH must remain tightly regulated between 7.35 and 7.45

compartmentalization, such as what you see in the stomach and lysosomes, where you have a low pH

excretion, as you see in the kidneys, is when we can eliminate excess protons by producing ammonia

buffering systems such as the bicarbonate system

respiratory compensation by adjusting co2 levels in the lungs.

why are weak acids good buffers?

they partially dissociate as seen in these equations, creating an equilibrium between the acid and the base.

titration (you are adding base to acid)

1. starts at a low pH, acetic acid, fully protonated. zero amount of base is added

2. pH=pKa=4.76. it is as this point that you know the molecule is half concentrated with the proton and half deprotonated. THIS HALF PROTONATED HALF DEPROTONATED ALLOWS FOR A BUFFERING REGION. the buffering region is 1 pH above or below the point at which the pH=pKa.

3. as you move to the right of the x-axis, when 100% of the molecule is titrated, the acid has lost the proton because of the base added (note, you can see the negative charge)

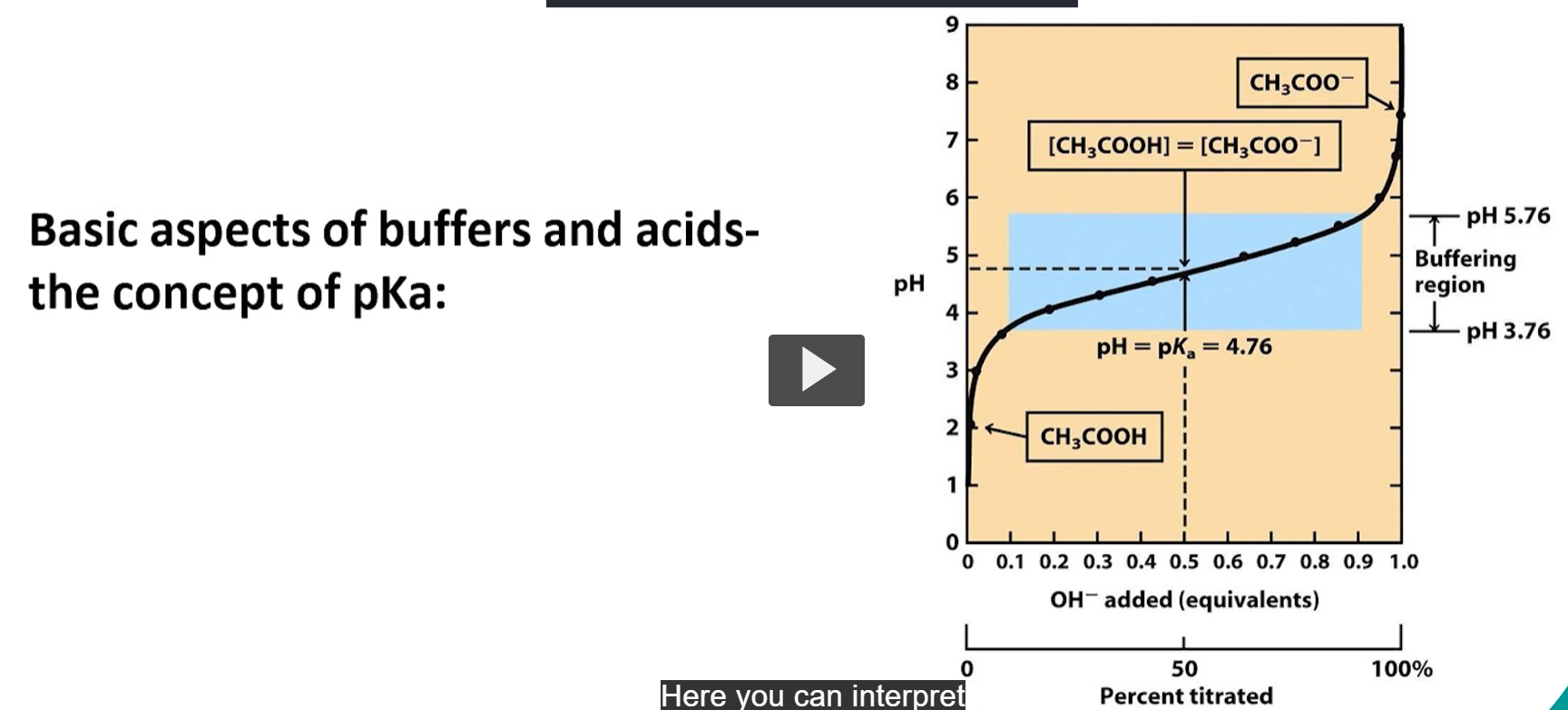
when does the best buffering occur?

when the pKa is close to the pH desired.

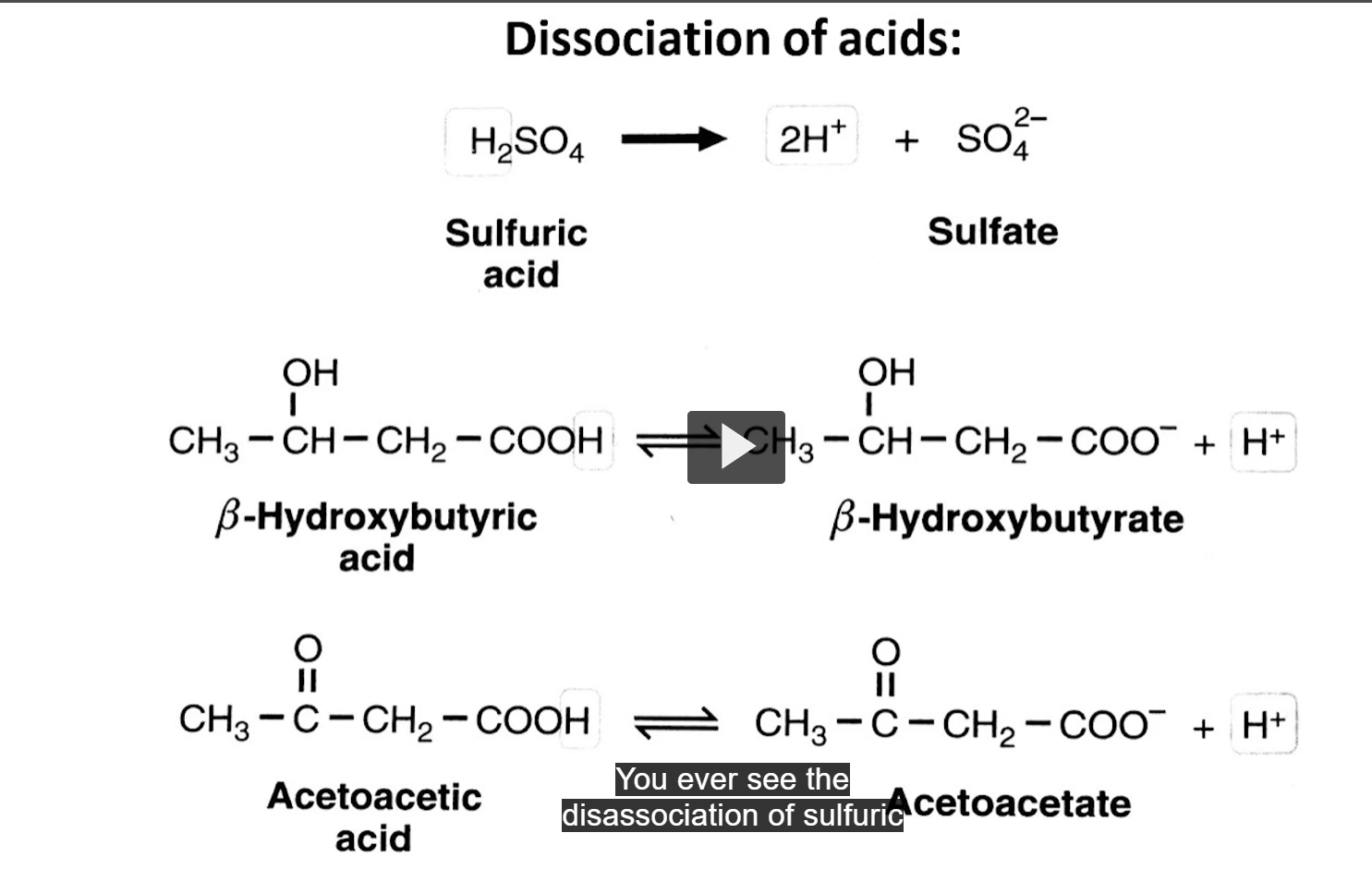
use the arrows to identify which acids are weak and which acids are strong

the acids that are strong have ONE arrow because they dissociate completely

the acids that are weak have EQUILIBRIUM DOUBLE ARROWS, showing back and forth because they don’t dissociate completely, hence why weak acids are able to serve as good buffers

what are the major buffers in the body?

bicarbonate buffer system (for blood)

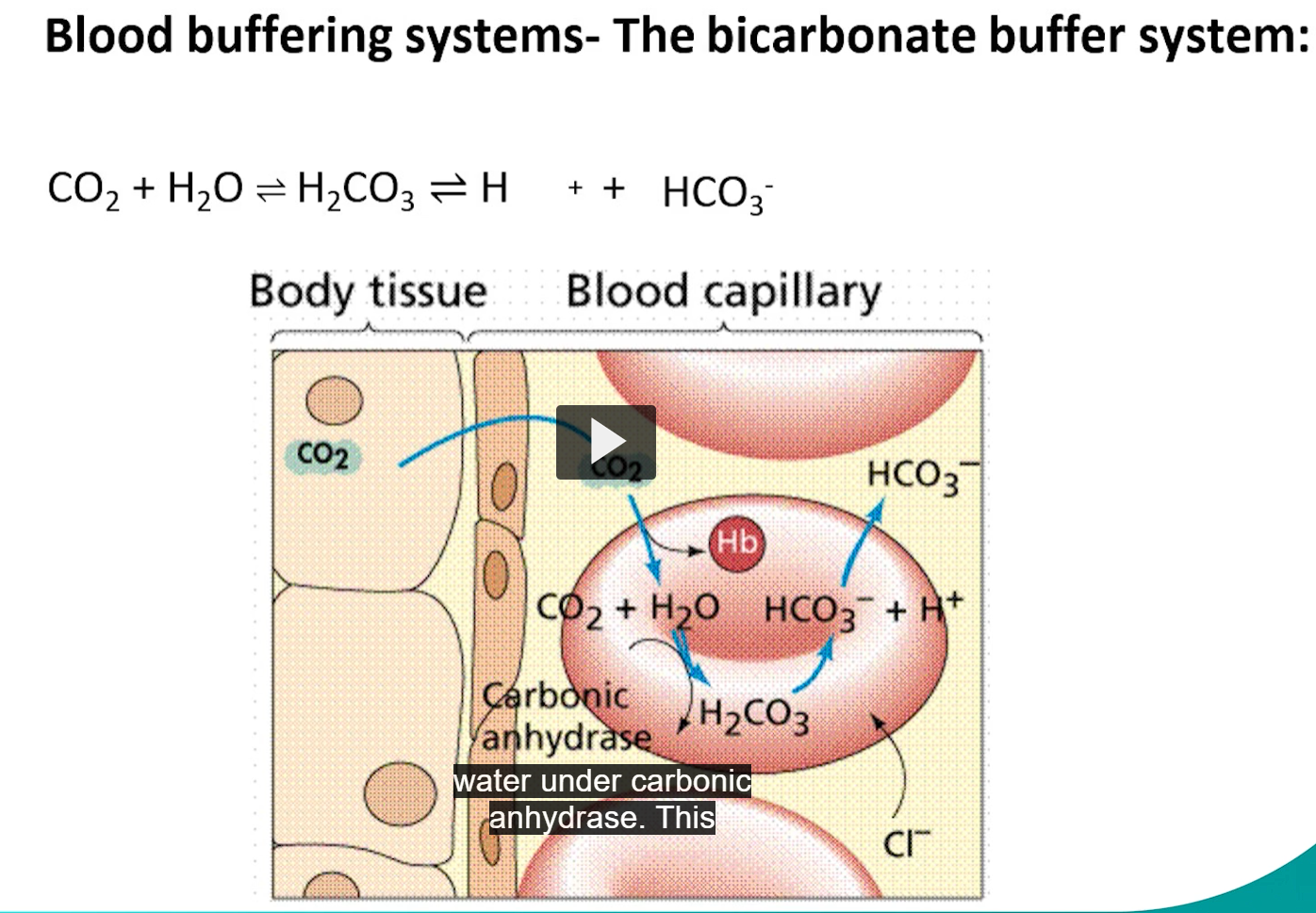
the bicarbonate buffering system is powered by co2, a product of oxidative metabolism, co2 + water = carbonate acid, carbonic acid dissociates at physiological pH to bicarbonate and a proton.

carbonic anhydrase catalyzes both direction

HYPER ventilation drives the reaction to the left, causing the pH to rise.

HYPO ventilation drives the reaction the right, causing the pH to decrease.

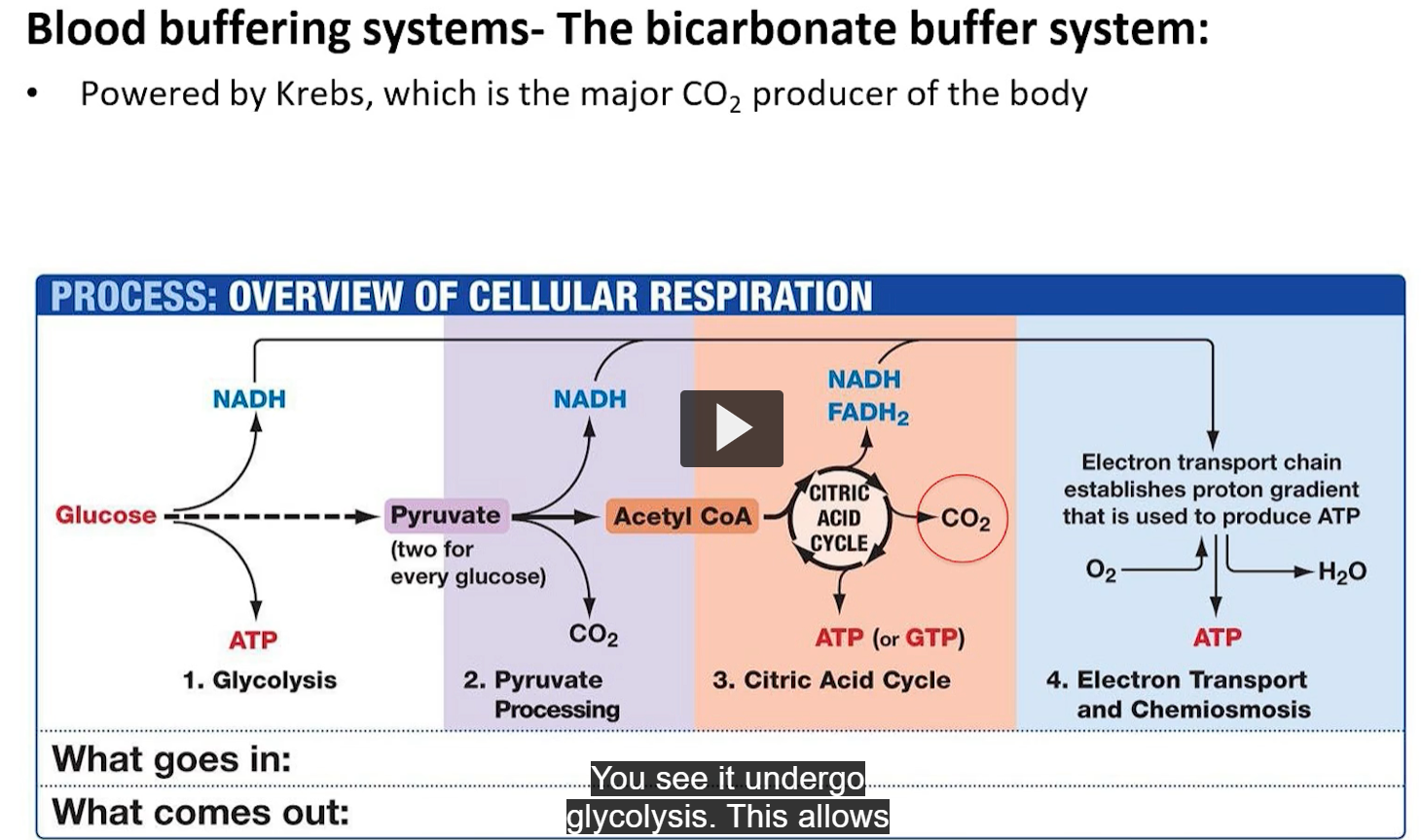
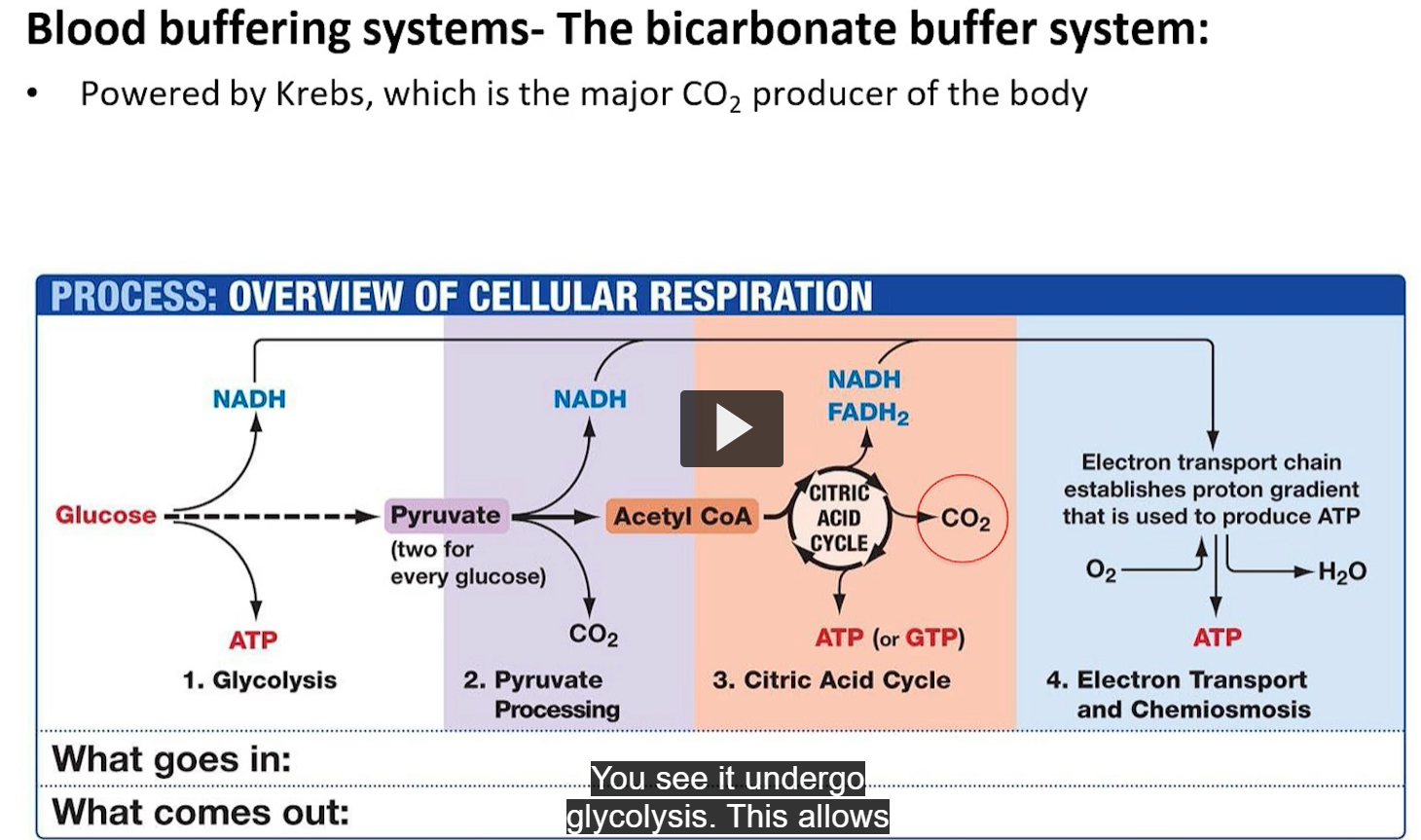
1. glucose comes into the body

2. glucose undergoes glycolysis

3. formation of pyruvate and addition of proton to NAD, and production of ATP.

4. pyruvate gets processed further

5. this ultimately tells you that you are producing a lot of CO2 in the end.

what happens to co2 + water under carbonic anhydrase

co2+ water= carbonic acid

carbonic acid dissociates into a proton and bicarbonate

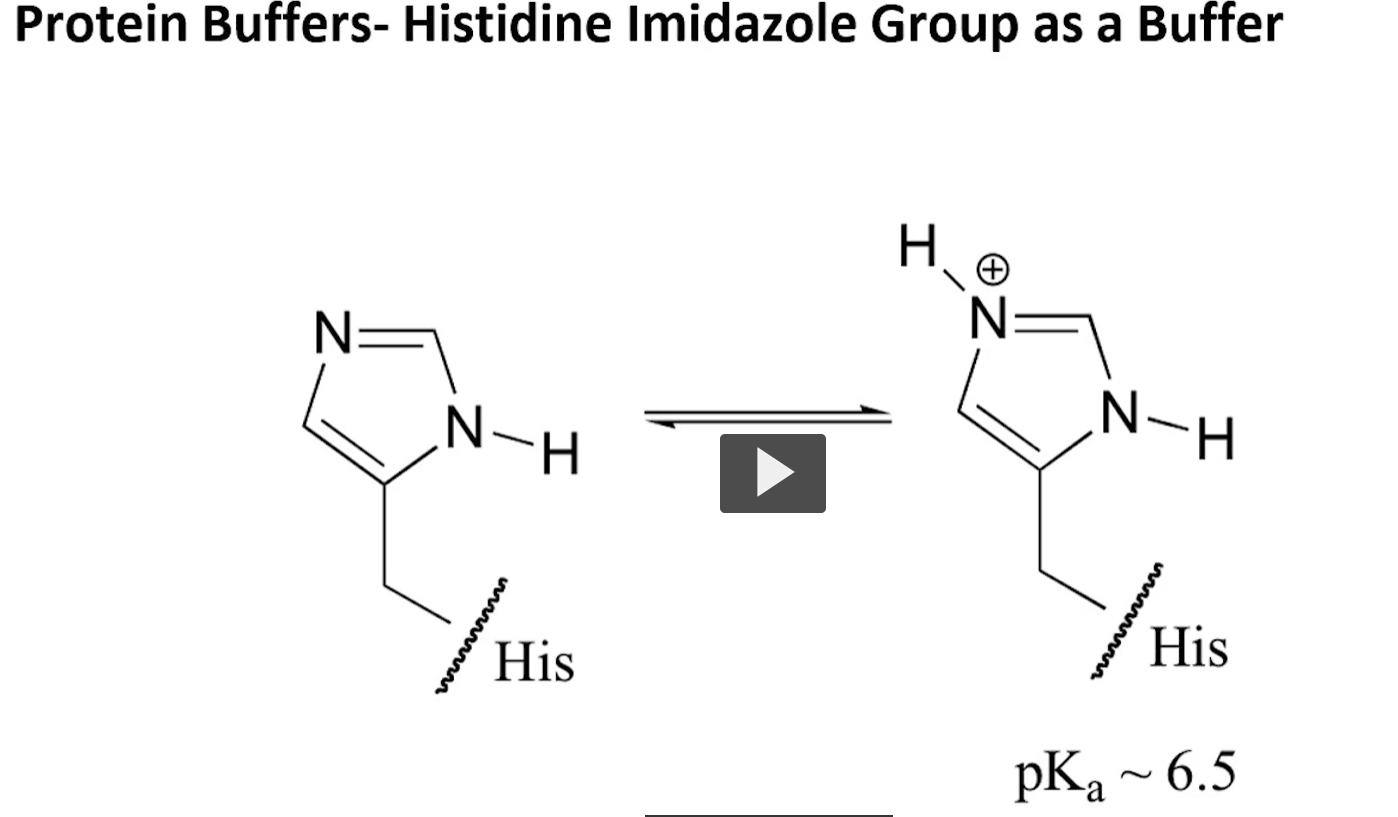
amino acid buffers

histidine!

the TOP LEFT NITROGEN in the imadizole ring is able to take up and proton and drop it off again.

this allows histidine to be a buffer.

lactic acid, a weak organic acid, has a pka of 3.86. during strenous exercise, lactic acid can accumulate in muscle cells to produce fatigue. if the ratio of the conjugate base form of lactate to the conjugate acid form of lactic acid in muscle cells is approximately 100 to 1, what would be in the pH in muscle cells?

A) 1.86

b) 2.86

c) 3.86

d) 4.86

e) 5.85

Step 1: Recall the Henderson-Hasselbalch Equation

The equation for a weak acid is:
pH = pKa + log₁₀([A⁻] / [HA])

Where:

• pH is the value we want to find.

• pKa is given as 3.86.

• [A⁻] is the concentration of the conjugate base (lactate ion).

• [HA] is the concentration of the conjugate acid (lactic acid).

Step 2: Identify the Given Ratio

The problem states the ratio of conjugate base to conjugate acid is 100 to 1.
This means:
[A⁻] / [HA] = 100 / 1 = 100

Step 3: Plug the Values into the Equation

pH = pKa + log₁₀([A⁻] / [HA])
pH = 3.86 + log₁₀(100)

Step 4: Solve the Logarithm

log₁₀(100) = 2
(Because 10² = 100)

Step 5: Calculate the pH

pH = 3.86 + 2
pH = 5.86

Step 6: Match the Answer to the Options

The calculated pH is 5.86. Looking at the options:
e) 5.85

This is a rounding difference. The intended correct answer is clearly e) 5.85.

Final Answer and Explanation

The pH in the muscle cells would be approximately 5.86 (so option E, 5.85, is correct).

Why this makes sense: The pKa (3.86) is the pH where the ratio [A⁻]/[HA] would be 1. Since the ratio is much higher (100:1), the pH must be significantly above the pKa. A pH of 5.86 is exactly 2 units above the pKa of 3.86, which corresponds to a 100-fold excess of the conjugate base, matching the information given in the problem.

homework question

practice problem, metabolic acidosis

here you have an example of metabolic acidosis

here you will be thinking of using the relevant labratory values such as blood pH, bicarbonate and CO2 concentrations to determine or diagnose what is happening to the patient.

you should be able to use the numbers that your provided to be able to calculate the different components of the buffering systems.

EQUATIONS

WATER EQUILIBRIUM

what is the equation for the autoionization of water?

what is the equation for the equilibrium constant (Kw) of water?

what temperature is Kw at?

1. equation for autoionization of water (look in the picture)

2. the equation for the autoionization of water makes the equilibrium constant Kw. At 25C.

what is Kw?

what is the relationship between Kq and temperature?

what is the relationship with pure water?

Kw is the ion product constant for water, the PRODUCT (result of two numbers multiplied) of the acid and base concentrations at equilibrium.

Kw​=[H⁺]×[OH^-]=1.0×10^-14

in temperature, you need to compare the temperature to 25C. at 25C, Kw= 1.0×10^-14. At 35C, the equilibrium shifts to the right and more H+ and OH- are produced because of the equation. at higher temperature, the reaction shifts to the right.

In pure water, the only source of H⁺ and OH⁻ is the autoionization reaction itself.

• The reaction must create equal amounts of H⁺ and OH⁻.

what is pH?

what is pOH?

what is pKw?

what is pH+ pOH?

why do we use -log, and what does the p notation mean?

what do we do to go backwards from pX to concentration?

The negative log of the hydrogen ion concentration. pH=-log[H+]

pH=7

The negative log of the hydroxide ion concentration. pOH=-log[OH-]

pOH=7

The negative log of the water dissociation constant. pKw=-log[Kw]

pKw=14

To simplify working with these very small numbers, we use logarithms. This is where the "p" notation comes from. p means -log₁₀.

to go backwards from pX to concentration, [H+]=10^-pH
[OH−]=10^-pOH

Ka and pKa?

what is the formula for Ka?

Ka: the strength of an acid

pKa: the negative log of the strenght of an acid

Ka= [proton concentration] [base conc]/[acid conc]

higher Ka means a stronger acid, lower Ka means a weaker acid

lower pKa means a stronger acid, higher pKa means a weaker acid.

practice question: find H+ from pH, pH=4.6

1. the formula for pH= -log[H+]

2. [H+]=10^-4.6, because 10 cancels log, and because the log is negative, we make the exponent negative

find pH from H+, [H+]=1.8×10^-3

note that [H+] will be an exponent, while pH will not be an exponent

1. Finding pH from [H⁺]: If $[\ce{H+}] = 1.8 \times 10^{-3}$ M, then pH = -log(1.8 × 10⁻³) = 2.74

you can use the exact same way from the other flashcards to find OH- and pOH, you just need to know that

1. pOH=log[OH-]

2. [OH-]=log^pOH

how to find pH from pOH

1. pH+pOH= 14

you see? by taking the -log, you make the numbers bigger and easier to work with.

1. Finding pOH: If pH = 2.74, then pOH = 14.00 - 2.74 = 11.26

compare the strength of an acid using pKa

1. Comparing Acid Strength: Acid X has pK_a = 5.0. Acid Y has pK_a = 3.0. Acid Y is the stronger acid because it has a lower pK_a.

making a buffer

1. Making a Buffer: To make a buffer at pH = 5.0, choose an acid with a pK_a close to 5.0 (e.g., acetic acid, pK_a = 4.76). Then use the Henderson-Hasselbalch equation to find the required ratio of [A⁻]/[HA].

what is the difference between pKa and pK’?

pKa (a for perfect) is the ideal, theoretical measure of an acid's strength

pK' (not perfect) is the practical, real-world measure taken under controlled, specific lab conditions to account for environmental factors.