week 5 - k means algorithm

recall

Partitional clustering problem can be framed as the following optimisation problem:

k-means

= iterative, greedy descent algorithm - aims to find sub-optimal solution to optimisation problem in (1)

k-means iteratively alternates between the following 2 steps:

• Assignment step: for a given set of k cluster centroids, k-means assigns each example to the cluster with closest centroid

  • (see pic) = equivalent to fixing the centroids + optimising the cluster assignment to ensure low wcss

• Refitting step: re-evaluate + update the cluster centroids

  • = equivalent to fixing the cluster assignment + optimising the centroids to ensure low wcss

  • consequently, over iterations, wcss continues to decrease

the algorithm: k means algorithm

input: no of k clusters + N examples (x⁽¹⁾,…x^(N))

1. select k of the N examples at random as centroids + label is as C₁, …, C_K

2. repeat until the cluster centroids don’t change:

   • (assignment step) form k clusters by assigning each observation to its closest centroid, i.e. (see pic)

   • (Refitting step) compute the centroid of the obtained k clusters as ( see pic)

points to note

• initial choice of cluster centroids are randomly chosen from the data examples

• however, centroids found by k-means over the iterations need not be data examples

• cluster assignment = based on squared Euclidean distance

• stopping criterion: stop when cluster centroids don’t change

illustration

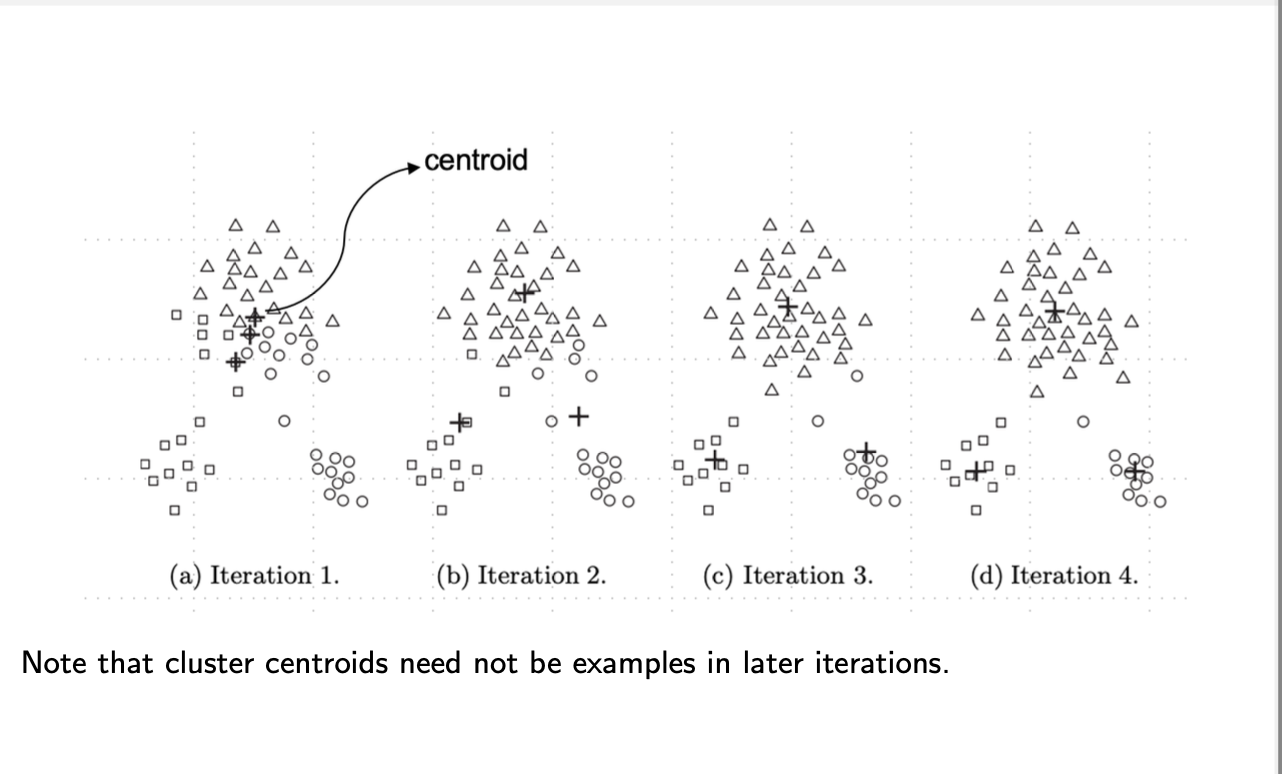
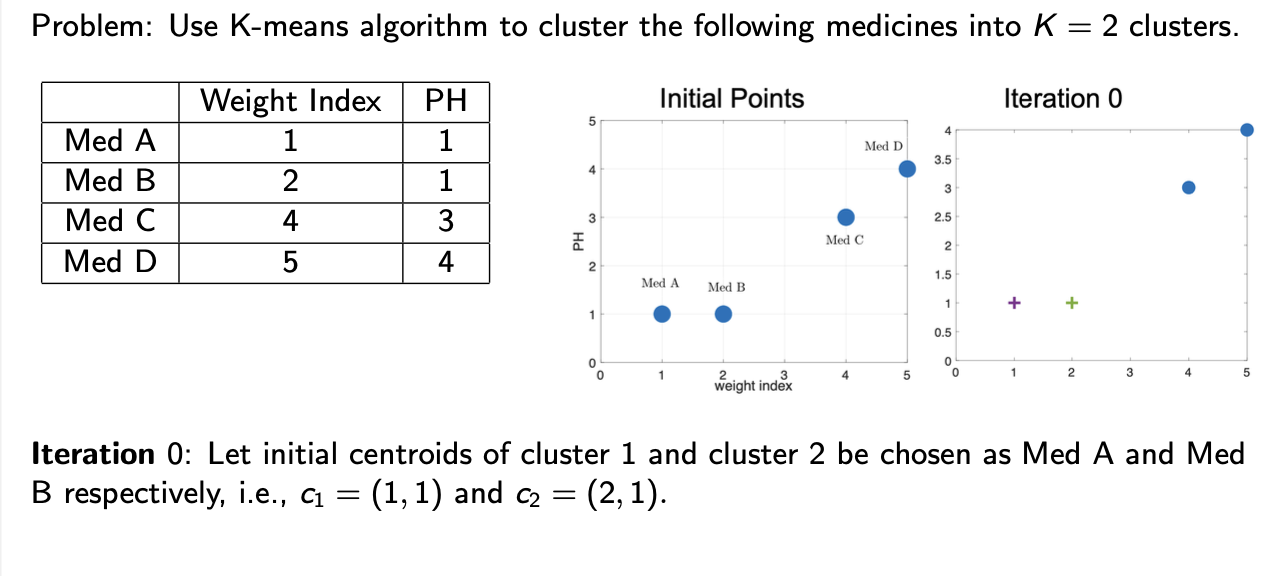
example 1: clustering of medicines

problem : use k-means algorithm to cluster the following medicine into k=2 clusters

iteration 0: let initial centred of cluster 1 and cluster 2 be chosen as Med A and Med B respectively e.g. C₁=(1,1) and C₂=(2,1)

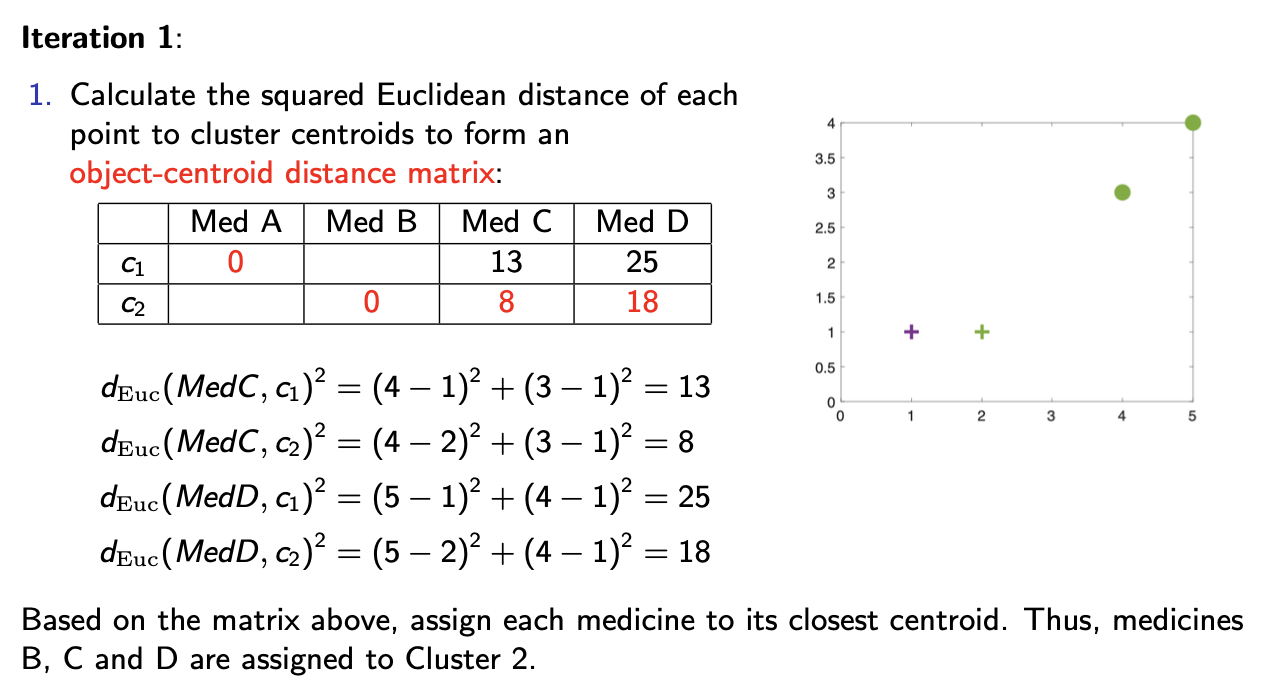
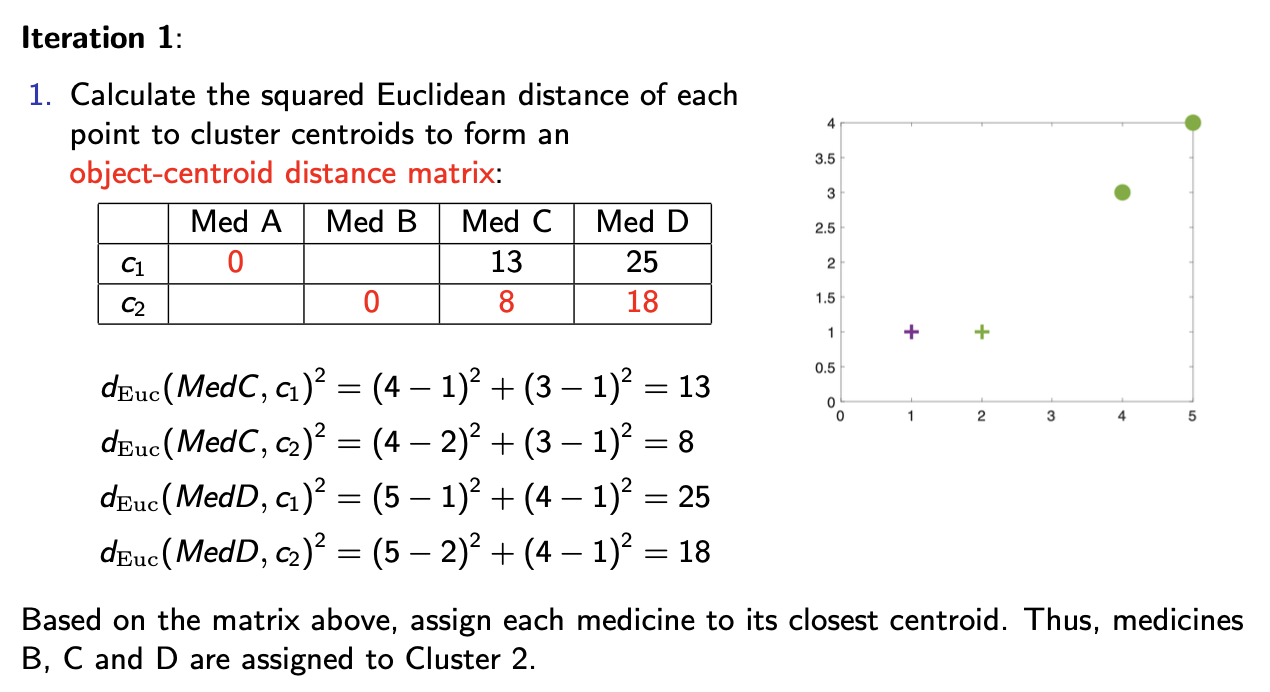
iteration 1:

1. calculate the squared euclidean distance of each point to closer centroids to form an object-distance matrix

   • based on the matrix, assign each medicine to its closest centroid. Thus, medicines B, C and D are assigned to cluster 2

continued

Iteration 1 cont:

2. update the centroids of the clusters obtained in the previous step → results in: (see pic) - green + symbol

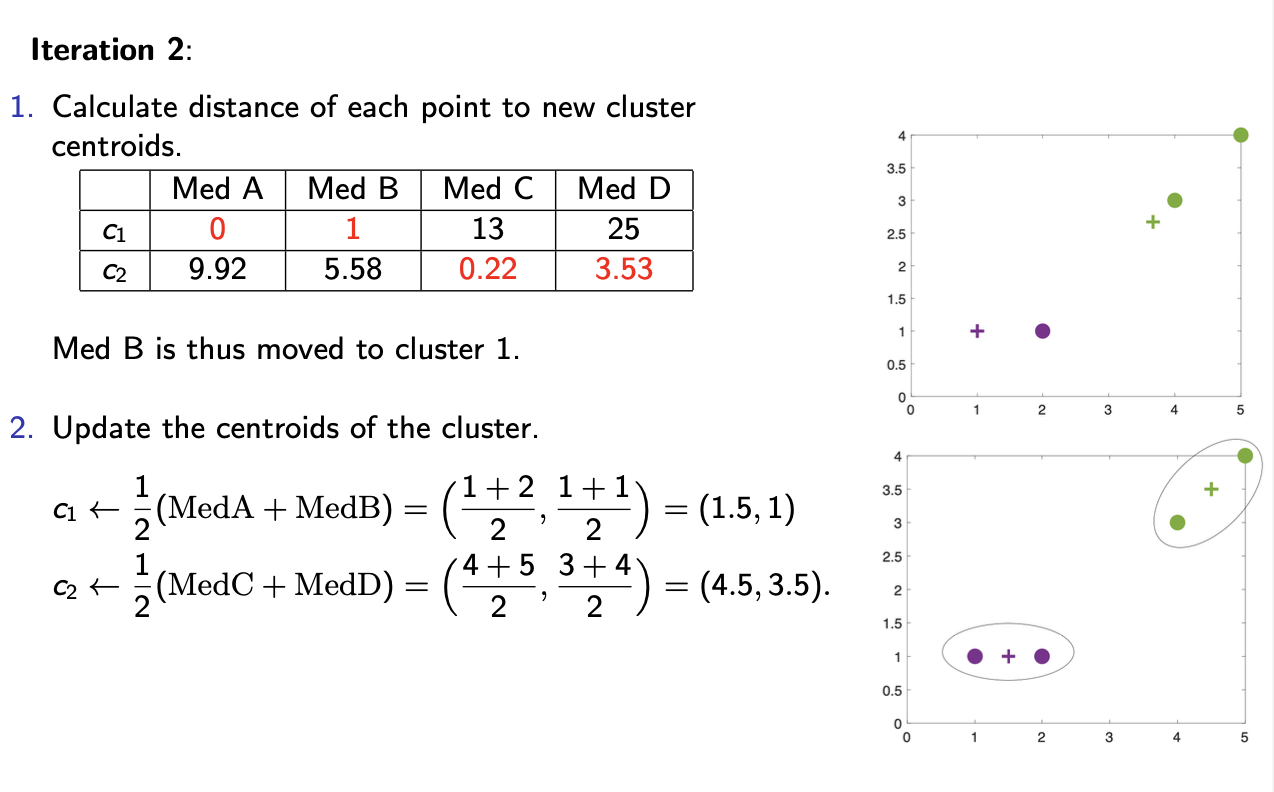
iteration 2:

1. calculate distance of each point to new cluster centroids → med B is thus moved to cluster 1 - as only 1 away from cluster 1 and 5.58 away from cluster 2

2. update the centroids of the cluster

iteration 3:

• repeat the same steps as before

• note that the cluster assignments don’t change

• algorithm has converged

  • converged = reached a steady/stable state - further iterations are unlikely to significantly change the result

space + time complexity of k-means

- space requirement = modest → only data observations + centroids are stored

- storage complexity = of order O((N+k)m) where m = no.of feature attributes

- time complexity of k-means = of order O(IKm) where I=no. iterations required for convergence

- importantly, time complexity of k-means is linear in N

• space complexity = amount of memory required by an algorithm to solve a problem →function of the input size

• storage complexity = amount of memory to store the input data itself as well as additional memory used by the algorithm

challenges + issues in k-means

• does the k-means algorithm always converge?

• can it always find optimal clustering?

• how should we initialise the algorithm?

• how should we choose the no. of clusters?

convergence of k-means

• zt each iteration, the assignment + refitting steps ensure that the wcss in (1) monotically decreases

• moreover , k-means work with infinite number (k^N) of partitions of the data

  • above 2 conditions ensure that the k-means algorithm always converges

BUT → optimisation problem of (1) is non-convex

• as such, k-means algorithm may not converge to the global minimum, but to a local minimum !!!!

  • solution: escaping local minima: multiple random restarts + choose the clustering with lowest wcss

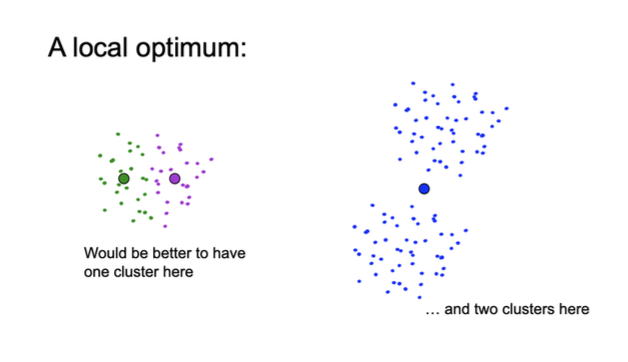
choice of initial cluster centroids

choosing initial cluster centroids is crucial for k-means algorithm

• diff initialisations may lead to convergence to diff local optima

• k-means is a non-deterministic algorithm : where the outcome is x entirely predictable based solely on the input + the algorithms logic - can produce diff results for the sae input under diff executions

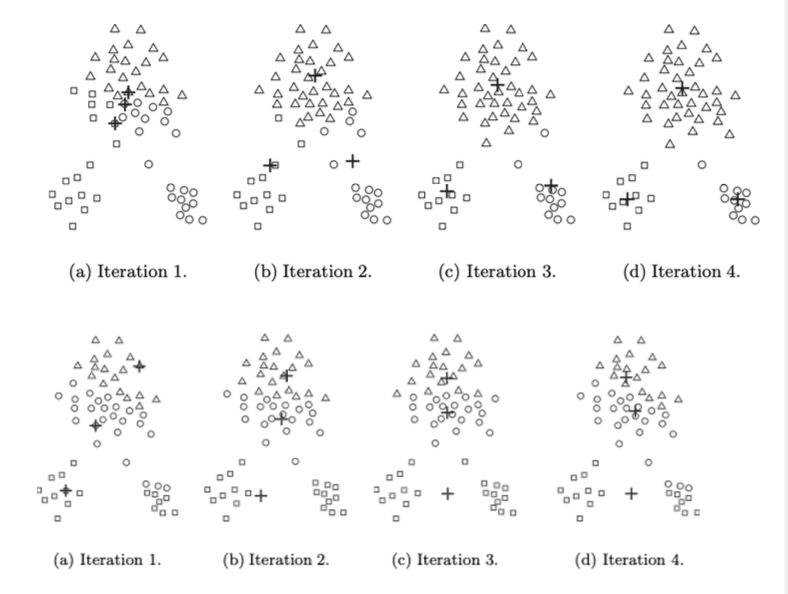
solutions

• run multiple k-means algorithm starting from randomly chosen cluster centroids - choose the cluster assignment that has the minimum wcss

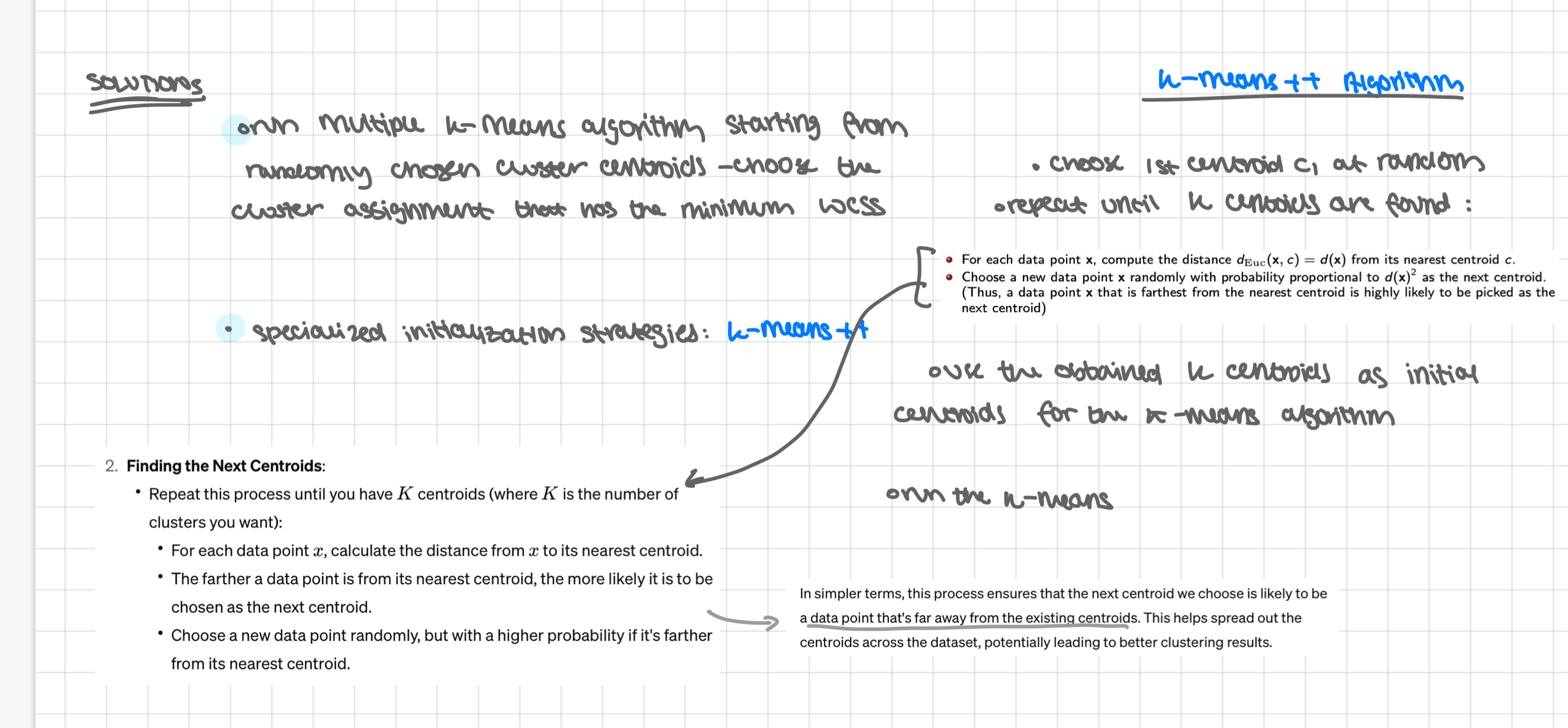
• specialised initialisation strategies : k-means++

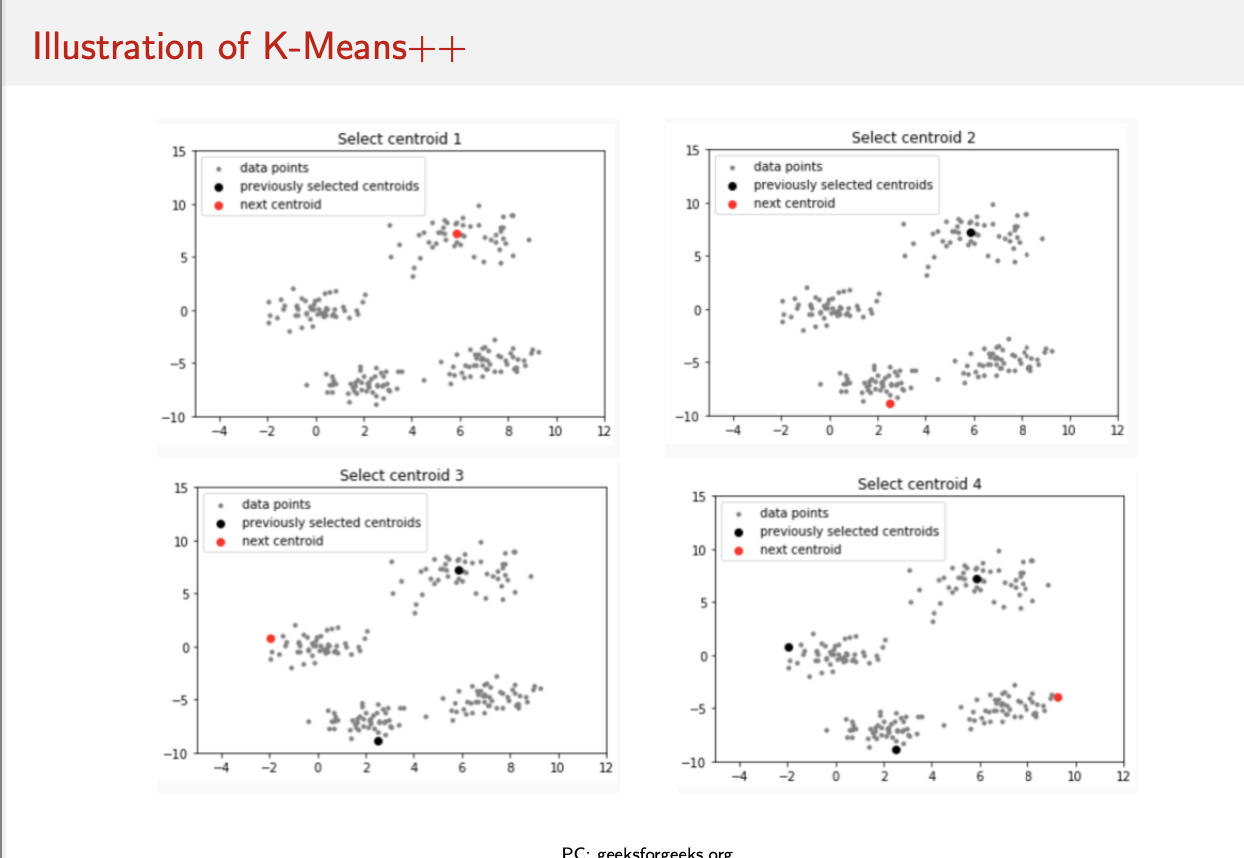
k-means++

• choose 1st centroid C₁ at random

• repeat until k centroids found:

  • For each data point x, compute the distance d_Euc(x, c) = d(x) from its nearest centroid c.

  • Choose a new data point x randomly with probability proportional to d(x)² as the next centroid.

    (Thus, a data point x that is farthest from the nearest centroid is highly likely to be picked as the next centroid)

• use the obtained k-centroids as initial centroids for k-means algorithm,

• run the k-means

choice of the number of k clusters

conventional approach: use prior domain knowledge

• example: data segmentation - a company determines the no. of clusters into which its employees must be segmented

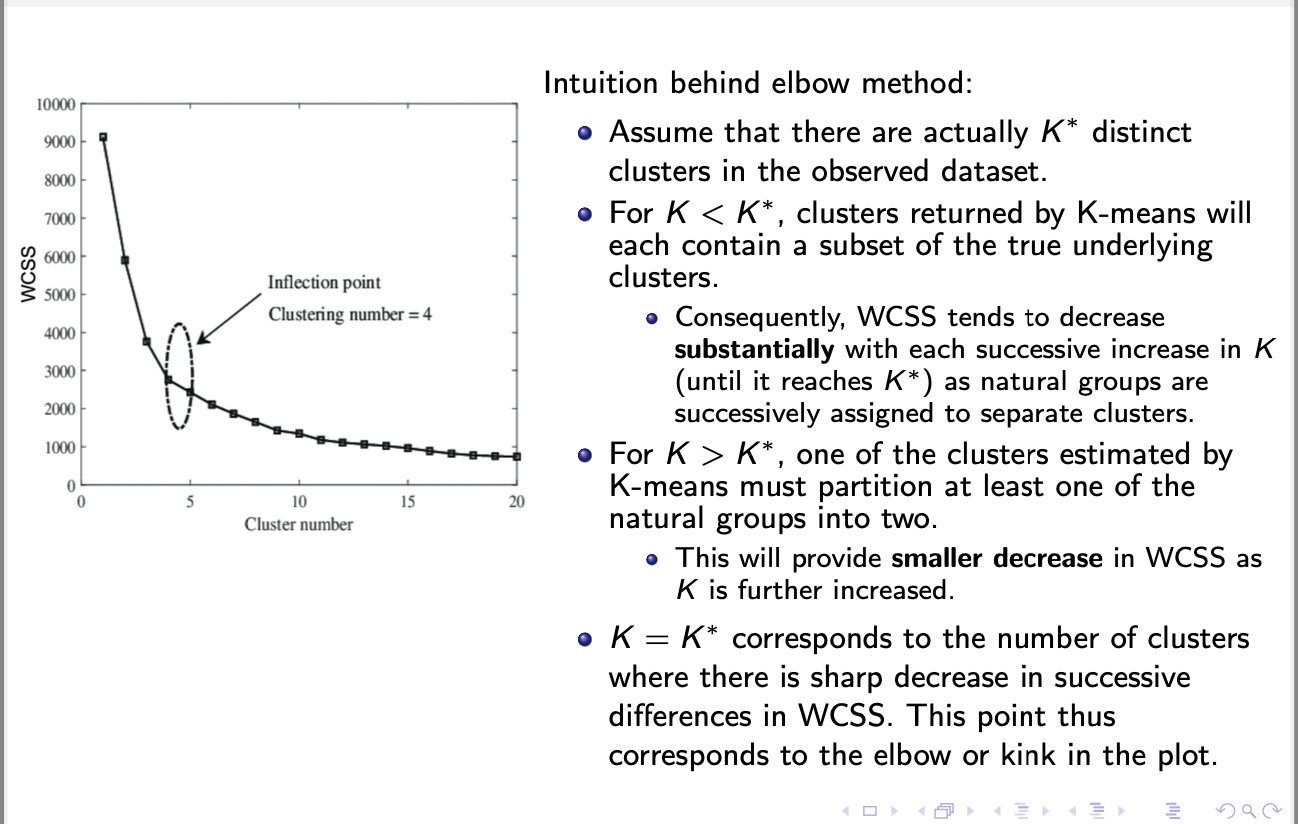
a data-baed approach for estimating the number of natural clusters in the data set: elbow method

elbow method

• run k-means algorithm repeatedly for increasing values of k

• evaluate the wcss of the obtained clustering structure in each run of k-means

• plot wcss(c) as a function of the number k of clusters

• optimal k lies at the elbow of the plot

drawbacks of elbow method:

• heuristic concept

• not easy to identify the elbow

elbow method

when k<the no. of distinct clusters (K*) adding more clusters = substantial decrease in wcss- each cluster will capture a subset of the true clusters = making them tighter + ↓ wcss

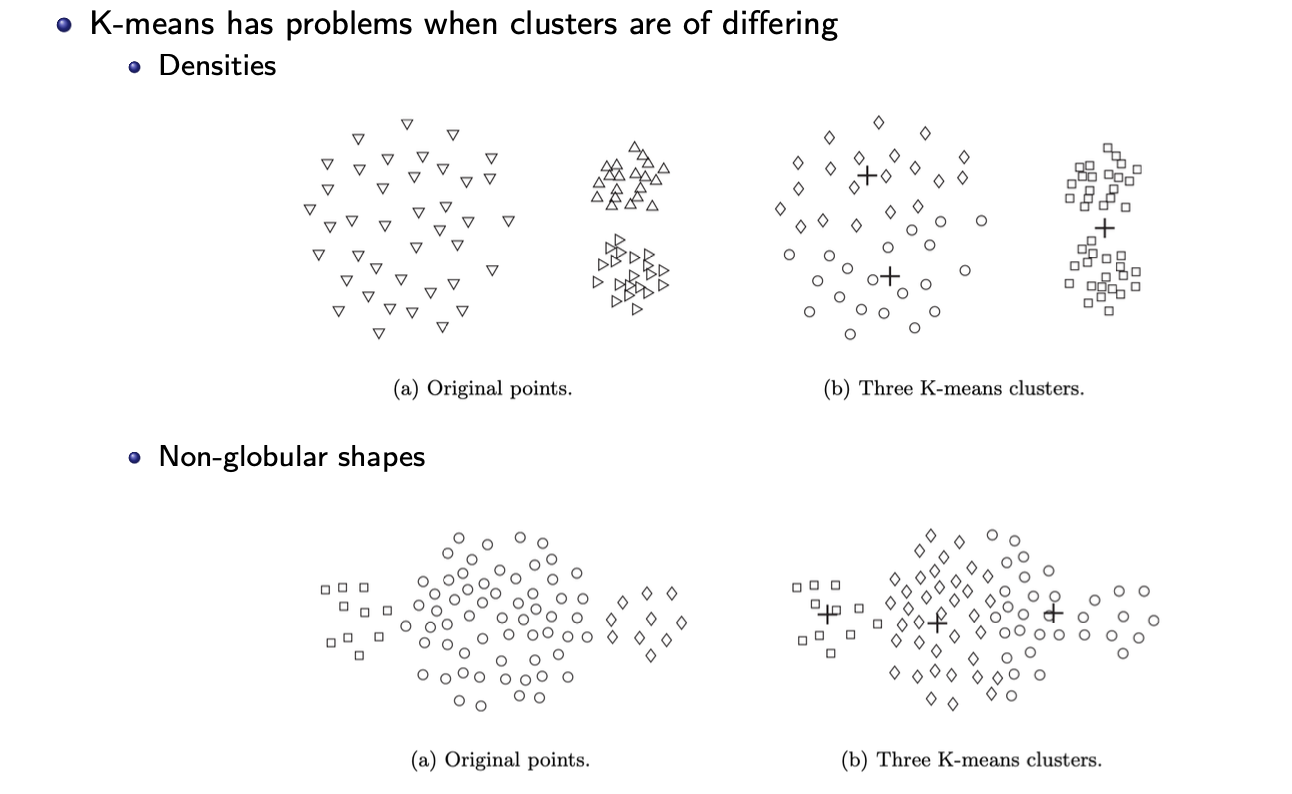
other limitations of k-means

problems when. outliers are present - can influence the clusters that are found + also ↑ the wcss

k-means has problems when clusters are of differing:

• sizes

• densities

• non-globular shapes

one solution = to find a large no. of clusters such that each of them represents a part of a natural cluster. But thwse small clusters need to be put together in a post processing step

application of k-means

• k-means algorithm is a key tool in the area of image + signal compression - particularly in vector quantisation

vector quantisation via k-means

• break left image into small blocks of 2×2

• results in 512×512 blocks for 4 numbers each regarded as a (feature) vector in ℝ⁴

• run k-means algorithm in the resulting space of feature vectors - clustering process called encoding step in VQ + the collection of centroids is called the codebook

• centre image uses k=200 while right image uses k=4

to represent the compressed image, approximate each of the 512×512 blocks by its closest cluster centroid, known as codeword. Then, construct the image from the centroids, a process called decoding .

storage requirements:

• for each block, the identity of the cluster centroid needs to be stored

• this requires log₂(k) bits per block, which equals log₂(k)/4 bits per pixel