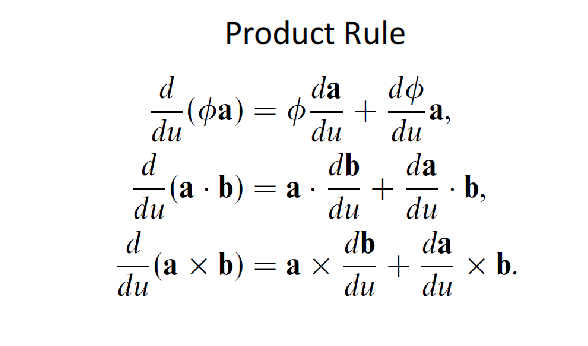Math Vectors

Types Of Vectors

• Position Vectors = A position vector gives the position of a point relative to a fixed point (usually the origin)

• Line Vector = A line vector can “slide” along its line of action (e.g. force acting on a body)

• Free Vector = A free vector is completely defined by its magnitude and direction (e.g. velocity)

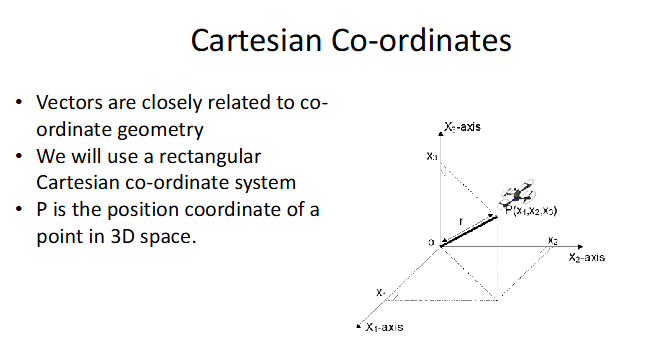
Cartesian Co-ordinates Axes

• P is the position co-ordinate of a point in 3D space

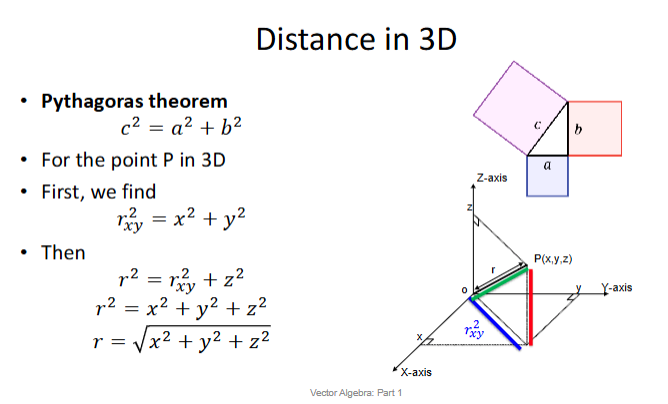
Distance In 3D Space

Pythagoras Theorem

Geometric / Coordinate-Free Representation Of A Vector

• Length indicates magnitude

• Orientation indicates direction of the vector

• Starting point is irrelevant

Equal And Parallel Vectors

• Two vectors a and b are equal if they have the same magnitude and direction i.e. a = b

• Anti-parallel vectors are equal in magnitude but opposite in direction.

Top picture from current lectures

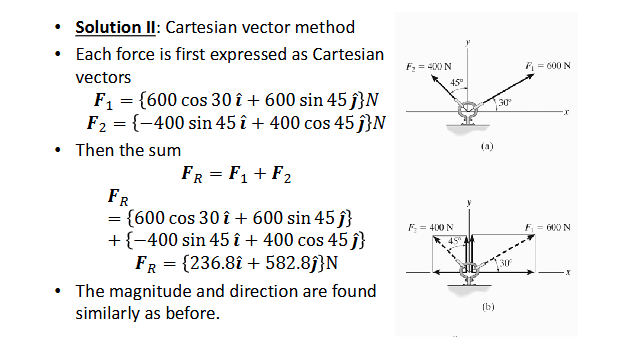
Determine Direction And Magnitude

Example : The link in the figure is subjected to two forces F1 and F2. Determine the direction and magnitude of the resultant force.

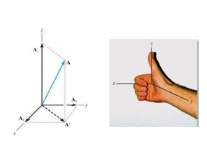
Right Hand Rule

A convention used to determine the direction of a vector resulting from a cross product, indicating how to align the fingers of your right hand with two vectors.

• Goes the direction of the fingers given the thumb is pointing in the direction of the resulting vector.

Unit Vector

A unit vector has a magnitude (modulus) equal to 1. It is defined by:

The Modulus (Magnitude) Of A 3D Vector

Directional Ratios

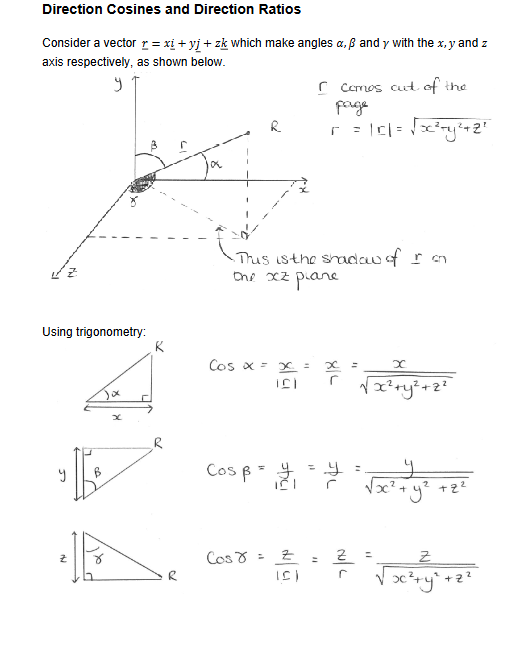
Consider a vector 𝑟 = 𝑥𝑖 + 𝑦𝑗 + 𝑧𝑘 which make angles 𝛼, 𝛽 and 𝛾 with the 𝑥, 𝑦 and 𝑧 axis respectively, as shown below

The values of
𝑥/|𝑟|, 𝑦/|𝑟| and 𝑧/|𝑟|
are called the direction cosines of vector 𝑟 = 𝑥𝑖 + 𝑦𝑗 + 𝑧𝑘. These allow the direction of the vector with respect to the axes to be determined.
The ratios 𝑥: 𝑦: 𝑧 are called the direction ratios of the vector.

Directional Ratios Continued

l, m, n are the direction cosines of the line OP

m = cos (extended b sign) = (y / r)

n = cos (upsidedown fish) = (z / r)

l = cos (a with extra line at top right) = (x / r)

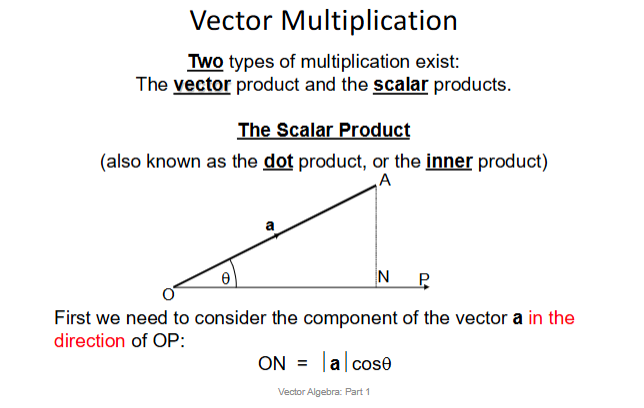
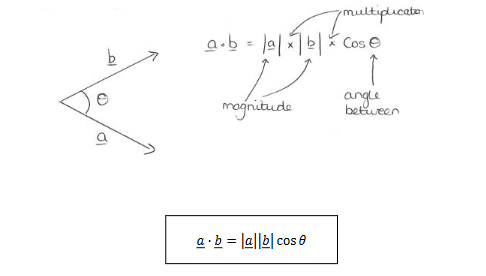
Scalar Product

The scalar product (or ‘dot’ product) of two vectors 𝑎 and 𝑏 is defined as the product of their magnitudes multiplied by the angle between them.

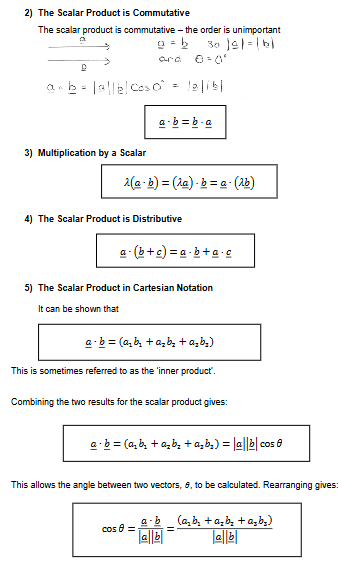
Scalar Product Continued

• If two vectors are perpendicular the scalar product is equal to zero

Vector Product

Top picture is more for this course

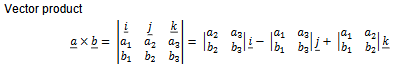
Vector Equation Of A Line

• When one point and a parallel vector is known

Vector Equation Of A Line

• When two points on the line are known

Showing A Point Lies On A Line

Finding Angles Between Two Lines

Two lines L1 and L2

Vector Equation

Can be expressed using a point and two direction vectors that span the plane.

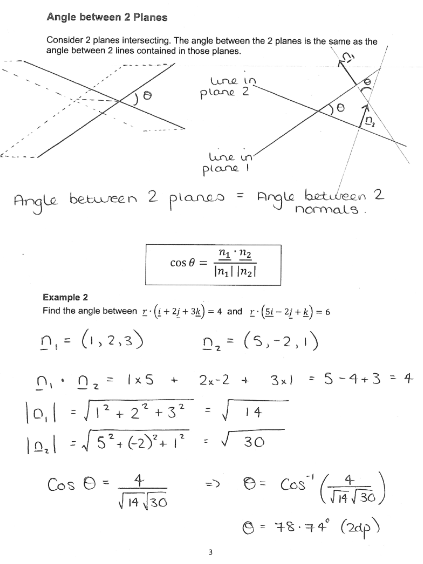
Angle Between Two Planes

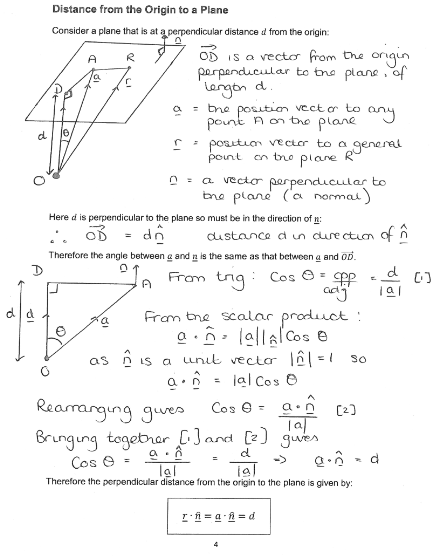
Distance From Origin To A Plane

The shortest distance from a point in space to the plane, calculated using the normal vector of the plane.

Cartesian Equation Of A Plane

An equation representing a plane in three-dimensional space, typically expressed in the form Ax + By + Cz + D = 0, where A, B, and C are the coordinates of the normal vector to the plane.

Relationship Between Work Done And Dot Product

• Definition of work = Amount of displacement along the direction of displacement multiplied by the distance moved

• Work Done = Force x Distance

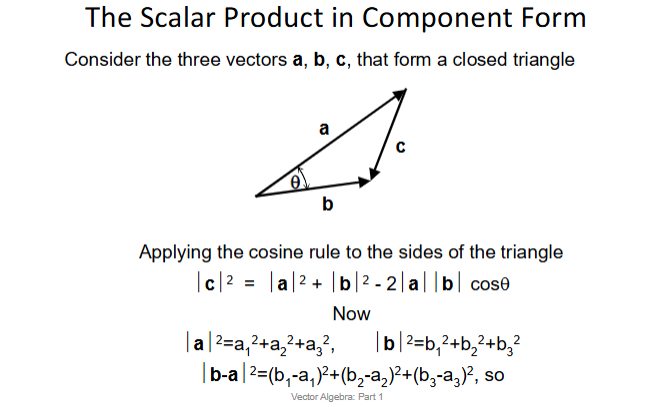
Scalar Product In Component Form

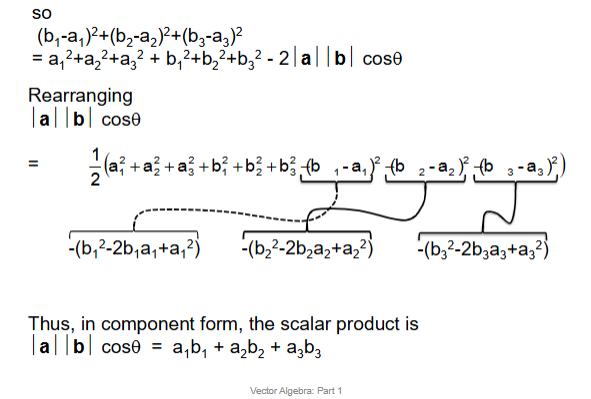
Scalar Product Definition

• You cannot have a scalar product of three vectors. ‘dotting’ the first two gives a scalar.

Scalar Product Using Cartesian Vectors

Powers Of Vectors

Only powers of two can be used in vectors any higher is not possible

Perpendicular Vectors : Scalar Product

• a . b = 0 does not imply that a and b are perpendicular, a could be 0 or b could be zero, its only when a and b are non-zero then a and b are perpendicular

The Moment Of A Force

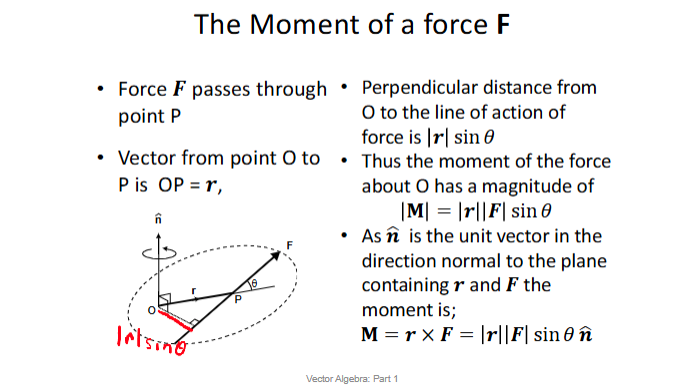
The Moment Of A Force Continued

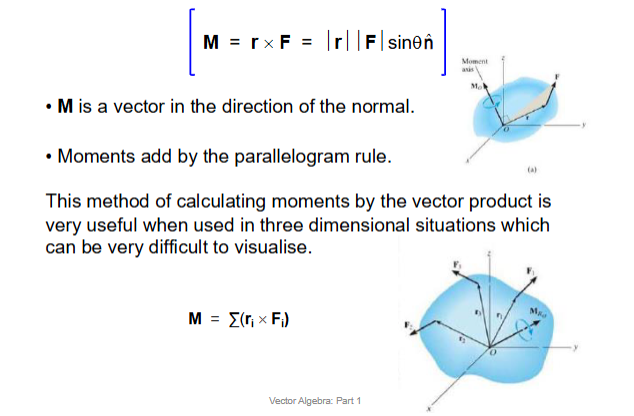
Principle Of Transmissibility

• We can use any position vector r measured from point O to any point on the line of action of the force F. Thus, Mo = r1 x F = r2 x F = r3 x F

• Since F can be applied at any point along its line of action and still create this same moment about point O, then F can be considered a sliding vector. This property is called the principle of transmissibility of a force

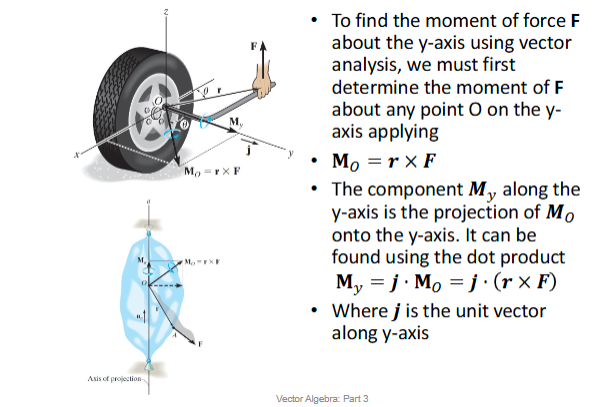
Find Moment Of Force About Y-Axis

• To find the moment of force F about the y-axis using vector analysis, we must first determine the moment of F about any point O on the y-axis applying

• Mo = r x F

• The component My along the y-axis is the projection of Mo onto the y-axis. It can be found using the dot product My = j . Mo = j . (r x F)

• Where j is the unit vector along y-axis

• We can generalise the approach to any axis with unit vector Ua

• Then the moment about an axis is Ma = Ua . Mo = Ua . (r x F)

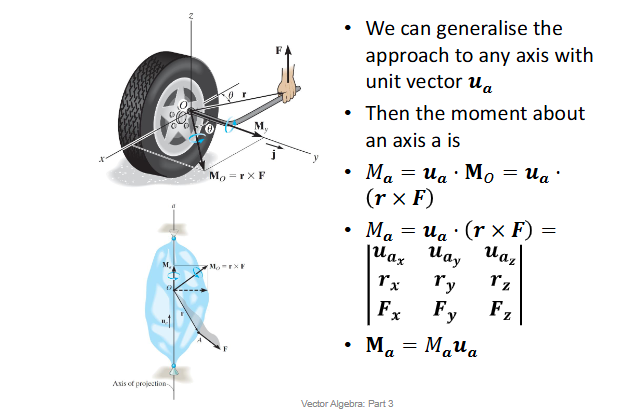
Key Points About Moment About An Axis

• The moment of a force about a specified axis can be determined provided the perpendicular distance da from the force line of action to the axis can be determined. Ma = Fda.

• If vector analysis is used, Ma = Ua . (r x F), where Ua defines the direction of the axis and r is extended from any point on the axis to any point on the line of action of the force.

• If Ma is calculated as a negative scalar, then the sense of direction of Ma is opposite to Ua

• The moment Ma expressed as a cartesian vector is determined from Ma = MaUa

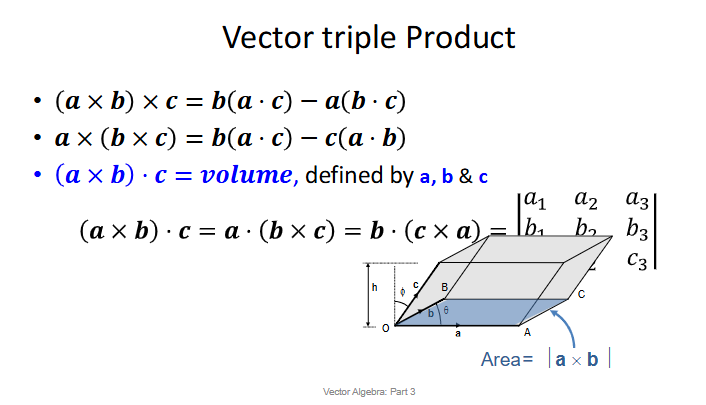
Vector Triple Product

Cartesian Form Vector Product

Cartesian Form Vector Product Continued

Parallel Vectors : Using Cross Product

Two vectors are parallel if their cross product equals zero, indicating they point in the same or opposite directions.

Vector Equation Of A Plane

a = position vector to a point on the plane, called A

r = position vector to a general point on the plane, R

n = a vector perpendicular to the plane (a normal)

Vector Calculus

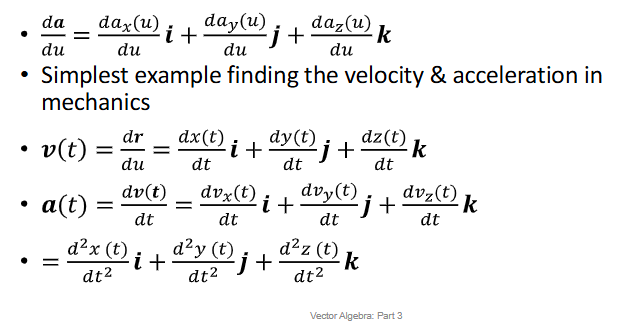
Vector Calculus Product Rule