Chapter 9: Linear Momentum & Collisions

Linear Momentum of a Part

• p = mv

  • m = mass of particle (kg)

  • v = velocity of particle (m/s)

  • vector quantity: direction of the momentum is the same as velocity’s

    • depends on direction & magnitude

A particle with a high p, or linear momentum, is…

• difficult to stop

• large mass with high speed

Net Force of a particle

• F_net = Δp/Δt

• The net force acting on a particle/object is equal to the rate of change of its momentum over time.

• A greater net force will cause a greater change in momentum; net force changes momentum

• Connected to Newton’s 2nd Law: F = ma

Force is equal to a…

change in momentum

A 0.12-kg ball is moving at 6 m/s when it is hit by a bat, causing it to reverse direction and have a speed of 14 m/s. What is the change in the magnitude of the momentum of the ball?

• m = 0.12 kg

• v_i = 6 m/s

• v_f = -14 m/s

• change in magnitude = |Δp| = p_f - p_i = mv_f - mv_i = 0.12 kg(6 - (-14)) = 2.4 kg*m/s

Impulse

• changes momentum

• J = Δp = F_netΔt

  • net force produces impulse

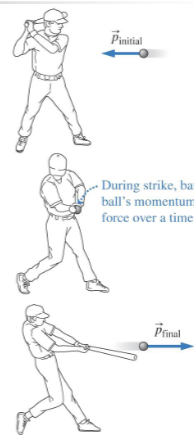
Explain what is happening.

• Impulse occurs when a net force acts over a period of time, resulting in a change in momentum. In this context, the ball undergoes a significant momentum change due to the impact from the bat.

• Bat changes ball’s momentum by exerting a force over a time interval. Strike reverses ball’s momentum.

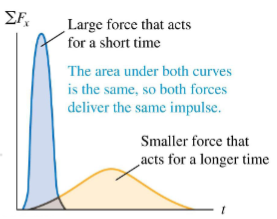
A moderate force will break an egg. However, an egg dropped on the road usually breaks, while one dropped on the grass usually doesn’t break. This is because for the egg dropped on the grass…

a. the change in momentum is greater

b. the change in momentum is less

c. the time interval for stopping is greater

d. the time interval for stopping is less

c. the time interval for stopping is greater

• FΔt = Δp

• Egg m = 1 kg, v = 10

• Grass: t = 5, concrete: t = 1

• Force is 5x greater for egg on concrete

• change in momentum - same: egg goes from moving → stopped

• grass stops egg more slowly & spreads force off

Conservation of Momentum

• when no external forces act on a system consisting of 2 objects that collide with each other, the total momentum of the system remains constant in time

• total momentum before collision = total momentum after collision

• can be generalized to any number of objects

  • applies to the system (inelastic or elastic as long as no outside force)

• p_i = p_f

• m₁v_1i + m₂v_2i = m₁v_1f + m₂v_2f

Momentum is conserved…

in ANY collision → elastic OR inelastic as long as it is closed and isolated (no outside forces acting on it)

Elastic Collision

• KE of the system is conserved

  • total KE is unhanged

• both momentum & KE are conserved

• in a conserved & isolated system

• typically have 2 unknowns: solve equations simultaneously

• m₁v_1i + m₂v_2i = m₁v_1f + m₂v_2f

• ½ m₁v_1i² + ½ m₂v_2i² = ½ m₁v_1f² + ½ m₂v_2f²

What simpler equation can be used in place of the KE equation in elastic collision momentum conservation?

• v_1i - v_2i = -(v_1f - v_2f)

• or

• v_1i + v_1f = v_2i + v_2f

Newton’s Cradle is an example of…

• elastic collision

• momentum & kinetic energy are conserved

A 20-g bullet moving at 1000 m/s is fired through a 1-kg block of wood emerging at a speed of 100 m/s. If the block had been originally at rest and is free to move, what is its resulting speed?

Bullet

• m₁ = 20 g = 0.02 kg

• v_1i = 1000 m/s

• v_1f = 100 m/s

Block

• m₂ = 1 kg

• v_2i = 0 m/s

• v_2f = ?

• inelastic → momentum is conserved!!

• p_i = p_f

• m₁v_1i + m₂v_2i = m₁v_1f + m₂v_2f

• (0.02 kg)(1000 m/s) + (1 kg)(0 m/s) = (0.02 kg)(100 m/s) + (1 kg)(v_2f)

• 20 = 2 + v_2f

• v_2f = 18 m/s

Elastic vs. Inelastic Collision

• Elastic:

  • p_i = p_f

  • K_i = K_f

  • v_1i + v_1f = v_2i + v_2f

  • ex: billiard ball, gas molecules

• Inelastic:

  • p_i = p_f

  • K_i = K_f

    • KE not conserved

  • ex: car crash

Inelastic Collision

• some energy is transferred from kinetic energy to other forms (thermal, energy of sound, etc.) → KE is not conserved

• Includes perfectly inelastic collisions

Perfectly Inelastic Collisions

• objects stick together

• include all velocity directions and move with a common velocity after the collision

• the “after” collision combines the masses

• conservation of momentum becomes:

  • m₁v_1i + m₂v_2i = (m₁+ m₂)v_f

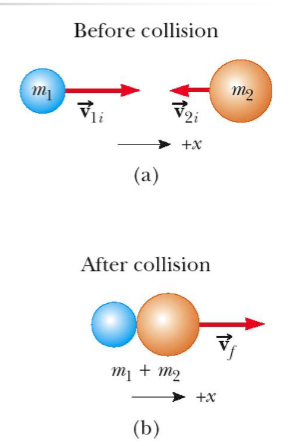
A 2500-kg truck moving at 10.00 m/s strikes a car waiting at a traffic light, hooking bumpers. the two continue to move together at 7.00 m/s. What was the mass of the struck car?

• m₁ = 2500 kg

• v_1i = 10 m/s

• m₂ = ?

• v_2i = 0 m/s

• v_f = 7 m/s

• perfectly inelastic collision

• m₁v_1i + m₂v_2i = (m₁+ m₂)v_f

• (2500 kg)(10 m/s) + (m₂)(0 m/s) = (2500 kg + m₂)(7 m/s)

• 25,000 = (2500 kg + m₂)(7 m/s)

• m₂ = 1071 kg

The ballistic pendulum was used to measure the speeds of the bullets before electronic timing devices were developed. The version shown in the figure consists of a large block of wood of mass M = 5.4 kg, hanging from two long cords. A bullet of mass m = 9.5 g is fired into the block, coming quickly to rest. The block + bullet then swing upward, their center of mass rising a vertical distance h = 6.3 cm before the pendulum comes momentarily to rest at the end of its arc. What is the speed of the bullet just prior to the collision?

• There are 2 events here. The bullet collides with the block. Then the bullet-block system swings upward by height h.

• Event 1: Inelastic Collision

  • In this event, the bullet embeds itself into the block, resulting in a perfectly inelastic collision where the total momentum before collision is conserved, but kinetic energy is not.

  • m₁v_1i + m₂v_2i = (m₁+ m₂)v_f

  • (0.0095 kg)(v_1i) + (5.4 kg)(0 m/s) = (5.4095 kg)(v_f)

• Event 2: The bullet-block system then rises to height h → energy is conserved in this event AFTER the collision

  • E_i = E_f

  • KE_i + PE_i = KE_f + PE_f

    • PE_i = 0

    • KE_f = 0

  • ½ (M + m)V² = (M + m)gh

  • ½ V² = gh

  • v = sqrt(2gh)

• Step 3: Plug In

• (0.0095 kg)(v_1i) + (5.4 kg)(0 m/s) = (5.4095 kg)(sqrt(2(9.8)(0.063 m)))

• v_1i = 632 m/s

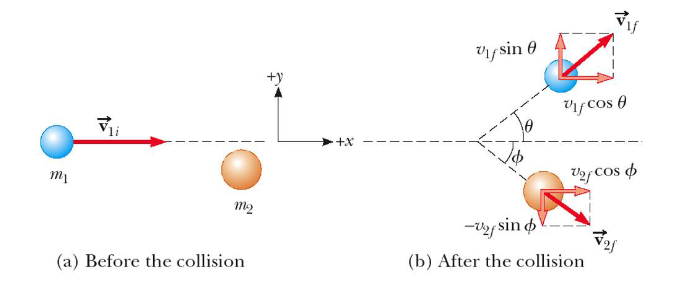
Glancing Collisions

• the “after” velocities have x & y components

• momentum is conserved in the x direction & y direction

  • apply conservation of momentum separately to each direction

  • the objects move at an angle to each other, resulting in different post-collision directions

Center of Mass

• the point that moves as though all of the system’s mass is concentrated there & all external forces are applied there

• location is important for stability

  • If we draw a line straight down from COM & it falls inside the base → it is in stable equilibrium and will balance

  • If it falls outside the base → it is unstable

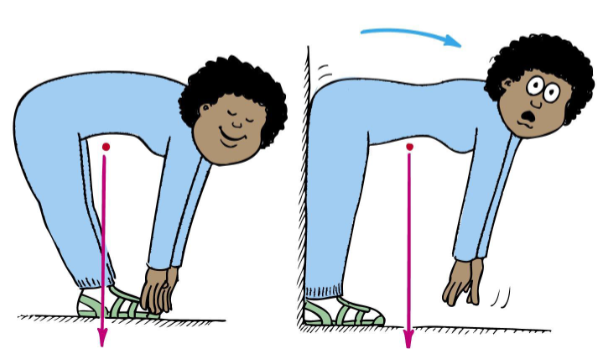
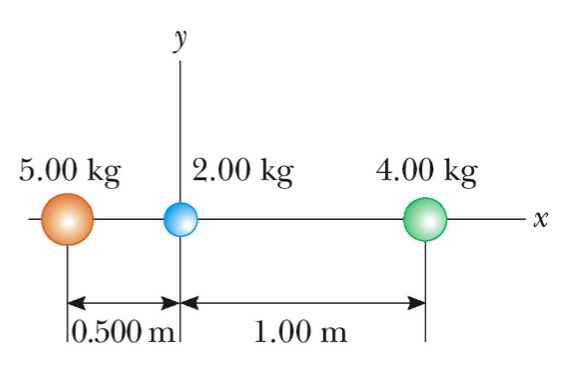
Where is the COM?

• x_com = (m1x1 + m2x2 + m3×3) / (m1 + m2 + m3)

• x_com = ((5)(0.5) + (2)(0) +(4)(1)) / (5 + 2 + 4) = 0.136 m

• Change in momentum = impulse = Δp

• Δp = FΔt

• mass changes acceleration, not Δp, so it is not relevant here

• A=D > B=C