Gravitational fields

Definition of a gravitational field:

It is the region around a body in which other bodies will feel a force due to the mass of the body

What are gravitational fields due to?

They are due to objects having mass

Definition of gravitational field strength

At any point in a gravitational field, the force acting per unit mass at that point (Nkg^-1)

How is mass normally modelled?

the mass of a spherical object as a point mass in its centre

what shows a greater gravitational field on a diagram

more densely packed field lines

equation for gravitational field strength

Gravitational field strength = gravitational force/ mass

g = F/m

units for gravitational field strength

(Nkg^-1)

gravitational force equation

F = -GMm/ r² where:

F = gravitational force

G = newtons gravitational constant

M or m = mass of each object

r = separation between (point masses of) the two objects

gravitational acceleration/ field strength equation

a = -GM/ r² (note we also see a as g)

Because:

F = -GMm/ r²

F=ma

ma = -GMm/ r² (cancel m)

a = -GM/ r²

close to the surface of the earth, what can we assume about the gravitational field?

That it’s uniform: represented by parallel lines, uniformly spaced and also always enter surface at 90 degrees.

Newtons law of gravitation

The gravitational force between two point masses is directly proportional to the product of their masses and inversely proportional to the square of their separation

Keplers 1st law 

Planets travel around the sun in elliptical orbits 

Keplers 2nd law

A line segment joining the sun to a planet will sweep out equal areas in equal times

Keplers 3rd law

The time period of the orbit squared is proportional to the mean radius of the orbit cubed: T² ∝ r³

And for bodies that move in a circular path, what does this become?

T² = (4π² / GM ) x r³

How else can we write the relationship between T² and r³

T² ∝ r³

T² = kr³

T²/ r³ = k (a constant)

T²₁/ r³₁ = T²₂/ r³₂

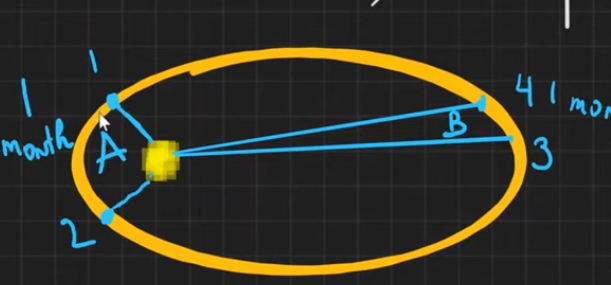
What happens to the planet in orbit around the sun when it is closer to the sun, near A? 

The planet speeds up, due to the fact its experiencing a greater gravitational force

Keplers third law proof 

To start derivation, remember gravitational force acts towards centre of rotation of planet.

F_g = F_c (gravitational force = centripetal force)

GMm / r² = mv²/ r (Cancel m)

Remember v = 2πr/ T

V² = 4π²/T²

GM / r² = (4π²r²/rT²)

T² = (4π²/GM) r³

What 3 things define a geostationary orbit?

1) They have an orbital period of 24 hours in the same direction as the rotation of the Earth 

2) They are in equatorial orbit 

Therefore:

3) They remain fixed in the sky to an observer on Earth  

How to calculate height of geostationary orbit

Height, we are finding r:

T² = (4π²/GM) r³

Radius of earth = 6400km

Mass of earth = 6 ×10²⁴ kg

r = cube root of T²GM / 4π² 

Plugging values in we get r = 4.23 × 10⁷ however this isn’t the distance from the surface of the earth, it’s the distance to the point mass (the centre of the earth). So we must do 4.23 × 10⁷ - 6400 ×10³ = 3.6 ×10⁷m

Definition of gravitational potential energy

The gravitational potential energy of a mass m (for a radial field around a point or spherical mass M) at a distance r from M is defined as:

Energy = -GMm / r ( unit is joules J )

Take note that its not over r²

Definition of gravitational potential 

The gravitational potential at a point in a gravitational field is the energy required to move a unit mass from infinity to that point in the field of the body of mass M 

V_g =  -GM/r 

The reason it is negative, as is the grav. potential energy, is because we define the gravitational potential energy as being equal to zero at infinity, so equation must be negative as work must be done on the body when moving it in the opposite direction to an attractive gravitational field, and as V_g at infinity is 0, V_g must be negative before it reaches infinity. 

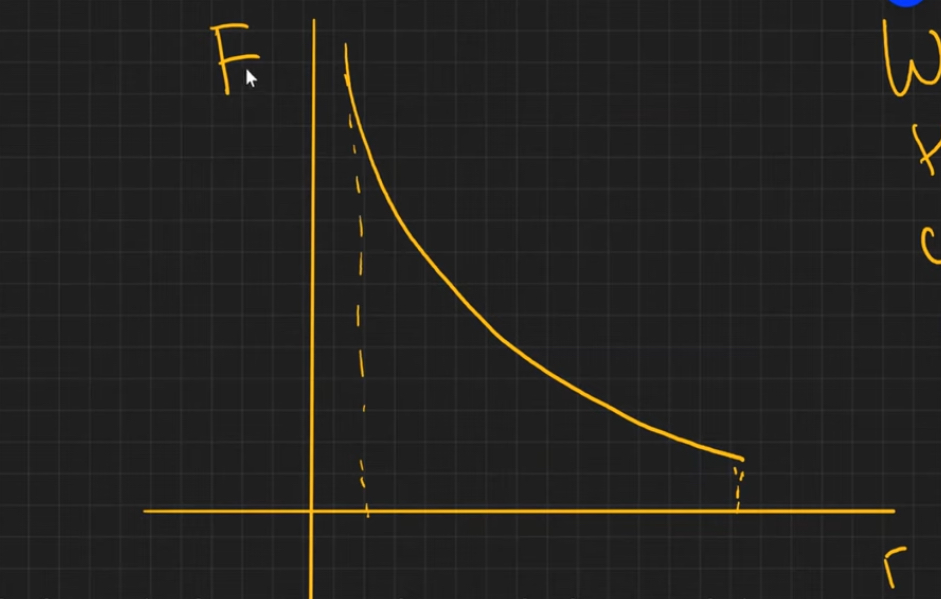
For a force-distance graph for a point or spherical mass, what does the area under the graph equal?

The work done 

Escape velocity of the earth 

The escape velocity from a point in a gravitational field is the minimum launch velocity required to move an object from that point to infinity 

How would we calculate the escape velocity?

Think about energy:

GPE must = KE

GMm/r = ½ mv²

v = (2GM/r)^1/2

Now sub in values we know for the earth.